Redoxgleichungen
Redoxgleichungen sind chemische Gleichungen von Redoxreaktionen. In Redoxreaktionen ändern sich die Oxidationszahlen der Atome, daher sind Kenntnisse der chemischen Nomenklatur und der Regeln zur Bestimmung von Oxidationszahlen eine wesentliche Voraussetzung für das erfolgreiche Lösen von Redoxgleichungen.
Reduktion ist der Vorgang, bei dem ein Atom seine Oxidationszahl verringert. Oxidation ist der Vorgang, bei dem ein Atom seine Oxidationszahl erhöht. Die Änderung der Oxidationszahl erfolgt durch die tatsächliche oder formale Abgabe von Elektronen (Oxidation) bzw. die Aufnahme von Elektronen (Reduktion; da Elektronen eine negative elektrische Ladung tragen, senkt ihre Aufnahme die Oxidationszahl).
Reduktionsmittel ist ein Reaktant, der die Reduktion eines anderen Reaktanten bewirkt (mindestens ein Atom des Reduktionsmittels erhöht seine Oxidationszahl). Oxidationsmittel ist ein Reaktant, der die Oxidation eines anderen Reaktanten verursacht (mindestens ein Atom des Oxidationsmittels verringert seine Oxidationszahl).
Halbgleichung beschreibt nur die Oxidation oder nur die Reduktion; in der Elektrochemie wird sie auch als Elektrodenreaktion bezeichnet.
Beim Lösen von Redoxgleichungen folgen wir allgemeinen Regeln zur Berechnung stöchiometrischer Koeffizienten nach folgendem Vorgehen:
- Bestimme die Oxidationszahlen aller Atome in der Gleichung.
- Schreibe die Halbgleichung für die Oxidation und die Halbgleichung für die Reduktion.
- Gleiche die Oxidations- und Reduktionshalbgleichungen rechnerisch so an, dass die Elektronenbilanz erfüllt ist.
- Addiere und passe beide Halbgleichungen an, um die vereinfachte Redoxgleichung (SRR) zu erhalten.
- Übertrage die erhaltenen Atomzahlen mithilfe stöchiometrischer Koeffizienten in die chemische Gleichung.
- Ordne gemäß der Atombilanzregel Stoffen, deren Atome ihre Oxidationszahl nicht geändert haben, stöchiometrische Koeffizienten zu.
- Handelt es sich um eine ionische Redoxgleichung, verwende zur Bestimmung stöchiometrischer Koeffizienten die Ladungsbilanz.
Einfache Disproportionierungs- und Komproportionierungs-Redoxreaktionen sind solche chemischen Reaktionen, bei denen sich die Oxidationszahl der Atome nur eines Elements ändert; ansonsten unterscheiden sie sich nicht von anderen Redoxreaktionen.
Redoxgleichungen, bei denen die Edukte Atome eines gegebenen Elements mit einer Oxidationszahl enthalten und die Produkte Atome desselben Elements mit unterschiedlichen Oxidationszahlen, nennt man Disproportionierungsgleichungen. Zum Beispiel:
3ReVIF6 + 10H2O → 2HReVIIO4 + ReIVO2 + 18HF
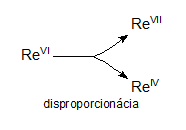
Redoxgleichungen, bei denen die Edukte Atome eines gegebenen Elements mit verschiedenen Oxidationszahlen enthalten und die Produkte Atome desselben Elements nur mit einer Oxidationszahl, nennt man Komproportionierungsgleichungen. Zum Beispiel:
NIVO2 + NIIO + 2NaOH → 2NaNIIIO2 + H2O
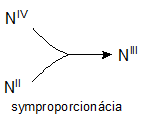
1. Gleichen Sie die Redoxgleichung aus:
Lösung:
Der erste Schritt besteht darin, die Oxidationszahlen der Atome in jeder Verbindung zu bestimmen:
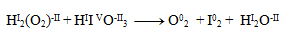
Damit ändern nur Iod und Sauerstoff ihre Oxidationszahlen. Für sie schreiben wir die Halbreaktionen, d. h. Reaktionen, die nur das betreffende oxidierende/reduzierende Element und Elektronen umfassen.
Oxidation:
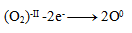
Reduktion:
2IIV +10e- -------> 2I0
Als Nächstes multiplizieren wir die Gleichungen so, dass die Elektronenzahl ausgeglichen ist:
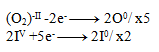
Und dann addieren wir die Gleichungen:
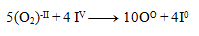
Wir setzen die erhaltenen Koeffizienten in die Ausgangsgleichung ein und berechnen die Anzahl der übrigen Atome, um dem Gesetz der Erhaltung der Atome desselben Elements zu genügen. Die resultierende Gleichung hat die Form:
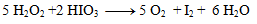
2.Ergänzen Sie die stöchiometrischen Koeffizienten in der Redoxgleichung:
Lösung:
Zunächst sind die Oxidationszahlen der Atome aller Edukte und Produkte zu bestimmen:
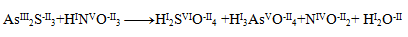
Wir erkennen, dass nur Arsen, Schwefel und Stickstoff ihre Oxidationszahlen ändern. Für diese Elemente schreiben wir Halbreaktionen, in denen wir auch die Zahl der ausgetauschten Elektronen angeben.
Oxidationsgleichungen:
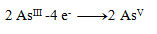
(ein Arsen benötigt 2 Elektronen)
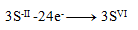
(ein Schwefel benötigt 8 Elektronen)
Reduktionsgleichung:
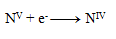
Der nächste Schritt ist, die Zahl der ausgetauschten Elektronen so anzupassen, dass in Oxidationen und Reduktionen dieselbe Anzahl übertragen wird – somit werden in allen drei Halbreaktionen 28 Elektronen ausgetauscht. 24+4=28 Elektronen in der Oxidation, also muss dasselbe in der Reduktion geschehen, daher:
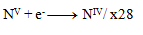
und damit
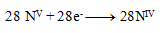
Die stöchiometrischen Koeffizienten aus den Halbreaktionen werden in die Gleichung übernommen und die übrigen Elemente berechnet. Die resultierende Gleichung hat die Form:
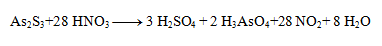
3. Gleichen Sie die folgenden Redoxgleichungen aus:
Lösung:
- a) 3,4,3,4,2
- b) 5,2,5,1,6
- c) 2,11,11,6,2,11,8
- d) 1,1,2,1,2,2
- e) 4,11,2,8
- f) 3,10,2,1,18
- g) 5,1,6,3,3
- h) 1,1,1,2
- i) 3,6,1,5,3
4.Bestimmen Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
Cr + H2SO4 → Cr2(SO4)3 + H2
Lösung:
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen von Chrom und Wasserstoff ändern:
Cr0 + HI2SVIO–II4 → CrIII2(SVIO–II4)3 + H02
Wir schreiben die Halbgleichungen für Oxidation und Reduktion:
Cr0 – 3e– → CrIII (Oxidation)
HI + 1e– → H0 (Reduktion)
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die zweite Halbgleichung mit drei:
Cr0 – 3e– → CrIII
3HI + 3e– → 3H0
Nun ist die Elektronenzahl ausgeglichen. Wir addieren die Halbgleichungen:
Cr0 – 3e– + 3HI + 3e– → CrIII + 3H0
Nach Vereinfachung:
Cr0 + 3HI → CrIII + 3H0
Dies stellt die vereinfachte Redoxgleichung (SRR) dar. Zur Gewinnung der stöchiometrischen Koeffizienten passen wir weiter an:
2Cr + 3H2SO4 → Cr2(SO4)3 + 3H2
5. Bestimmen Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
Lösung:
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen von Phosphor- und Kohlenstoffatomen ändern:
CaII3(PVO–II4)2 + SiIVO–II2 + C0 → P04 + CaIISiIVO–II3 + CIIO–II
Wir schreiben die Teilgleichungen für Oxidation und Reduktion:
C0 – 2e– → CII (Oxidation)
PV + 5e– → P0 (Reduktion)
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Teilgleichung mit fünf und die zweite mit zwei:
5C0 – 10e– → 5CII
2PV + 10e– → 2P0
Die Zahl der aufgenommenen und abgegebenen Elektronen ist identisch. Von hier an dürfen wir nur noch dieselben mathematischen Operationen auf beide Teilgleichungen gleichzeitig anwenden, sodass die Elektronenbilanz erhalten bleibt. Daher addieren wir beide Teilgleichungen und erhalten die Redoxgleichung:
5C0 – 10e– + 2PV + 10e– → 5CII + 2P0
nach Vereinfachung:
5C0 + 2PV → 5CII + 2P0
Die erhaltenen Zahlenwerte sind keine stöchiometrischen Koeffizienten, sondern geben die Anzahl der Atome an, die links und rechts der Gleichung vorhanden sein müssen. Auf der rechten Seite sollten laut Redoxgleichung zwei Phosphoratome mit der Oxidationszahl 0 stehen. Da diese als tetratomare Moleküle auftreten, wäre der stöchiometrische Koeffizient eine Bruchzahl. Deshalb multiplizieren wir die Redoxgleichung mit 2:
10C0 + 4PV → 10CII + 4P0
Auf der linken Seite der Gleichung müssen vier Phosphoratome vorhanden sein, daher setzen wir den Koeffizienten 2 vor Ca3(PO4)2. Auf der rechten Seite müssen ebenfalls vier Phosphoratome stehen, was bereits durch die tiefgestellte 4 in P4 gewährleistet ist, also hat diese Substanz den Koeffizienten 1:
2Ca3(PO4)2 + SiO2 + C → P4 + CaSiO3 + CO
Auf beiden Seiten der Gleichung müssen zehn Kohlenstoffatome vorhanden sein. Daher setzen wir den Koeffizienten 10 vor C und ebenso vor CO:
2Ca3(PO4)2 + SiO2 + 10C → P4 + CaSiO3 + 10CO
Es fehlen noch Koeffizienten vor SiO2 und CaSiO3. Auf der linken Seite haben wir 6 Calciumatome, daher setzen wir den Koeffizienten 6 vor CaSiO3. Das bedeutet, dass wir links auch 6 Siliciumatome benötigen, also setzen wir den Koeffizienten 6 vor SiO2.
2Ca3(PO4)2 + 6SiO2 + 10C → P4 + 6CaSiO3 + 10CO
Auf diese Weise erhielten alle Stoffe in der chemischen Gleichung ihre stöchiometrischen Koeffizienten. Wir prüfen die Lösung durch Zählen der Sauerstoffatome auf beiden Seiten der Gleichung (28 = 28). Da die erhaltenen stöchiometrischen Koeffizienten (2, 6, 10 = 1, 6, 10) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
6.Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
MnO4– + Fe2+ + H3O+ → Mn2+ + Fe3+ + H2O
Lösung:
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen der Mangan- und Eisenatome ändern:
(MnVIIO–II4)– + Fe2+ + (HI3O–II)+ → Mn2+ + Fe3+ + HI2O–II
Wir schreiben die Halbreaktionen von Oxidation und Reduktion (die Oxidationszahl einatomiger Ionen ist identisch mit ihrer Ladungszahl):
Fe2+ – e– → Fe3+ (Oxidation)
MnVII + 5e– → MnII (Reduktion)
Da die Zahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Halbreaktion mit fünf und addieren beide Halbreaktionen:
5Fe2+ – 5e– → 5Fe3+
MnVII + 5e– → MnII
5Fe2+ – 5e– + MnVII + 5e– → 5Fe3+ + MnII
Nach Anpassung erhalten wir die Redoxreaktion:
5Fe2+ + MnVII → 5Fe3+ + MnII
Die erhaltenen Zahlenwerte geben die Anzahl der Atome an, die auf beiden Seiten der chemischen Gleichung vorhanden sein müssen. Da fünf Eisenatome auf beiden Seiten stehen müssen, setzen wir den Koeffizienten 5 vor die Ionen Fe2+ und Fe3+.
MnO4– + 5Fe2+ + H3O+ → Mn2+ + 5Fe3+ + H2O
Der Koeffizient von MnO4– und Mn2+ muss 1 sein, was bereits erfüllt ist. Zwei Stoffe bleiben ohne Koeffizienten: als Edukt das Oxonium-Kation und als Produkt Wasser. Da es sich um eine ionische Gleichung handelt, verwenden wir die Regel der Ladungsbilanz. Auf der rechten Seite der Gleichung haben alle Ionen bereits Koeffizienten; die Summe der Ladungszahlen rechts beträgt 1·2 + 5·3 + 1·0 = 17. Links muss ebenfalls die Summe der Ladungszahlen 17 betragen; bislang haben wir (außer H3O+): 1·(–1) + 5·2 = 9. Diese Summe muss um 8 erhöht werden, daher ist der Koeffizient vor H3O+ gleich 8:
MnO4– + 5Fe2+ + 8H3O+ → Mn2+ + 5Fe3+ + H2O
(Zur Berechnung des stöchiometrischen Koeffizienten für H3O+ könnte man auch die Ladungsbilanz in Form einer Gleichung verwenden, wobei der Koeffizient für H2O als y und der für H3O+ als x bezeichnet wird. Es gilt: 1·(–1) + 5·2 + x·1 = 1·2 + 5·3 + y·0. Daraus folgt x = 8.)
Auf der linken Seite stehen 8·3 = 24 Wasserstoffatome, daher setzen wir rechts den Koeffizienten 12 vor H2O:
MnO4– + 5Fe2+ + 8H3O+ → Mn2+ + 5Fe3+ + 12H2O
Mit diesem Vorgehen erhielten wir stöchiometrische Koeffizienten für alle Stoffe der chemischen Gleichung. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten der Gleichung zählen (12 = 12). Da die erhaltenen stöchiometrischen Koeffizienten (1, 5, 8 = 1, 5, 12) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
7. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
Cu + HNO3 → Cu(NO3)2 + NO2 + H2O
Lösung:
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen von Kupfer und Stickstoff ändern:
Cu0 + HINVO–II3 → CuII(NVO–II3)2 + NIVO–II2 + HI2O–II
Wir schreiben die Teil-(Halb-)Reaktionen für Oxidation und Reduktion:
Cu0 – 2e– → CuII (Oxidation)
NV + e– → NIV (Reduktion)
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die zweite Halbreaktion mit zwei und addieren beide Halbreaktionen:
Cu0 – 2e– → CuII
2NV + 2e– → 2NIV
Cu0 – 2e– + 2NV + 2e– → CuII +2NIV
und nach Vereinfachung erhalten wir die SRR:
Cu0 + 2NV → CuII +2NIV
Die erhaltenen Zahlenwerte sind nicht die stöchiometrischen Koeffizienten, sondern geben die Anzahl der Atome an, die links und rechts der chemischen Gleichung auftreten müssen. Auf beiden Seiten muss ein Kupferatom vorhanden sein, daher ist der Koeffizient vor Cu und Cu(NO3)2 gleich 1. Auf der rechten Seite müssen zwei Stickstoffatome mit Oxidationszahl IV vorhanden sein, deshalb setzen wir den Koeffizienten 2 vor NO2:
Cu + HNO3 → Cu(NO3)2 + 2NO2 + H2O
Auf der linken Seite müssen zwei Stickstoffatome mit Oxidationszahl V stehen, doch wir können nicht den Koeffizienten 2 vor HNO3 setzen, weil nicht alle Stickstoffatome am Redoxprozess teilnehmen. Auch auf der rechten Seite gibt es Stickstoffatome mit unveränderter Oxidationszahl – in Cu(NO3)2. Daher muss der stöchiometrische Koeffizient vor HNO3 größer sein als der aus den Teilreaktionen erhaltene. Dieser Koeffizient muss sowohl den Redox- als auch den Nicht-Redox-Anteil berücksichtigen. Vor Cu(NO3)2 steht bereits der Koeffizient 1, der zwei Stickstoffatome mit Oxidationszahl V enthält. Daher setzen wir den Koeffizienten 4 vor HNO3: Zwei Stickstoffatome nahmen am Redoxprozess teil, zwei änderten ihre Oxidationszahl nicht:
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + H2O
Die letzte Substanz ohne stöchiometrischen Koeffizienten ist Wasser. Auf der linken Seite haben wir 4 Wasserstoffatome, daher setzen wir den Koeffizienten 2 vor H2O:
Cu + 4HNO3 → Cu(NO3)2 + 2NO2 + 2H2O
Auf diese Weise erhielten wir die stöchiometrischen Koeffizienten für alle Stoffe in der chemischen Gleichung. Wir prüfen die Lösung durch Zählen der Sauerstoffatome auf beiden Seiten der Gleichung (12 = 12). Da die erhaltenen stöchiometrischen Koeffizienten (1, 4 = 1, 2, 2) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
8. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
KMnO4 + HBr → Br2 + MnBr2 + KBr + H2O
Lösung:
|
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen von Mangan und Brom ändern:
Br02 + MnIIBr–I 2 + KIBr–I + H2O–II
Wir schreiben die Teil-(Halb-)Reaktionen für Oxidation und Reduktion:
Br0 (Oxidation)
MnII (Reduktion)
Da die Zahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Halbreaktion mit fünf und addieren die Teilreaktionen:
5Br0
MnII
5Br–I – 5e– + MnVII + 5e–= 5Br0 + MnII
und nach Vereinfachung erhalten wir die SRR:
5Br0 + MnII
Auf der rechten Seite der Gleichung müssen gemäß SRR fünf Bromatome mit der Oxidationszahl 0 stehen. Da Brom als zweiatomiges Molekül vorkommt, wäre der stöchiometrische Koeffizient eine Bruchzahl. Daher multiplizieren wir die SRR mit 2:
10Br–I + 2MnVII → 10Br0 + 2MnII
Die erhaltenen Zahlen sind nicht die stöchiometrischen Koeffizienten, sondern geben die Anzahl der Atome an, die links und rechts vorhanden sein müssen. Auf beiden Seiten müssen zwei Mangantome stehen, daher ist der Koeffizient vor KMnO4 und MnBr2 gleich 2:
2KMnO4 + HBr → Br2 + 2MnBr2 + KBr + H2O
Zugleich müssen auf der linken Seite zehn Bromatome mit Oxidationszahl –I stehen, doch wir können nicht den Koeffizienten 10 vor HBr setzen, da rechts Brom auch mit unveränderter Oxidationszahl –I vorkommt. Somit muss der Koeffizient vor HBr größer als 10 sein. Rechts müssen 10 Bromatome mit Oxidationszahl 0 stehen, daher setzen wir den Koeffizienten 5 vor Br2:
2KMnO4 + HBr → 5Br2 + 2MnBr2 + KBr + H2O
Auf der linken Seite haben wir zwei Kaliumatome, daher setzen wir den Koeffizienten 2 vor KBr:
2KMnO4 + HBr → 5Br2 + 2MnBr2 + 2KBr + H2O
Da nun rechts vor allen bromhaltigen Stoffen Koeffizienten stehen, befinden sich dort 16 Bromatome; folglich setzen wir den Koeffizienten 16 vor HBr:
2KMnO4 + 16HBr → 5Br2 + 2MnBr2 + 2KBr + H2O
Der Koeffizient 16 vor HBr bedeutet auch, dass 10 Bromatome am Redoxprozess beteiligt waren und die restlichen sechs unverändert blieben. Auf der linken Seite stehen außerdem 16 Wasserstoffatome, daher setzen wir rechts den Koeffizienten 8 vor H2O:
→ 5Br2 + 2MnBr2 + 2KBr + 8H2O
So erhielten wir die stöchiometrischen Koeffizienten für alle Stoffe in der chemischen Gleichung. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten zählen (8 = 8). Da die erhaltenen stöchiometrischen Koeffizienten (2, 16 = 5, 2, 2, 8) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
|
9. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
ReF6 + H2O → HReO4 + ReO2 + HF
Lösung:
|
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich nur die Oxidationszahl des Rheniumatoms ändert:
ReVIF–I6 + HI2O–II → HIReVIIO–II4 + ReIVO–II2 + HIF–I
Dies ist eine Disproportionierungsgleichung. Wir schreiben die Teil-(Halb-)Reaktionen für Oxidation und Reduktion:
ReVII (Oxidation)
→ ReIV (Reduktion)
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Halbreaktion mit zwei und addieren die Teilreaktionen:
2ReVI – 2e– → 2ReVII
ReVI + 2e– → ReIV
2ReVI – 2e– + ReVI + 2e– = 2ReVII + ReIV
Nach Vereinfachung erhalten wir die SRR:
2ReVII + ReIV
Aus der SRR folgt, dass links drei Rheniumatome mit Oxidationszahl VI und rechts zwei Rheniumatome mit Oxidationszahl VII sowie ein Atom mit Oxidationszahl IV vorhanden sein müssen. Wir fügen der Redoxgleichung stöchiometrische Koeffizienten hinzu:
3ReF6 + H2O → 2HReO4 + ReO2 + HF
Links stehen 18 Fluoratome, daher setzen wir den Koeffizienten 18 vor HF:
3ReF6 + H2O → 2HReO4 + ReO2 + 18HF
Die einzige Substanz ohne stöchiometrischen Koeffizienten ist Wasser. Auf der rechten Seite stehen 2 + 18 = 20 Wasserstoffatome, daher setzen wir den Koeffizienten 10 vor H2O:
2HReO4 + ReO2 + 18HF
|
Auf diese Weise erhielten alle Stoffe in der chemischen Gleichung ihre stöchiometrischen Koeffizienten. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten der Gleichung zählen (10 = 10). Da die erhaltenen stöchiometrischen Koeffizienten (3, 10 = 2, 1, 18) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
10.Bestimmen Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
MnO42– + H3O+ → MnO4– + MnO2 + H2O
Lösung:
|
Berechnen Sie die Oxidationszahlen aller Atome. Wir stellen fest, dass sich nur die Oxidationszahl des Manganatoms ändert:
(MnVIO–II4)2– + (HI3O–II)+ → (MnVIIO–II4)– + MnIVO–II2 + HI2O–II
Dies ist eine Disproportionierungsgleichung. Wir schreiben die Teilgleichungen für Oxidation und Reduktion:
MnVI – 1e– → MnVII (Oxidation)
MnVI + 2e– → MnIV (Reduktion)
Da die Zahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Teilgleichung mit zwei und addieren die Teilgleichungen:
2MnVI – 2e– → 2MnVII
<>MnVI + 2e– → MnIV
2MnVI – 2e– + MnVI + 2e– → 2MnVII + MnIV
und nach Anpassung erhalten wir das Nettoladungsergebnis:
→ 2MnVII + MnIV
Daraus folgt, dass auf der linken Seite drei Mangantome mit Oxidationszahl VI und auf der rechten Seite zwei Mangantome mit Oxidationszahl VII sowie ein Atom mit Oxidationszahl IV stehen müssen. Wir fügen der Redoxgleichung stöchiometrische Koeffizienten hinzu:
3MnO42– + H3O+ → 2MnO4– + MnO2 + H2O
Zwei Spezies in der Gleichung bleiben ohne Koeffizienten: das Edukt – das Oxonium-Kation – und das Produkt – Wasser. Da es sich um eine ionische Gleichung handelt, verwenden wir die Ladungsbilanz. Rechts hat nur ein Ion einen Koeffizienten, daher können wir die Ladesumme berechnen: 2 · (–1) + 1 · 0 + 1 · 0 = –2. Links muss ebenfalls die Gesamtladung –2 sein, derzeit haben wir (ohne H3O+): 3 · (–2) = –6. Wir müssen diese Summe um 4 erhöhen, also ist der Koeffizient vor H3O+ gleich 4:
3MnO42– + 4H3O+ → 2MnO4– + MnO2 + H2O
Links haben wir 12 Wasserstoffatome, daher setzen wir den Koeffizienten 6 vor H2O:
3MnO42– + 4H3O+ → 2MnO4– + MnO2 + 6H2O
|
Mit diesem Verfahren erhalten alle Stoffe in der chemischen Gleichung ihre stöchiometrischen Koeffizienten. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten der Gleichung zählen (16 = 16). Da die erhaltenen stöchiometrischen Koeffizienten (3, 4 = 2, 1, 6) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
11. Bestimmen Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
NO2 + NO + NaOH → NaNO2 + H2O
Lösung:
|
Berechnen Sie die Oxidationszahlen aller Atome. Wir stellen fest, dass sich nur die Oxidationszahl des Stickstoffatoms ändert; wir unterstreichen seine Symbole:
NIVO–II2 + NIIO–II + NaIO–IIHI → NaINIIIO–II2 + HI2O–II
Dies ist eine Komproportionierungsgleichung. Wir schreiben die Teilgleichungen für Oxidation und Reduktion:
NII – 1e– → NIII (Oxidation)
NIV + 1e– → NIII (Reduktion)
Da die Zahl der aufgenommenen und abgegebenen Elektronen bereits gleich ist, addieren wir die Teilgleichungen:
NIII
→ NIII
NII – 1e– + NIV + 1e– →NIII + NIII
und nach Anpassung erhalten wir die Netto-Atomausgleichsrelation (ARR):
NII + NIV → 2NIII
Daraus folgt, dass auf der rechten Seite zwei Stickstoffatome mit der Oxidationszahl III stehen müssen und auf der linken Seite je eines mit II und eines mit IV. Wir fügen der Redoxgleichung stöchiometrische Koeffizienten hinzu:
NO2 + NO + NaOH → 2NaNO2 + H2O
Auf der rechten Seite befinden sich zwei Natriumatome, daher setzen wir den Koeffizienten 2 vor NaOH:
NO2 + NO + 2NaOH → 2NaNO2 + H2O
Die einzige Substanz ohne stöchiometrischen Koeffizienten ist Wasser. Links haben wir 2 Wasserstoffatome, daher muss der Koeffizient vor H2O gleich 1 sein:
NO2 + NO + 2NaOH → 2NaNO2 + H2O
|
Mit diesem Verfahren erhalten alle Stoffe in der chemischen Gleichung ihre stöchiometrischen Koeffizienten. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten zählen (5 = 5). Da die erhaltenen Koeffizienten (1, 1, 2 = 2, 1) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
12. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung:
I– + IO3– + H3O+ → I2 + H2O
Lösung:
|
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich nur die Oxidationszahlen der Iodatome ändern; wir unterstreichen ihre Symbole:
→ I02 + HI2O–II
Dies ist eine Symproportionierungs- (Komproportionierungs-)Gleichung. Wir schreiben die Halbreaktionen für Oxidation und Reduktion:
→ I0 (Oxidation)
IV + 5e– → I0 (Reduktion)
Da die Zahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Halbreaktion mit fünf und addieren die Halbreaktionen:
5I–I – 5e– → 5I0
IV + 5e– → I0
5I–I – 5e– + IV + 5e– → 5I0 + I0
Nach Vereinfachung erhalten wir die Netto-Atomausgleichsrelation (ARR):
5I–I + IV → 6I0
Die erhaltenen Zahlenwerte sind nicht die stöchiometrischen Koeffizienten, sondern geben die Anzahl der Atome an, die links und rechts der chemischen Gleichung auftreten müssen. Aus der ARR folgt, dass die linke Seite fünf Iodatome mit der Oxidationszahl –I enthalten muss, daher setzen wir den Koeffizienten 5 vor I–. Zudem muss links ein Iodatom mit der Oxidationszahl V vorhanden sein, also ist der Koeffizient vor IO3– gleich 1. Rechts müssen sechs Iodatome mit Oxidationszahl 0 stehen, daher setzen wir den Koeffizienten 3 vor I2:
5I– + IO3– + H3O+ → 3I2 + H2O
Zwei Spezies in der Gleichung fehlen noch Koeffizienten: das Oxonium-Kation als Edukt und Wasser als Produkt. Da es sich um eine ionische Gleichung handelt, verwenden wir die Regel der Ladungsbilanz. Rechts gibt es keine Ionen, also ist die Ladesumme rechts null. Links muss die gleiche Gesamtladung vorliegen. Bisher (ohne H3O+) haben wir 5·(–1) + 1·(–1) = –6. Wir müssen diese Summe um +6 erhöhen, daher ist der Koeffizient vor H3O+ gleich 6:
5I– + IO3– + 6H3O+ → 3I2 + H2O
Links befinden sich 18 Wasserstoffatome, daher setzen wir den Koeffizienten 9 vor H2O:
5I– + IO3– + 6H3O+ → 3I2 + 9H2O
Mit diesem Verfahren erhielten wir die stöchiometrischen Koeffizienten für alle Spezies in der chemischen Gleichung. Wir prüfen die Lösung durch Zählen der Sauerstoffatome auf beiden Seiten (9 = 9). Da die erhaltenen Koeffizienten (5, 1, 6 = 3, 9) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen der chemischen Gleichung abgeschlossen.
|
13. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung (Anspruchsvollere Aufgabe für die Chemie-Olympiade):
Lösung:
|
Wir berechnen die Oxidationszahlen aller Atome. Wir stellen fest, dass sich die Oxidationszahlen aller Atome ändern: Eisen, Schwefel und Sauerstoff:
FeIIS–I2 + O02 → FeIII2O–II3 + SIVO–II2
Wir schreiben die Halbreaktionen für Oxidation und Reduktion:
FeII – 1e– → FeIII (Oxidation)
S–I – 5e– → SIV (Oxidation)
O0 + 2e– → O–II (Reduktion)
Da Eisen und Schwefel links in derselben Verbindung auftreten, muss ihr Verhältnis gemäß den stöchiometrischen Indizes erhalten bleiben. Deshalb multiplizieren wir die erste Halbreaktion mit eins, die zweite mit zwei und addieren:
FeII – 1e– → FeIII
2S–I – 10e– → 2SIV
FeII – 1e– + 2S–I – 10e– → FeIII + 2SIV
Nach Anpassung erhalten wir die kombinierte Halbreaktion:
FeII + 2S–I – 11e– → FeIII + 2SIV
Diese kombinierte Halbreaktion gleichen wir nun zusammen mit der Halbreaktion für Sauerstoff ab:
FeII + 2S–I – 11e– → FeIII + 2SIV
O0 + 2e– →O–II
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste kombinierte Halbreaktion mit 2 und die Sauerstoff-Halbreaktion mit 11 und addieren:
2FeII + 4S–I – 22e– → 2FeIII + 4SIV
11O0 + 22e– → 11O–II
2FeII + 4S–I – 22e– + 11O0 + 22e– → 2FeIII + 4SIV + 11O–II
Nach Vereinfachung erhalten wir die ARR:
2FeII + 4S–I + 11O0 → 2FeIII + 4SIV + 11O–II
Links müssen elf Sauerstoffatome mit Oxidationszahl 0 vorhanden sein. Da Sauerstoff als zweiatomiges Molekül vorkommt, wäre der stöchiometrische Koeffizient eine Bruchzahl. Deshalb multiplizieren wir die ARR mit 2:
4FeII + 8S–I + 22O0 → 4FeIII + 8SIV + 22O–II
Links sollten 4 Eisen- und 8 Schwefelatome stehen, daher setzen wir den Koeffizienten 4 vor FeS2. Außerdem benötigen wir links 22 Sauerstoffatome, daher setzen wir den Koeffizienten 11 vor O2:
4FeS2 + 11O2 → Fe2O3 + SO2
Rechts müssen ebenfalls vier Eisen- und acht Schwefelatome stehen, daher setzen wir den Koeffizienten 2 vor Fe2O3 und den Koeffizienten 8 vor SO2:
4FeS2 + 11O2 → 2Fe2O3 + 8SO2
Mit diesem Verfahren erhielten wir die stöchiometrischen Koeffizienten für alle Spezies in der chemischen Gleichung. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten zählen (22 = 22). Da die Koeffizienten (4, 11 = 2, 8) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen abgeschlossen.
|
14. Finden Sie die stöchiometrischen Koeffizienten in der folgenden chemischen Gleichung (Anspruchsvollere Aufgabe für die Chemie-Olympiade):
Au + KCN + O2 + H2O → K[Au(CN)2] + KOH
Lösung:
|
Wir berechnen die Oxidationszahlen aller Atome. Da das Cyanid-Anion während der Reaktion im Wesentlichen unverändert bleibt (nur koordiniert wird), müssen die Oxidationszahlen von Kohlenstoff und Stickstoff nicht separat bestimmt werden; es genügt, die Ladung des gesamten CN–-Anions zu berücksichtigen. Wir stellen fest, dass sich die Oxidationszahlen von Gold und Sauerstoff ändern.
Au0 + KICN– + O02 + HI2O–II → KI[AuI(CN–)2] + KIO–IIHI
Wir schreiben die Halbreaktionen für Oxidation und Reduktion:
Au0 – 1e– → AuI (Oxidation)
O0 + 2e– → O–II (Reduktion)
Da die Anzahl der aufgenommenen und abgegebenen Elektronen gleich sein muss, multiplizieren wir die erste Halbreaktion mit zwei und addieren die Halbreaktionen:
2Au0 – 2e– → 2AuI
O0 + 2e– → O–II
2Au0 – 2e– + O0 + 2e– → 2AuI + O–II
und nach Vereinfachung erhalten wir die ARR:
2Au0 + O0 → 2AuI + O–II
Links müssen zwei Sauerstoffatome im Oxidationszustand 0 stehen, Sauerstoff ist jedoch zweiatomig, daher wäre der stöchiometrische Koeffizient eine Bruchzahl. Wir multiplizieren die ARR daher mit 2:
4Au0 + 2O0 → 4AuI + 2O–II
Die erhaltenen Zahlen geben die Anzahl der Atome an, die links und rechts vorhanden sein müssen. Auf beiden Seiten müssen vier Goldatome stehen, daher ist der Koeffizient vor Au und vor K[Au(CN)2] gleich 4.
4Au + KCN + O2 + H2O → 4K[Au(CN)2] + KOH
Auch links müssen zwei Sauerstoffatome im Oxidationszustand 0 stehen, was mit dem Koeffizienten 1 vor O2 bereits erfüllt ist. Wir können rechts nicht den Koeffizienten 2 vor KOH setzen, weil es nicht nur die am Redoxprozess beteiligten Sauerstoffatome enthält, sondern auch jene aus dem Edukt Wasser. Da rechts acht Cyanid-Anionen vorliegen, setzen wir den Koeffizienten 8 vor KCN:
4Au + 8KCN + O2 + H2O → 4K[Au(CN)2] + KOH
Links befinden sich acht Kaliumatome; rechts sind vier Kaliumatome in 4K[Au(CN)2] gebunden, daher setzen wir den Koeffizienten 4 vor KOH:
4Au + 8KCN + O2 + H2O → 4K[Au(CN)2] + 4KOH
Die letzte Spezies ohne stöchiometrischen Koeffizienten ist Wasser. Da rechts vier Wasserstoffatome stehen, setzen wir links den Koeffizienten 2 vor H2O:
4Au + 8KCN + O2 + 2H2O → 4K[Au(CN)2] + 4KOH
Mit diesem Verfahren erhielten wir die stöchiometrischen Koeffizienten für alle Spezies in der chemischen Gleichung. Wir prüfen die Lösung, indem wir die Sauerstoffatome auf beiden Seiten zählen (4 = 4). Da die Koeffizienten (4, 8, 1, 2 = 4, 4) keinen gemeinsamen Teiler außer 1 besitzen, ist das Ausgleichen abgeschlossen.
|