sk|cz|en|

Physik

Bewegungen in einem homogenen Gravitationsfeld

1.Charakterisieren Sie die Bewegungen im homogenen Gravitationsfeld der Erde.

Lösung:

Das Gravitationsfeld, das sich bis in eine geringe Höhe über der Erdoberfläche erstreckt (h << RZ), kann als homogen betrachtet werden. Ein solches Feld hat an jedem Punkt im Raum die gleichen Werte physikalischer Größen. Neben dem freien Fall gehören dazu der vertikale Wurf nach oben, der horizontale Wurf und der schiefe (Projektil-)Wurf nach oben.

Lage des Körpers zur Zeit t | Maximalwerte

Freier Fall
v=gt,    s=gt22v = g t, \quad s = \frac{g t^2}{2}

Vertikaler Wurf nach oben
v=v0−gt,s=v0t−gt22v = v_0 - g t, \quad s = v_0 t - \frac{g t^2}{2}

t=v0g,h=v022gt = \frac{v_0}{g}, \quad h = \frac{v_0^2}{2g}

Horizontaler Wurf
x=v0t,y=h−gt22x = v_0 t, \quad y = h - \frac{g t^2}{2}

v2=v02+(gt)2v^2 = v_0^2 + (g t)^2

t=2hg,d=v02hgt = \sqrt{\frac{2h}{g}}, \quad d = v_0 \sqrt{\frac{2h}{g}}

Schiefer Wurf nach oben
x=v0tcos⁡αx = v_0 t \cos \alpha 

y=v0tsin⁡α−gt22y = v_0 t \sin \alpha - \frac{g t^2}{2}

t=2v0sin⁡αg,h=v02sin⁡2α2gt = \frac{2 v_0 \sin \alpha}{g}, \quad h = \frac{v_0^2 \sin^2 \alpha}{2g}

d=v02sin⁡2αgd = \frac{v_0^2 \sin 2\alpha}{g}


2.Ein Körper fällt aus einer Höhe von 60 m. Gleichzeitig wird ein anderer Körper vom Boden aus mit der Anfangsgeschwindigkeit v0 = 120 m·s-1 vertikal nach oben geworfen. Nach welcher Zeit und in welcher Höhe über dem Boden treffen sich die beiden Körper?

Lösung:

Analyse:

h = 60 m, v0 = 120 m·s-1

h1 + h2 = h

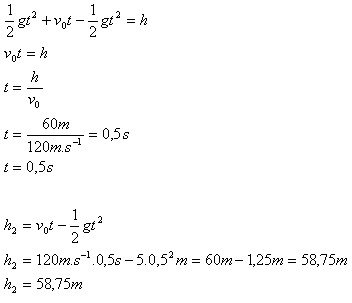
fyzika-pohyby-v-homogennom-gravitacnom-poli-2.gif

Die Körper treffen sich nach 0,5 s in einer Höhe von 58,75 m über dem Boden.

3.Ein frei fallender Stein hat an einem Punkt seiner Bahn die Momentangeschwindigkeit 50 m·s-1 und an einem anderen, tiefer gelegenen Punkt 80 m·s-1. Wie lange dauert es, bis der Stein vom ersten zum zweiten Punkt fällt, und wie weit liegen die beiden Punkte auseinander?

Lösung:

Analyse:

v1 = 50 m·s-1, v2 = 80 m·s-1

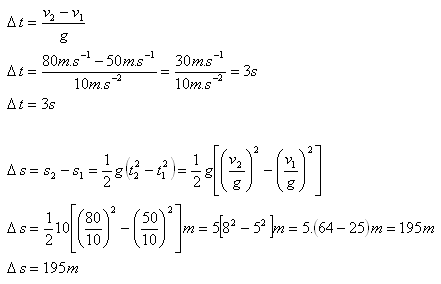
fyzika-pohyby-v-homogennom-gravitacnom-poli-3.gif 

Der Stein fällt in 3 s vom ersten zum zweiten Punkt. Der Abstand zwischen den Punkten beträgt 195 m.

4.Mit welcher Geschwindigkeit tritt der Wasserstrahl aus der Fontänendüse aus, wenn das Wasser eine Höhe von 20 m erreicht?

Lösung:

Analyse:

h = 20 m, v = ?

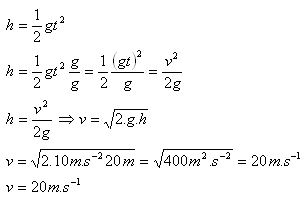
fyzika-pohyby-v-homogennom-gravitacnom-poli-4.gif 

Das Wasser tritt mit einer Geschwindigkeit von v = 20 m·s-1 aus der Fontäne aus.

5.Ein Ball, der vertikal nach oben geworfen wurde, kehrte nach 2 s zum Abwurfpunkt zurück. Welche Höhe erreichte er?

Lösung:

Analyse:

2t = 2 s

t = 1 s — die Aufstiegszeit des Balls

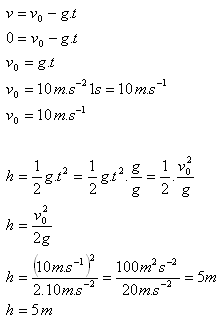
fyzika-pohyby-v-homogennom-gravitacnom-poli-5.gif

Der Ball stieg auf eine Höhe von 5 m.

6.Aus dem Fenster eines Hochhauses warf ein Junge einen Tennisball horizontal; er landete nach 3 Sekunden in einer Entfernung von 15 m vom Gebäude. Bestimmen Sie die Höhe des Fensters über dem Boden und die Anfangsgeschwindigkeit des Balls.

Lösung:

Analyse:

d = 15 m, t = 3 s

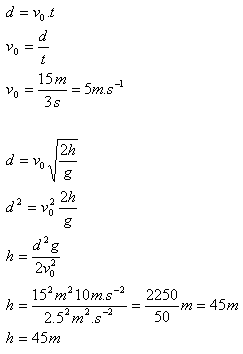
fyzika-pohyby-v-homogennom-gravitacnom-poli-6.gif 

Die Anfangsgeschwindigkeit des Balls beträgt 5 m·s-1. Die Höhe des Fensters über dem Boden beträgt 45 m.

7.Ein Flugzeug lässt eine Bombe auf ein Schiff fallen. Das Flugzeug fliegt in einer Höhe von 320 m über dem Meer mit einer Geschwindigkeit von 180 km·h-1. Das Schiff bewegt sich mit 36 km·h-1. In welchem Abstand vom Schiff muss die Besatzung die Bombe ausklinken, damit sie das Schiff trifft, wenn sich das Flugzeug

  • a) in gleicher Richtung wie das Schiff bewegt
  • b) in entgegengesetzter Richtung zum Schiff bewegt

Lösung:

Analyse:

v1 = 180 km·h-1 = 50 m·s-1, v2 = 36 km·h-1 = 10 m·s-1, h = 320 m

fyzika-pohyby-v-homogennom-gravitacnom-poli-7.gif 

  • a) Das Flugzeug fliegt in gleicher Richtung wie das Schiff: x = d – s = 400 m − 80 m = 320 m vor dem Schiff
  • b) Das Flugzeug fliegt in entgegengesetzter Richtung: y = d + s = 400 m + 80 m = 480 m vor dem Schiff

8.Ein Kugelstoßer warf die Kugel schräg nach oben mit einer Anfangsgeschwindigkeit von 10 m·s-1. Vergleichen Sie die Wurfweiten für die Höhenwinkel 30o, 45o, 60o.

Lösung:

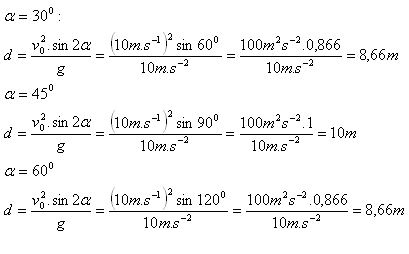
fyzika-pohyby-v-homogennom-gravitacnom-poli-8.gif

Die Entfernungen sind nur theoretisch und vernachlässigen den Luftwiderstand.

9.Ein Körper wurde schräg nach oben mit der Anfangsgeschwindigkeit v0 = 30 m·s-1 unter einem Höhenwinkel von 50o geworfen.

  • a) Bestimmen Sie seine Lage zur Zeit t = 1,5 s.
  • b) Welche maximale Höhe erreicht er?

Lösung:

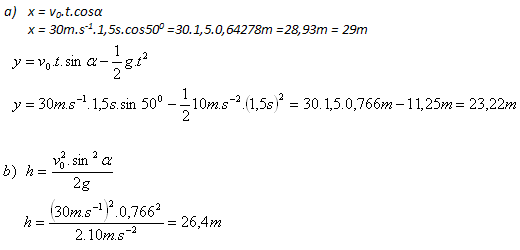
fyzika-pohyby-v-homogennom-gravitacnom-poli-9.gif 

  • a) Zur Zeit t = 1,5 s befindet sich der Körper in einer Entfernung von 29 m vom Abwurfpunkt in einer Höhe von 23,22 m.
  • b) Am Scheitelpunkt erreicht er eine maximale Höhe von 26,4 m.

10.Ein Fußball wurde von der Feldoberfläche unter einem Höhenwinkel α = 450 geschossen und landete in einer Entfernung von 40 m vom Schussort auf der Feldoberfläche. Wie groß war seine Anfangsgeschwindigkeit und welche maximale Höhe erreichte der Ball?

Lösung:

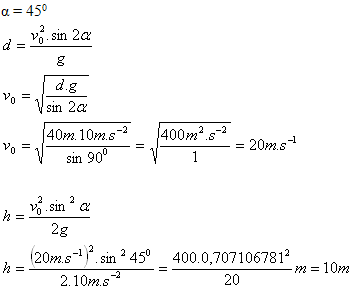
fyzika-pohyby-v-homogennom-gravitacnom-poli-10.gif 

Die Anfangsgeschwindigkeit des Balls betrug 20 m·s-1. Der Ball stieg auf eine maximale Höhe von 10 m.