Kinematik

1. Sie fahren mit dem Auto auf der Autobahn 3 Stunden lang mit einer Geschwindigkeit von 110 km·h^-1 in den Urlaub. Dann halten Sie 30 Minuten an. Anschließend fahren Sie 2 Stunden mit konstanter Geschwindigkeit von 90 km·h^-1 weiter bis zum Ziel. Bestimmen Sie die durchschnittliche Reisegeschwindigkeit.

Lösung:

Analyse:

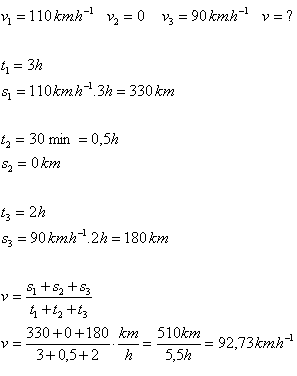
physics-kinematics-1

Die durchschnittliche Reisegeschwindigkeit betrug v = 92.73 km·h^-1.

2.Der Autobahnabschnitt ist 25 km lang. Die zulässige Höchstgeschwindigkeit beträgt 110 km·h^-1. Der Fahrer legte diesen Abschnitt in 12 Minuten zurück. Wurde die zulässige Höchstgeschwindigkeit auf der Autobahn überschritten?

Lösung:

Analyse:

s = 25 km = 2500 m; t = 12 min = 720 s.

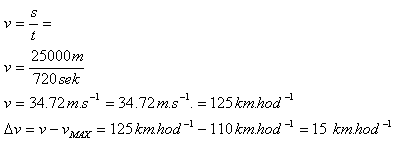
physics-kinematics-2

Der Fahrer überschritt die erlaubte Geschwindigkeit um 15 km·h^-1.

3.Ein Konvoi aus Militärfahrzeugen ist 2 km lang. Er bewegt sich mit konstanter Geschwindigkeit von 30 km·h^-1. Die Strecke von der Spitze des Konvois bis zum letzten Fahrzeug legte ein Kurier mit einer Durchschnittsgeschwindigkeit von 50 km·h^-1 zurück. Zurück fuhr er mit 60 km·h^-1. Wie viel Zeit benötigte der Kurier und welche Strecke legte er zurück?

Lösung:

Analyse:
$d = 2\,\text{km},\ v_1 = 30\,\text{km·h}^{-1},\ v_2 = 50\,\text{km·h}^{-1},\ v_3 = 60\,\text{km·h}^{-1},\ d_1 = d_2 = 2\,\text{km}$

Entgegen der Fahrtrichtung des Konvois:

d_1 = (v_2 + v_1)t_1 \Rightarrow t_1 = \frac{2\,\text{km}}{50\,\text{km·h}^{-1} + 30\,\text{km·h}^{-1}} = 0.025\,\text{h} = 1.5\,\text{min}

In derselben Richtung wie der Konvoi:

d_2 = (v_3 - v_1)t_2 \Rightarrow t_2 = \frac{2\,\text{km}}{60\,\text{km·h}^{-1} - 30\,\text{km·h}^{-1}} = \frac{1}{15}\,\text{h} = 4\,\text{min}

Gesamtzeit:
$t = t_1 + t_2 = 1.5\,\text{min} + 4\,\text{min} = 5.5\,\text{min}$

Gesamtstrecke: $s = d_1 + d_2 = (v_2 + v_1)t_1 + (v_3 - v_1)t_2 = (50 + 30)·0.025 + (60 - 30)·\frac{1}{15} = 2\,\text{km} + 2\,\text{km} = 4\,\text{$

4. Ein frei fallender Körper hat am Punkt A eine Geschwindigkeit von 3.0 m·s^-1 und am tiefer gelegenen Punkt B eine Geschwindigkeit von 7.0 m·s^-1. Bestimmen Sie die Zeit für die Strecke AB. Wie groß ist der Abstand zwischen den Punkten A und B? Mit welcher Geschwindigkeit trifft der Körper auf den Boden, wenn seine Bewegung von Punkt B bis zum Boden weitere 2 s dauert?

Lösung:

Analyse:

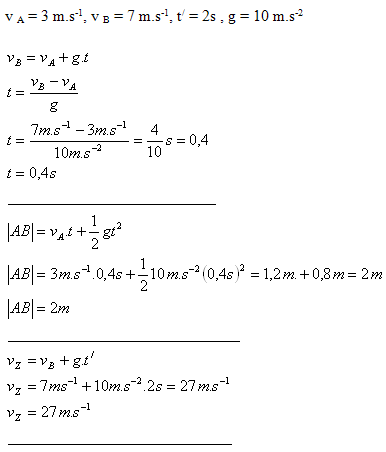
physics-kinematics-4

5. Ein Schwimmer, dessen Geschwindigkeit relativ zum Wasser 0.85 m·s^-1 beträgt, schwimmt in einem Fluss, in dem das Wasser mit 0.40 m·s^-1 fließt. Bestimmen Sie die Zeit für die Strecke von Punkt A nach B, die 90 m auseinander liegen, wenn der Schwimmer schwimmt:

a) flussabwärts
b) flussaufwärts
c) senkrecht zur Strömung (die resultierende Geschwindigkeit ist senkrecht zur Strömungsgeschwindigkeit).

Lösung:

Analyse:

v₁ = 0.85 m.s^-1, v₂ = 0.4 m.s^-1, s = 90 m

flussabwärts

flussaufwärts

senkrecht zur Strömung

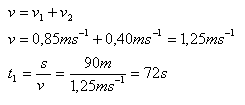
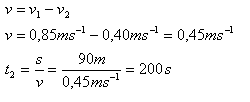
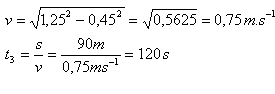
Der Schwimmer erreicht B von A aus flussabwärts in t₁ = 72 s, flussaufwärts in t₂ = 200 s und senkrecht zur Strömung in t₃ = 120 s.

6. Ein Motorboot auf einem Fluss legte flussabwärts in 14 s eine Strecke von 120 m zurück und flussaufwärts in 24 s. Bestimmen Sie die Bootsgeschwindigkeit v₁ relativ zum Wasser und die Geschwindigkeit der Flussströmung v₂.

Lösung:

Analyse:

v₁ – Bootsgeschwindigkeit relativ zum Wasser, v₂ – Geschwindigkeit der Flussströmung

t₁ = 14 s, t₂ = 24 s

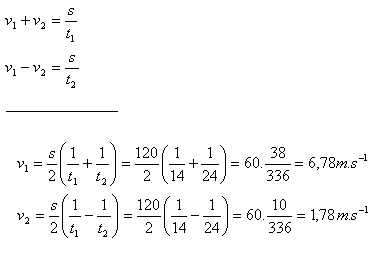
physics-kinematics-6

Die Bootsgeschwindigkeit relativ zum Wasser beträgt 6.78 m·s^-1, die Geschwindigkeit der Flussströmung 1.78 m·s^-1.

7.Ein Autofahrer legte das erste Drittel der Strecke mit konstanter Geschwindigkeit v₁ zurück und die übrigen zwei Drittel mit v₂ = 72 km·h^-1. Die Durchschnittsgeschwindigkeit v betrug 36 km·h^-1. Berechnen Sie v₁!

Lösung:

Analyse:

v₁ = ?, v₂ = 72 km·h^-1 = 20 m·s^-1, v = 36 km·h^-1 = 10 m·s^-1

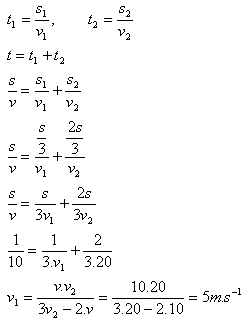
physics-kinematics-7

Das erste Drittel der Strecke wurde mit v₁ = 5 m·s^-1 zurückgelegt.

8.Ein Auto, das mit 90 km·h^-1 fuhr, sah 60 m voraus einen stehenden Lkw. Der Fahrer bremste und erreichte eine Verzögerung von a = 5 m·s^-2. Wie groß war der Bremsweg des Autos? Prallte es gegen das Hindernis?

Lösung:

Analyse:

v = 90 km·h^-1 = 25 m·s^-1, a = 5 m·s-²

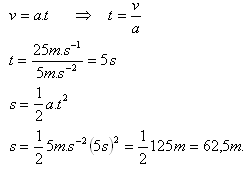
physics-kinematics-8

Der Bremsweg des Autos betrug s = 62.5 m. Das Auto stieß gegen das Hindernis.

9.Eine Rakete erreicht die zweite kosmische Geschwindigkeit von 11 km·s^-1, nachdem sie eine Strecke von 200 km zurückgelegt hat. Wie lange dauert es, dies zu erreichen? Wie groß ist ihre Beschleunigung?

Lösung:

Analyse:

v = 11 km·s^-1 = 11,000 m·s^-1, s = 200 km = 200,000 m.

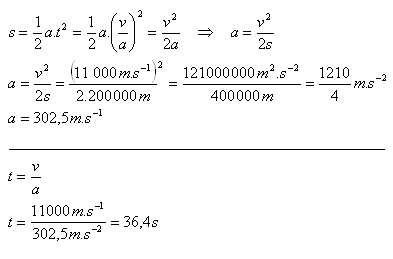
physics-kinematics-9

Die Rakete erreicht die zweite kosmische Geschwindigkeit in 36.4 s. Ihre Beschleunigung beträgt 302.5 m·s^-2.

10. Ein Wagen auf den Schienen eines Demonstrationsaufbaus bewegt sich mit konstanter Beschleunigung a = 0.08 m·s^-2 (v₀ = 0, s₀ = 0)

Berechnen Sie die Strecken, die der Wagen zu den Zeiten t = 1 s, 2 s, 3 s, 4 s, 5 s zurücklegt.
Bestimmen Sie die in jeder aufeinanderfolgenden Sekunde zurückgelegten Strecken. In welchem Verhältnis stehen diese Strecken?

Lösung:

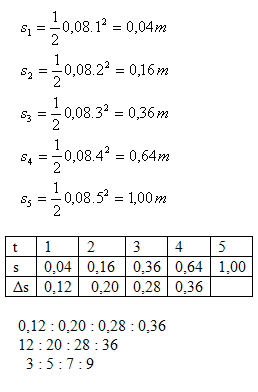
physics-kinematics-10

11.Der Lokführer eines Schnellzugs, der sich mit v₁ = 108 km·h^-1 bewegte, sah 180 m voraus einen Güterzug, der in dieselbe Richtung mit v₂ = 32.4 km·h^-1 fuhr. Der Lokführer begann zu bremsen, und der Zug verzögerte mit a = 1.2 m·s^-2. Bestimmen Sie, ob die Züge zusammenstoßen.

Lösung:

Analyse:

s₀ = 180 m, v₁ = 108 km·h^-1 = 30 m·s^-1, v₂ = 32.4 km·h^-1 = 9 m·s^-1, a = 1.2 m·s^-2

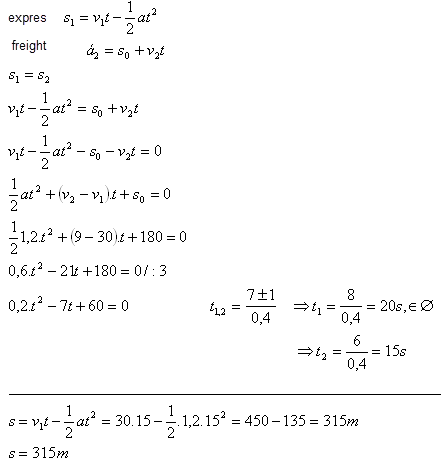
kinematics-11-r

Die Züge kollidieren 15 s nach Beginn des Bremsens in einer Entfernung von 315 m.

12.Der Sekundenzeiger einer Uhr ist um ein Drittel länger als der Minutenzeiger. In welchem Verhältnis stehen die Geschwindigkeiten ihrer Spitzen?

Lösung:

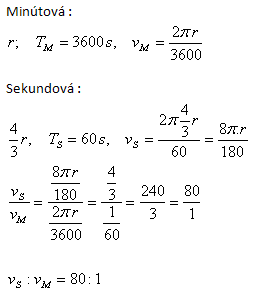
physics-kinematics-12

13.Die Erde bewegt sich in näherungsweise gleichförmiger Kreisbewegung in 365.25 Tagen um die Sonne. Wie groß ist die Geschwindigkeit der Erde, wenn der Abstand Erde–Sonne etwa 150 Millionen Kilometer beträgt?

Lösung:

T = 365.25 Tage = 31,557,600 s = 3.16·10⁷ s, r = 150,000,000 km = 1.5·10¹¹ m.

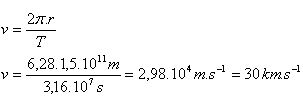
physics-kinematics-13

Die Erde bewegt sich mit einer Tangentialgeschwindigkeit von 30 km·s^-1 um die Sonne.

14.Die Geschwindigkeit der gleichförmigen Kreisbewegung eines Satelliten um die Erde beträgt 7.46 km·s^-1. Der Satellit bewegt sich in einer Höhe von 800 km über der Erdoberfläche. (R = 6378 km) Bestimmen Sie die Umlaufzeit T des Satelliten um die Erde.

Lösung:

R = 6378 km = 63.78·10⁵ m, h = 800 km = 8·10⁵ m, v = 7.46·10³ m·s^-1

r = R + h = 63.78·10⁵ m + 8·10⁵ m = 71.78·10⁵ m

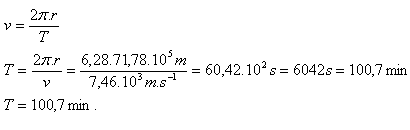
physics-kinematics-14

15.Welche Mindestgeschwindigkeit muss ein Motorradfahrer haben, um sich in alle Richtungen auf der Innenfläche einer Hohlkugel mit Radius R = 6 m bewegen zu können? Der Schwerpunkt von Motorrad und Fahrer ist 0.9 m von der Oberfläche entfernt.

Lösung:

r = R – 0.9 = 6 m – 0.9 m = 5.1 m

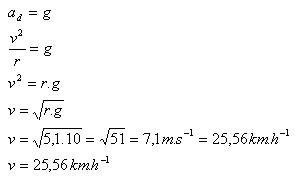
physics-kinematics-15

Die Mindestgeschwindigkeit des Motorradfahrers muss 25.56 km·h^-1 betragen.

16. Ein Karussellsitz ist in einer Entfernung von 240 cm vom Rotationszentrum befestigt und macht 18 Umdrehungen pro Minute. Bestimmen Sie seine Tangentialgeschwindigkeit und Zentripetalbeschleunigung.

Lösung:

Analyse:

r = 240 cm = 2.4 m, f = 18/60 s^-1 = 0.3 s^-1,

v = 2π·r·f

v = 6.28·2.4 m·0.3 s^-1 = 4.52 m·s^-1

v = 4.52 m·s^-1

a _c = 4π²·f²·r

a _c = 4·9.8596·0.3²·2.4 m·s^-2 = 8.52 m·s^-2

a _c = 8.52 m·s^-2

Der Karussellsitz hat eine Tangentialgeschwindigkeit von 4.52 m·s^-1

und eine Zentripetalbeschleunigung von 8.52 m·s^-2.

Physik

Kinematik

Adblock detected