Stabilität der Körper
1. Was verstehen wir unter der Stabilität von Körpern?
Lösung:
Ein starrer Körper kann sich in drei Gleichgewichtslagen befinden.
- a.) Stabile Lage – nach einer Auslenkung kehrt der Körper in seine ursprüngliche Lage zurück
- b.) Neutrale Lage – der Körper bleibt in der ausgelenkten Lage
- c.) Instabile Lage – der Körper kehrt nicht in seine ursprüngliche Lage zurück
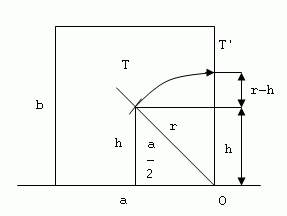Die Stabilität eines abgestützten Körpers wird durch die Arbeit bestimmt, die nötig ist, um ihn aus der stabilen in die instabile Lage zu kippen.
W = m.g.(r – h)
m – Masse des Körpers
h – Abstand des Schwerpunkts von der Auflagefläche in aufrechter Stellung
r – Abstand des Schwerpunkts von der Kante, um die der Körper gekippt wird
r – h – Anhebung des Schwerpunkts während des Kippens
Die Stabilität eines Körpers ist hoch, wenn er eine große Masse hat und sein Schwerpunkt möglichst tief liegt.
2.Die Abmessungen eines Ziegels sind a = 0.3 m, b = 0.15 m, c = 0.06 m, seine Masse beträgt 5 kg. Berechne die Arbeit, die erforderlich ist, um den Ziegel um die Kante b von der stabilen in die instabile Lage zu kippen.
Lösung:
Analyse:
a = 0.3 m, b = 0.15 m, c = 0.06 m, m = 5 kg,
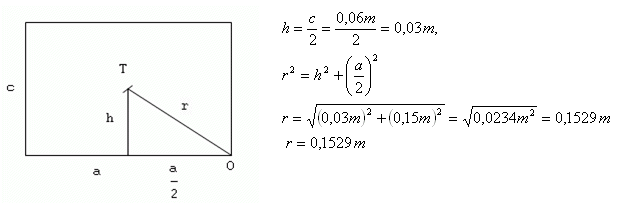
W = m.g.(r – h)
W = 5kg·10m·s-2·(0.1529m – 0.03m)
W = 50 kg·m·s-2·0.1229m = 6.145 J
W = 6.145 J
Die zum Kippen des Ziegels erforderliche Arbeit beträgt W = 6.145 J.
3.Welche Arbeit ist erforderlich, um einen Granitblock (ρ = 2800 kg·m-3) in Form eines Würfels mit der Masse 1000 kg über eine Kante von einer Fläche auf die andere zu kippen?
Lösung:
Analyse:
m = 1000 kg, ρ = 2800 kg·m-3,
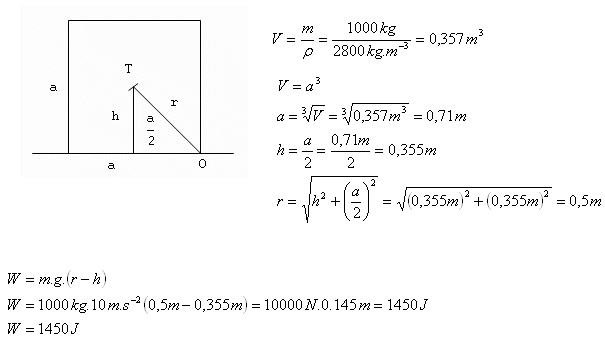
Zum Kippen des Granitblocks ist eine Arbeit von W = 1450 J erforderlich.
4.Ein schwerer Ziegelblock in Form eines Quaders mit der Höhe 2 m und der Breite 1.5 m hat eine Masse von 2500 kg. Vergleiche die Arbeit, die erforderlich ist, um den Block um die dritte Kante gemäß den Abbildungen zu kippen.
Lösung:
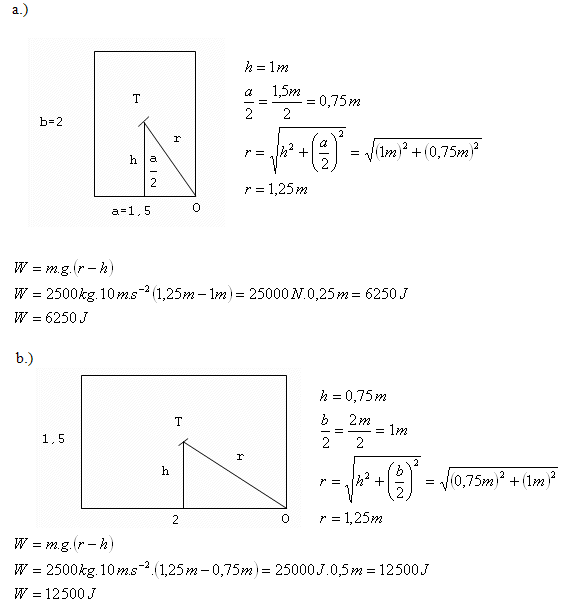
Die Arbeit ist im zweiten Fall doppelt so groß wie im ersten Fall.
5.Ein quadratisches Granitprisma (ρ = 2500 kg·m-3) hat eine Grundkante von 60 cm und eine Höhe von 80 cm. Welche Arbeit muss geleistet werden, um das Prisma aus einer stabilen Gleichgewichtslage in eine instabile zu kippen? Das Prisma steht auf einer quadratischen Grundfläche.
Lösung:
Analyse:
ρ = 2500 kg·m-3, a = 60 cm = 0.6 m, b = 80 cm = 0.8 m, W = ?
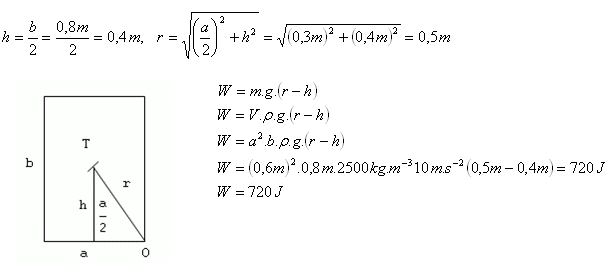
Zum Kippen des Prismas ist eine Arbeit von W = 720 J erforderlich.