Stabilita těles
1. Co rozumíme pod stabilitou těles?
Řešení:
Tuhé těleso může být ve třech rovnovážných polohách.
- a.) Poloha stálá (stabilní) - těleso po vychýlení se vrátí do původní polohy
- b.) Poloha volná (indiferentní)-těleso zůstane ve vychýlené poloze
- c.) Poloha vratká (labilní) - těleso se nevrátí do původní polohy
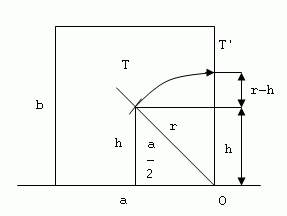 Stabilita podepřeného tělesa se určuje velikostí práce, kterou je třeba provést, abychom těleso převrátili z polohy stabilní do polohy vratké.
Stabilita podepřeného tělesa se určuje velikostí práce, kterou je třeba provést, abychom těleso převrátili z polohy stabilní do polohy vratké.
W = m.g.(r – h)
m - hmotnost tělesa
h - vzdálenost těžiště od podstavy v nepřeklopené
poloze
r - vzdálenost těžiště od hrany kolem níž těleso překlápět
r - h - zvýšení těžiště při překlápění
Stabilita tělesa je velká, pokud těleso má velkou hmotnost a jeho těžiště je co nejnižší.
2.Rozměry cihly jsou a = 0,3 m, b = 0,15 m, c = 0,06 ma její hmotnost je 5 kg. Vypočítejte práci, kterou je třeba vynaložit na převrácení cihly kolem hrany b ze stálé do vratké polohy.
Řešení:
Rozbor:
a = 0,3 m, b = 0,15 m, c = 0,06 m, m = 5 kg,
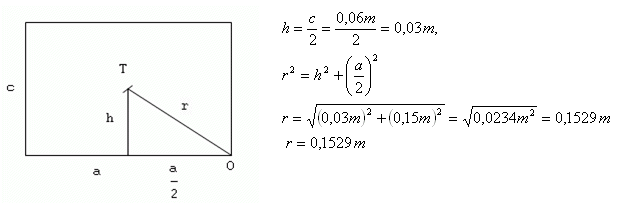
W = m.g.(r – h)
W = 5kg.10m.s-2.(0,1529m – 0,03m)
W = 50 kg.m.s-2.0,1229m = 6,145 J
W = 6,145 J
Na převrácení cihly třeba vynaložit práci W = 6,145 J.
3.Jakou práci je třeba vykonat při převrácení žulového bloku (ρ = 2800 kg.m-3) tvaru krychle o hmotnosti 1000 kg, přes hranu, z jedné její stěny na druhou?
Řešení:
Rozbor:
m = 1000 kg, ρ = 2800 kg.m-3,
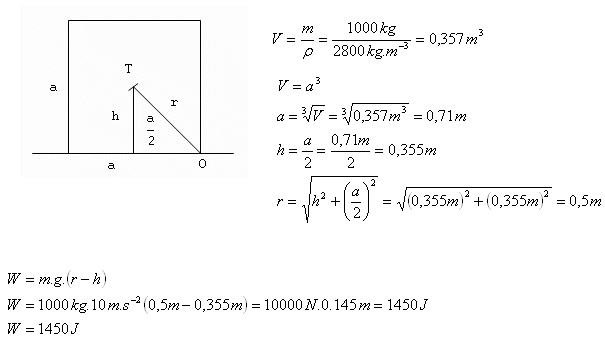
Na převrácení žulového bloku třeba vykonat práci W = 1450 J
4.Těžký cihlový blok tvaru kvádru s výškou 2m a šířkou 1,5 m má hmotnost 2500 kg. Porovnejte práce potřebné při převracení bloku kolem třetí hrany podle obrázků.
Řešení:
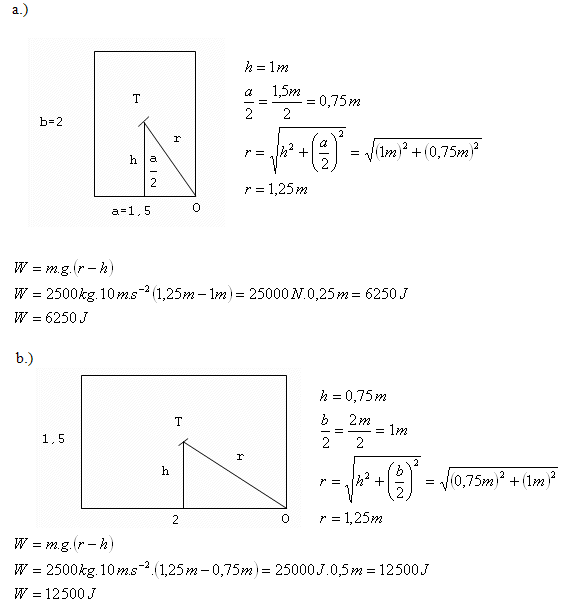
Práce v druhém případě je dvakrát větší než v prvním případě.
5.Žulový čtyřboký pravidelný hranol (ρ = 2500 kg.m-3) má podstavovú hranu 60 cm a výšku 80 cm. Jakou práci musíme vykonat, abychom hranol překlopily z rovnovážné stabilní polohy do vratké polohy. Hranol je postaven na čtvercové podstavě.
Řešení:
Rozbor:
ρ = 2500 kg.m-3, a = 60 cm = 0,6 m, b = 80 cm = 0,8 m, W = ?
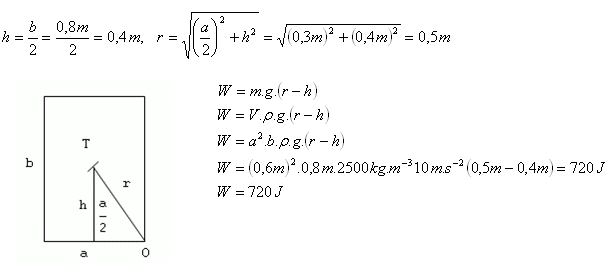
Na překlopení hranolu potřebujeme práci W = 720 J.