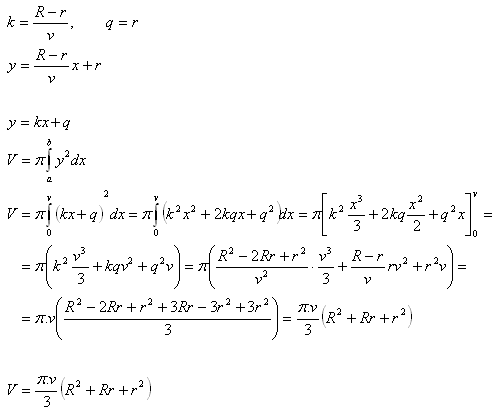Kubatura
1.Vysvětlete pojem kubatura!
Řešení:
Kubatura je výpočet objemu rotačních těles. Počítáme objem tělesa, které vznikne rotací rovinného útvaru (obdélníku, trojúhelníku, lichoběžníku, kruhu, atd..) Kolem osy x. Rovinný útvar je ohraničen osou x, přímkami x1 = a, x2 = b a čarou y = f (x).
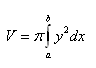
2.Odvoďte vzorec pro objem rotačního válce, který má poloměr podstavy r, a výšku v.
Řešení:
Těleso vznikne rotací obdélníku kolem osy x. Obdélník je ohraničen osou x a přímkami x1=a=0, x2=b= v, y = r.
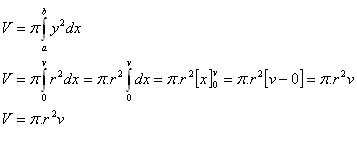
3. Odvoďte vzorec pro výpočet objemu rotačního kužele, jehož poloměr podstavy je ra výška v.
Řešení:
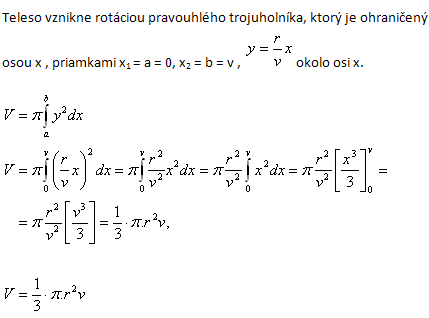
4.Odvoďte vzorec pro výpočet objemu koule o poloměru r!
Řešení:
Těleso vznikne rotací kružnice x2 + y2 = r2 kolem osi x.
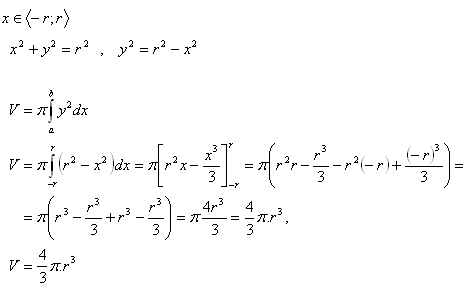
5.Odvoďte vzorec pro výpočet objemu rotačního elipsoidu s poloosami a, b.
Řešení:
Těleso vznikne rotací elipsy kolem osy x. Elipsa má rovnici:
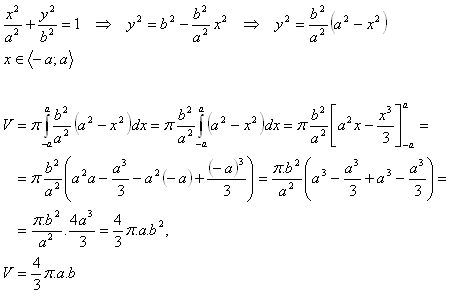
6.Odvoďte vzorec pro výpočet objemu rotačního parabolidu, který vznikne rotací paraboly y2 = 2px kolem osy x. Paraboloid má výšku v.
Řešení
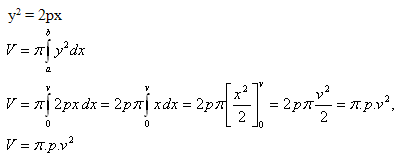
7.Vypočtěte objem tělesa, které vznikne rotací funkce y = cosx kolem osy x
Řešení:
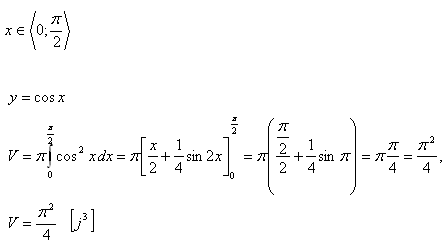
8. Odvoďte vzorec pro výpočet objemu komolého kužele. Dolní podstava má poloměr R, horní r.. Výška kužele je v.
Řešení:
Těleso vznikne rotací rovnoramenného lichoběžníku kolem osy x. Lichoběžník je ohraničen osou x, dvěma přímkami x1 = a = 0, x2 = b = v a přímkou y = kx + q, kde konstanty kaq znamenají