Povrch kapalin
1. Vysvětlete fyzikální pojmy "povrchová vrstva" a "kapilarita"
Řešení:
Hladina a kapka kapaliny, bublina se chovají tak, jako by na jejich povrchu byla pružná blanka - "povrchová vrstva". Má tloušťku asi 10-9m. Je tvořena vrstvou molekul. Hladina a kapka mají jeden povrch, bublina dva povrchy.
Povrchové napětí:

l = 2π.r S = π.r2
- Kapilární elevace = zvýšení hladiny smáčivé kapaliny v kapiláře
- Kapilární deprese = snížení hladiny nesmáčivá kapaliny v kapiláře
2.Jaká je hmotnost kapky vody (σ = 73.10-3N.m-1), která okapy z trubky s poloměrem 0,5 mm?
Řešení:
Rozbor:
R = 0,5.10-3m, g = 10 m.s-2, σ = 73.10-3N.m-1
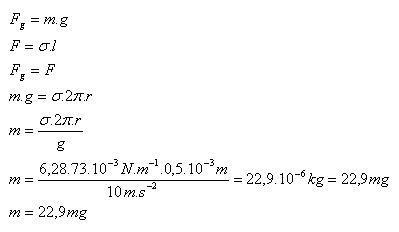
Hmotnost kapky vody je m = 22,9 mg.
3.Kapilára změřila 100 kapek lihu s hmotností 1,81 g. Stejný počet kapek vody z téže kapiláry a téže teploty má hmotnost 6,26 g. Určitě povrchové napětí lihu σ1 (líh) pokud víte, že povrchové napětí vody je σ2(H2O) = 73.10-3N.m-1.
Řešení:
Rozbor:
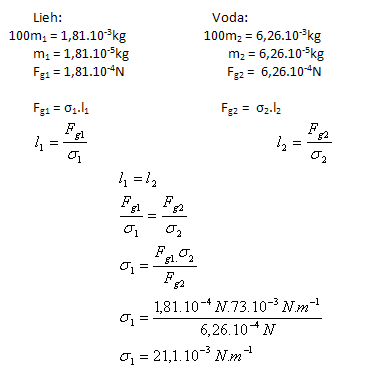
Povrchové napětí líhu je σ1 = 21,1,10-3 N.m-1
4.Voda odkapává z kapiláry o poloměru r = 0,9 mm. Kolik kapek vody je v 1 cm3 vody?
(σ = 73.10-3N.m-1, ρ = 103kg.m-3)
Pro zobrazení řešení se přihlaste.
5.Pohyblivá příčka s délkou 40mm na rámečku s mýdlovou blánou je v rovnováze, pokud je zatížena závažím o hmotnosti 320 miligramů. Jaké je povrchové napětí mýdlového roztoku ve vodě ve styku se vzduchem? Blána má dva povrchy. (Hmotnost příčky zanedbat)
Pro zobrazení řešení se přihlaste.
6. Určete práci (při izotermickém ději), kterou je třeba provést při nafouknutí mýdlové bubliny s průměrem 14 cm. Bublina má dva povrchy. σ = 40.10-3N.m-1
Pro zobrazení řešení se přihlaste.
7.Mýdlová bublina (σ = 40.10-3N.m-1) má poloměr 2cm. Jakou práci vykonáme, pokud zvětšíme její poloměr o 1cm?
Pro zobrazení řešení se přihlaste.
8. Kapilární zvýšení - elevace - lihu je v úzké kapiláře 12mm. Jaký je vnitřní průměr kapiláry?
(ρ = 800 kg.m-3, σ = 21,4 mN.m-1)
Pro zobrazení řešení se přihlaste.
9.Kapilára má vnitřní průměr 0,2 mm. Vypočítejte:
- a.) Jak vysoko vystoupí v kapiláře benzén (ρ = 870 kg.m-3, σ = 29,1.10-3N.m-1)
- b.) Jak se změní výška výstupu benzenu, pokud použijeme kapiláru s dvojnásobným poloměrem
- c.) Jak by se změnil výsledek pokusu na Měsíci. (gM = 0,167g)
10. Jaký bude rozdíl hladin ve dvou kapilárách ponořených do kapaliny (ρ = 800 kg.m-3, σ = 22.10-3N.m-1). Kapiláry mají rozdílné průměry vnitřního povrchu: d1 = 0,4mm, d2 = 1mm
Pro zobrazení řešení se přihlaste.
11.Na rámu s pohyblivou příčkou s délkou 10 cm je mýdlová bublina. Jakou práci je třeba vykonat, aby se příčka posunula o 2cm.
Pro zobrazení řešení se přihlaste.12.Rámeček s pohyblivým ramenem s hmotností 1,2 g je ve svislé poloze. Tíhová síla prodlužuje rameno a blánu v rovnováze. Jaká je délka ramene, pokud povrchové napětí blány je 60.10-3N.m-1. Jak se změní povrchová energie blány, pokud se rameno posune o 2cm.
Pro zobrazení řešení se přihlaste.13.Vodní kapku o poloměru 3mm rozprášíme na drobné kapičky o poloměru 3.10-5mm. Kolikrát se při tom zvětší povrchová energie vodních kapek?
Pro zobrazení řešení se přihlaste.14.Jaký tlak má vzduch v mýdlové bublině o poloměru 2 mm, pokud atmosférický tlak je 101325 Pa?
Pro zobrazení řešení se přihlaste.15.V kapiláře vystoupil petrolej do výšky 13mm av jiné kapiláře se stejným poloměrem poklesla rtuť o 13,9 mm. Jaké je povrchové napětí rtuti, pokud hustota rtuti je 13,6.103kg.m3. Povrchové napětí petroleje je 27.10-3N.m-1 a jeho hustota je 0,8.103kg.m-3.
Pro zobrazení řešení se přihlaste.16. V kapiláře o průměru 2 mm je voda. Jak vysoký sloupec vody zůstane v kapiláře, pokud oba její konce zůstanou otevřené.
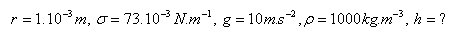
17.Z kapiláry odkapalo 100 kapek vody celkové hmotnosti 2,4 g. Hmotnost 50 kapek glycerinu z téže kapiláry je 1,1 g. Jaký je poměr povrchových napětí obou kapalin?
Pro zobrazení řešení se přihlaste.18. Jaké je povrchové napětí glycerinu? (Použijte výsledek příkladu 17)
Pro zobrazení řešení se přihlaste.19.Při spojení N vodních kapek s poloměrem 2.10–6m do jedné kapky s poloměrem 2.10–3m se uvolní 3,668 mJ energie. O kolik se voda ohřeje?
Pro zobrazení řešení se přihlaste.20.Vypočtěte povrchovou energii kapky rtuti, která má objem 1cm3.
Pro zobrazení řešení se přihlaste.