Variace
1. Definujte a charakterizujte variace a variace s opakováním.
Řešení:
Variace
Variace k-té třídy zn prvků je každá uspořádaná k-tice různých prvků vybraných z n-elementární množiny. V k-tici záleží na pořadí prvků. V k-tici se ani jeden z prvků neopakuje. Počet variací:
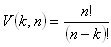
Variace s opakováním
Variace k-té třídy zn prvků s opakováním je každá uspořádaná k-tice prvků vybraných z n-elementární množiny. V k-tici se mohou prvky libovolně opakovat.
Počet variací s opakováním:
V*(k,n) = nk
2. Daná je množina M = {a,b,c,d}. Z prvků této množiny vytvořte variace 2.triedy bez opakování as opakováním. Vypočtěte jejich počet.
Řešení:
a) Variace:
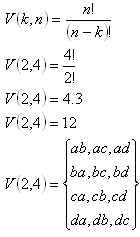
b) Variace s opakováním:
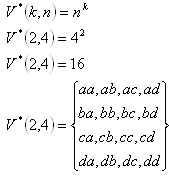
3. Do školského výboru zvolili 7 žáků. Kolika způsoby se dá z nich vybrat předseda, místopředseda, tajemník a pokladník?
Řešení:
Jsou to variace: n = 7, k = 4
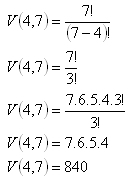
Funkcionáři výboru se dají vybrat 840 způsoby.
4. Osm studentů si slíbilo, že si z prázdninových cest vzájemně vyměňují pohlednice.
Kolik pohlednic rozeslali?
Řešení:
Jsou to variace: n = 8, k = 2
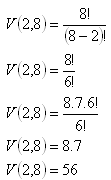
Studenti rozeslali 56 pohlednic.
5. Z kolika různých prvků můžeme vytvořit 240 variací 2.triedy?
Řešení:
Jsou to variace: n = x, k = 2
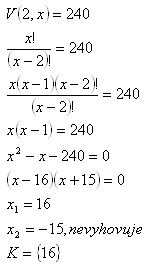
Potřebujeme 16 prvků.
6. Pokud se počet prvků zvětší o 2, zvětší se počet variací 3. třídy o 384. Kolik je prvků?
Řešení:
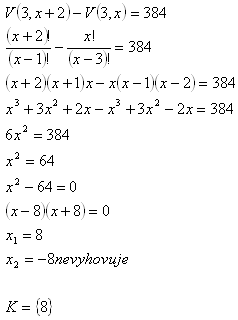
Prvků je 8.
7. V kapse je 6 různých lístků označených čísly 1 až 6. Kolika různými způsoby můžeme postupně, s přihlédnutím k pořadí vybrat tři z nich, pokud vybrané lístky do kapsy
- a) nevracejí.
- b) vracejí.
Řešení:
a) nevracejí
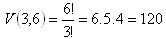
b) vracejí
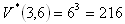
Kartičky môžeme z vrecka vybrať 120 alebo 216 spôsobmi.
8.Počet variací bez opakování 3.třídy z x prvků je o 225 menší než počet variací 3. triedy s opakováním ze stejných prvků. Kolik je prvků?
Řešení:
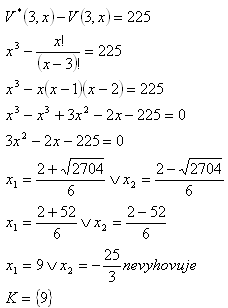
9.Počet tříčlenných variací bez opakování je 10 násobkem dvoučlenných variací bez opakování téže množiny prvků. Kolik prvků má tato množina?
Řešení:
Počet prvků množiny: x
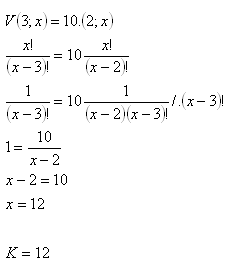
Počet prvků množiny je x = 12
10.Hoďme třemi kostkami - bílou, modrou, žlutou.
- a.) Kolik různých výsledků můžeme dostat?
- b.) Kolik různých součtů může padnout?
- c.) Kolika způsoby může padnout součet 13
Řešení:
a.) V/(k;n) = nk, V/(3;6) = 63 = 216
b.) Může padnout součet : 3;4;5;6;7;8;9;10;11;12;13;14;15;16; 17;18, n = 16 součtů
c.) Součet 13: