Kinematika
1. Na dovolenou jedete autem po dálnici 3 hodiny rychlostí 110 km.h-1.Potom na 30 minut zastavíte. Pokračujete dvouhodinovou jízdou stálou rychlostí 90 km.h-1 až do cíle. Určitě průměrnou rychlost cestování.
Řešení:
Rozbor:
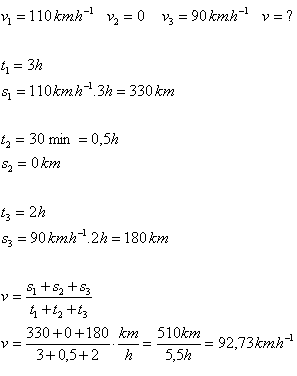
Průměrná rychlost cestování byla v = 92,73 km.hod-1.
2.Dálniční úsek má délku 25 km. Největší povolená rychlost je 110 km.hod-1. Řidič tento úsek prošel za 12 minut. Překročil největší povolenou rychlost na dálnici?
Řešení:
Rozbor:
s=25 km = 25000 m; t=12 min = 720 sek.
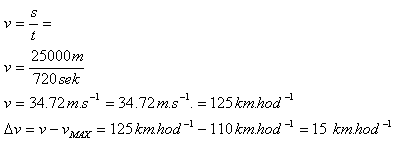
Řidič překročil dovolenou rychlost o 15 km.hod-1
3.Kolona vojenských vozidel má délku 2 km. Pohybuje se stálou rychlostí 30 km.hod-1. Vzdálenost od čela kolony ke poslednímu vozidlu prošla spojka průměrnou rychlostí 50 km.h-1. Zpět rychlostí 60 km.h-1. Jaký čas na to spojka na to potřebovala jakou dráhu při tom prošla?
Řešení:
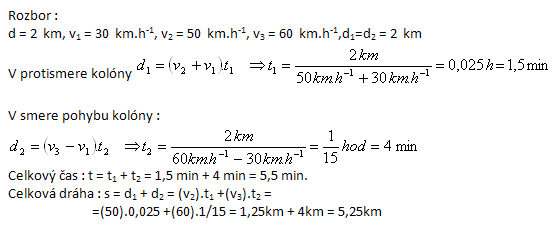
4. Volně padající těleso má v bodě A rychlost 3,0 ms-1, v níže položeném bodě B rychlost 7,0 ms-1. Zjistěte za jaký čas ujede vzdálenost AB. Jaká je vzdálenost bodů A a B? Jakou rychlostí těleso dopadne, pokud jeho pohyb z bodu B na zem trvá ještě 2 s.
Řešení:
Rozbor:
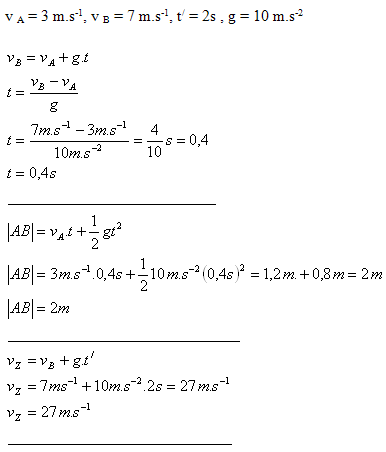
5.Plavec, jehož rychlost vzhledem na vodu je 0,85 ms-1 plave v řece, v níž voda teče rychlostí 0,40 ms-1. Určete čas, za který dopluje z místa A do B, vzdáleného 90 m, pokud plave:
- a) po proudu
- b) proti proudu
- c) kolmo na proud (Výsledná rychlost je kolmá na rychlost proudu).
Řešení:
Rozbor:
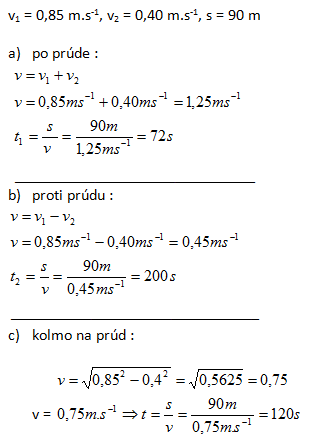
Plavec z A do B dopluje po proudu za t1 = 72s, proti proudu za t2 = 200s a kolmo na proud za t3 = 120s.
6. Motorová loď plovoucí po řece prošla vzdálenost 120 m při plavbě po proudu za 14s, při plavbě proti proudu za 24s. Určitě rychlost loďky v1 vzhledem na vodu s rychlost proudu řeky v2.
Řešení:
Rozbor:
v1 – rychlost loďky vzhledem na vodu , v2 - rychlost proudu řeky
t1 = 14s, t2 = 24s
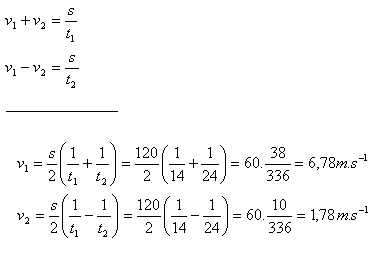
Rychlost loďky vzhledem na vodu je 6,78 m.s-1, - rychlost proudu řeky je 1,78m.s-1
7.Automobilista prošel první třetinu dráhy s stálou rychlostí v1, další dvě třetiny rychlostí v2 = 72 km.h-1. Průměrná rychlost v byla 36 km.h-1. Vypočtěte v1!
Řešení:
Rozbor:
v1 = ? , v2 = 72 km.h-1 = 20 ms-1, v = 36 km.h-1 = 10 m.s-1
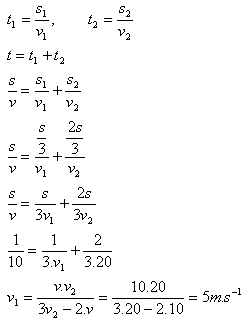
První třetinu dráhy prošel rychlostí v1 = 5 m.s-1
8.Řidič osobního auta jedoucího rychlostí 90 km.h-1 spatřil ve vzdálenosti 60 m před sebou stojící nákladní auto. Zatlačil brzdy a dosáhl zpomalení a = 5 ms-2. Jaká byla brzdná dráha osobního auta? Narazilo do překážky?
Řešení
Rozbor :
v = 90 km.h-1= 25 m.s-1, a = 5 m.s-2
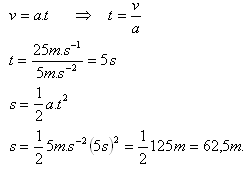
Brzdná dráha osobního auta byla s = 62,5 m. Auto narazilo do překážky.
9.Raketa dosáhne druhou kosmickou rychlost 11 km.s-1po ujetí dráhy 200 km. Za jaký čas to dosáhne? Jaké je její zrychlení?
Řešení:
Rozbor :
v = 11 km.s-1= 11 000 m.s-1, s = 200 km = 200 000 m.
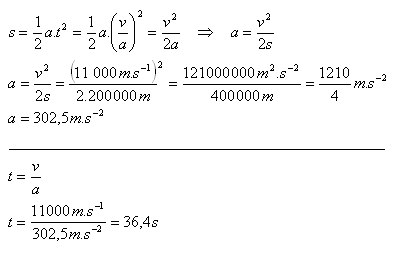
Raketa dosáhne druhou kosmickou rychlost za 36.4s. Její zrychlení je 302,5 m.s-2.
10.Vozík na kolejích vozíčkovej demonstrační soupravy se pohybuje se stálým zrychlením
a = 0,08 m.s-2 ( v0 = 0 , s0 = 0 )
- Vypočítejte dráhy, které prošel vozík v čase t = 1s, 2s, 3s, 4s, 5s.
- Zjistěte, jaké dráhy projde vozík v jednotlivých po sobě jdoucích sekundách. V jakém poměru jsou tyto dráhy?
Řešení:
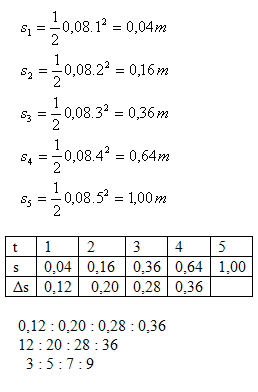
11.Strojvedoucí rychlíku, který se pohyboval rychlostí v1 = 108 km.h-1 spatřil ve vzdálenosti 180 m před sebou nákladní vlak pohybující se stejným směrem rychlostí v2 = 32,4 km.h-1. Strojvedoucí začal brzdit a vlak zpomalil se zpomalením a = 1,2 ms-2. Zjistěte, zda se vlaky srazí.
Řešení:
Rozbor :
s0 = 180 m, v1 = 108 km.h-1 = 30 m.s-1, v2 = 32,4 km.h-1 = 9 m.s-1, a = 1,2m.s-1
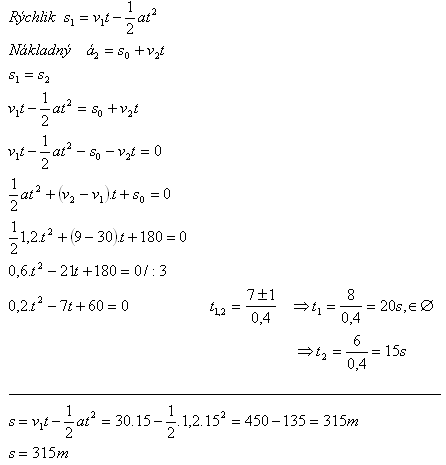
Vlaky se srazí v čase 15 s od zahájení brzdění ve vzdálenosti 315 m.
12.Sekundová ručička hodinek je o třetinu delší než minutová. V jakém poměru jsou rychlosti jejich koncových bodů?
Řešení:
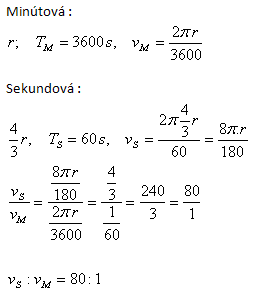
13.Země obíhá kolem Slunce přibližně rovnoměrným pohybem po kružnici za 365,25 dne. Jaká je rychlost Země, pokud vzdálenost Země - Slunce je přibližně 150 milionů kilometrů.
Řešení:
T = 365,25 dňa = 31557600 s =3,16.107s, r =150 000 000 km = 1,5.1011m.
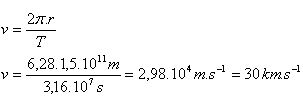
Země obíhá kolem Slunce obvodovou rychlostí 30 km.s-1
14.Rychlost rovnoměrného pohybu družice po kružnici kolem Země je 7,46 km.s-1. Družice se pohybuje ve výšce 800 km nad povrchem Země. (R = 6378 km) Určitě oběžnou dobu T družice kolem Země.
Řešení:
R = 6378 km = 63,78.105m, h = 800 km = 8.105m, v = 7,46.103 m.s-1
r = R + h = 63,78.105m + 8.105m = 71,78.105m
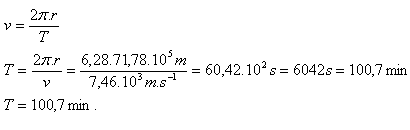
15.Jakou nejmenší rychlost musí mít motocyklista, má-li jezdit na vnitřním povrchu duté koule o poloměru
R = 6m všemi směry? Těžiště motocyklu a jezdce je 0,9 m od povrchu.
Řešení:
r = R – 0,9 = 6m - 0,9m = 5,1 m
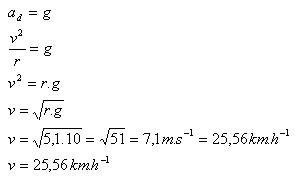
Nejmenší rychlost motocyklistu musí být 25,56 km.h-1
16. Sedačka kolotoče je upevněna ve vzdálenosti 240 cm od středu otáčení a vykonává 18 otáček za minutu. Určitě jí obvodovou rychlost a dostředivé zrychlení.
Řešení:
Rozbor :
r = 240 cm = 2,4 m, f = 18/60 s-1 = 0,3 s-1,
a)
v = 2π.r.f
v = 6,28.2,4m.0,3 s-1= 4,52 m.s-1
v = 4,52 m.s-1
b)
a d = 4π2.f2.r
a d = 4.9,8596.0,32.2,4 m.s-2= 8,52 m.s-2
a d = 8,52 m.s-2
Sedačka kolotoče má obvodovou rychlost 4,52 ms-1 a dostředivé zrychlení 8,52 ms-2.