Elektrický proud v kovech
1.Charakterizujte důležité vlastnosti stejnosměrného elektrického proudu!
Řešení:

2.Při rozjíždění elektrické soupravy ozubnicové dráhy se odebírá z vedení proud 500A. Určitě celkový elektrický náboj, který přenesou volné elektrony za 1 minutu. Kolik elektronů přešlo vodičem? e = 1,602.10-19C.
Řešení:
Rozbor:
I = 500A, t = 60s, e = 1,602.10-19C Q = ?, n = ?
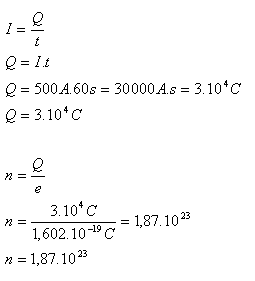
Celkový elektrický náboj přenesen elektrony je Q = 3.104C. Řidičům prošlo 1,87.1023 elektronů.
3.Telegrafní kabel z mědi (ρ = 0,017.10-6Ώ. M) mezi Snina a Humenného měl průřez 8mm2 a rezistenci 46,75 Ώ. Jakou měl délku?
Řešení:
Rozbor:
S = 8.10-6m2, R = 46,75 Ώ, ρ = 0,017.10-6Ώ.m, l = ?
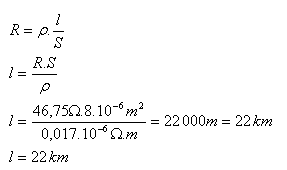
Kabel měl délku 22 km.
4.Nikelínový drát (ρ1 = 0,4.10-6Ώm) má délku l1 = 1,25m. Jakou délku by měl konštantánový drát (ρ2 = 0,5.10-6Ώm) se stejným průřezem a stejným ohmický odpor?
Řešení:
Rozbor:
l1 = 1,25m, ρ1 = 0,4.10-6Ώm, ρ2 = 0,5.10-6Ώm, l2 = ?
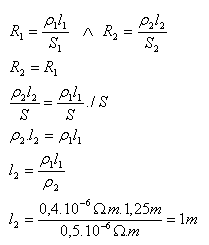
Délka konštantánového drátu by byla l2 = 1m.
5.Platinový odporový teploměr (α = 3,9.10-3K-1) má při teplotě 200C odpor 500Ώ. Odpor teploměru v rozpálené peci je 2500Ώ. Jaká je teplota pece?
Řešení:
Rozbor:
R20 = 500Ώ, Rt = 2500Ώ, α = 3,9.10-3K-1, t1 = 200C, Δt = ?, t2 = ?
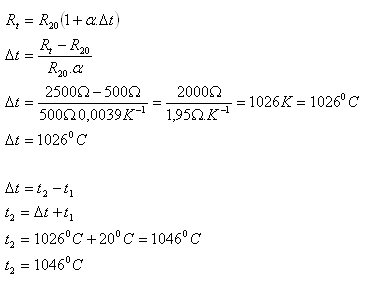
Teplota rozpálené pece je 10460C.
6.Drát z mědi (ρ1 = 0,02.10-6Ώm) s průměrem d1 = 4mm je třeba nahradit hliníkovým drátem (ρ2 = 0,03.10-6Ώm) stejné délky. Jaký hrubý musí být hliníkový drát, aby se odpor nezměnil?
Řešení:
Rozbor:
d1 = 4.10-3m, ρ1 = 0,02.10-6Ώm, ρ2 = 0,03.10-6Ώm, d2 = ?
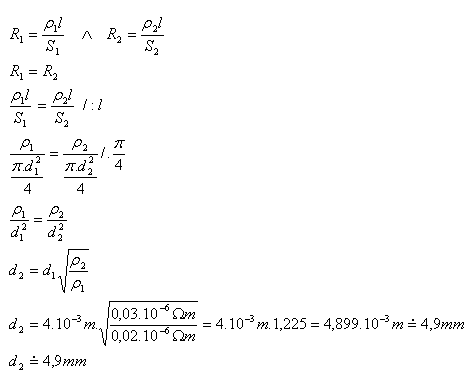
Tloušťka hliníkového drátu musí být asi 4,9 mm.
7.Dva rezistory R1, R2 při sériovém zapojení mají výsledný odpor 5 Ώ, při paralelním 1,2 Ώ. Jaké odpory mají jednotlivé rezistory?
Řešení:
Rozbor:
R1 = x, R2 = y
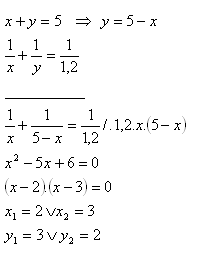
Odpory rezistorů jsou R1 = 2 Ώ a R2 = 3 Ώ, nebo R1 = 3 Ώ a R2 = 2 Ώ
8.Rezistor s odporem R = 3,8 Ώ je zapojen na elektromotorické napětí Ue = 12V. Obvodem prochází proud I = 3A. Určitě vnitřní odpor, svorkové napětí a maximální proud.
Řešení:
Rozbor:
R = 3,8Ώ, Ue = 12V, I = 3A, Ri = ?. U = ?, Imax=?
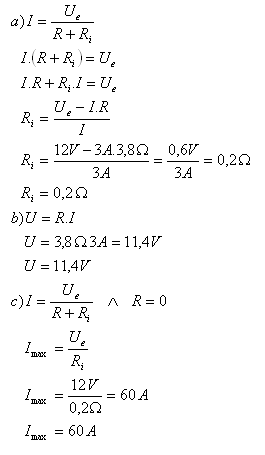
Vnitřní odpor je Ri = 0,2 Ώ, svorkové napětí U =11,4V a maximální (zkratový) proud Imax = 60A.
9.Ke zdroji elektromotorického napětí 15 V s vnitřním odporem 5 Ώ je připojen rezistor s odporem 10 Ώ. Ke svorkám zdroje napětí je paralelně připojen kondenzátor s kapacitou 1μ F. Určitě náboj na kondenzátoru!
Řešení:
Rozbor:
R = 10 Ώ, Ri = 5 Ώ, Ue = 15 V, C = 10-6F, Q = ?
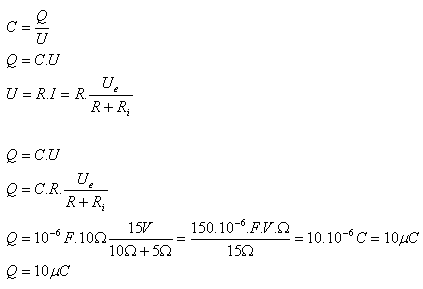
Náboj kondenzátoru je Q = 10 μC.
10.Zopakujte si znalosti krátkým testem!
1.) Dohodnutý směr elektrického proudu v kovech je směr pohybu
a.) částice s kladným elektrickým nábojem
b.) částice se záporným elektrickým nábojem
c.) částice bez náboje
A.) a,b,c B.) a C.) b, c

Řešení:
1B, 2C, 3B, 4A, 5C, 6B, 7C.
11. Přímým vodičem délky da elektrickým odporem R prochází konstantní proud I. Vypočítejte velikost intenzity elektrického pole v tomto vodiči pokud platí:
Řešení:
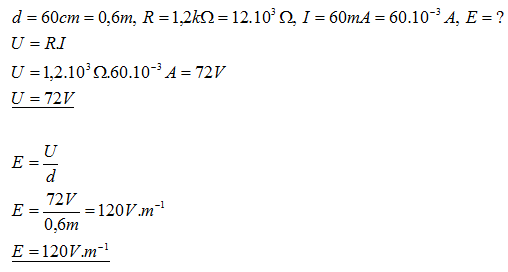
Intenzita elektrického pole ve vodiči je 120 V.m–1.
12. Vláknem wolframové žárovky s teplotou 280C prochází při napětí 10 V proud 300 mA. Určetě teplotu vlákna svítící žárovky, pokud vláknem prochází proud 0,5 A a napětí na koncích vlákna je 220 V.
Řešení:
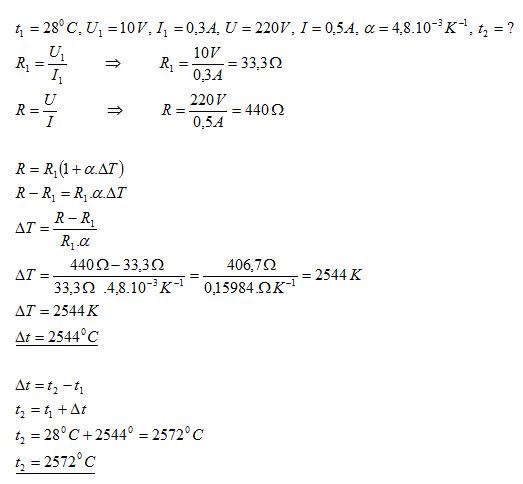
Vlákno svítící žárovky má teplotu 25440C.
13. Vodičem s odporem 15 ohmů prošel za 2 minuty elektrický náboj 30C.
- a.) Kolik elektronů vodičem prošlo
- b.) Jak velký proud prošel vodičem
- c.) Jaké bylo napětí na konci vodiče
Řešení:
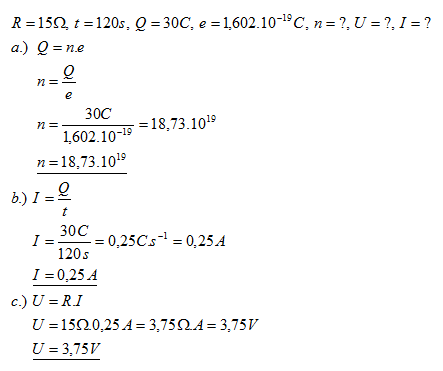
- Vodičem prošlo 18,73.1019 elektonů.
- Vodičem prošel proud 0,25 A.
- Na konci vodiče bylo napětí 3,75 V.
14. Vzdálenost elektrárny od města, které elektrárna zásobuje elektrickou energií je 900 km. Za jaký čas od zapnutí proudu v elektrárně začnou ve městě pracovat elektrické spotřebiče. Rychlost, kterou se ve vodiči šíří elektrické pole je v = c.
Řešení:
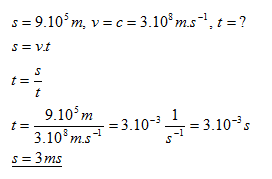
Elektrické spotřebiče ve městě začnou pracovat za 3 milisekundy.
15.Měděný drát o průměru d1 = 2mm máme nahradit hliníkovým drátem, který má stejnou délku i stejný odpor. Jaký musí být poloměr hliníkového drátu.
Řešení:
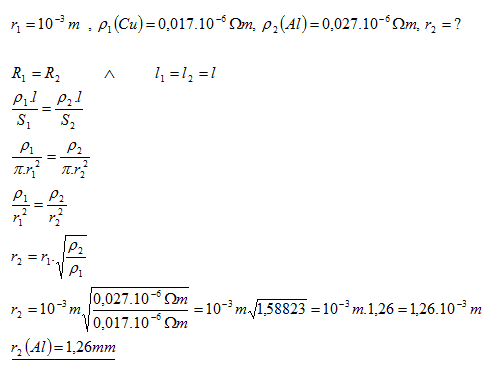
Poloměr hliníkového drátu musí být 1,26 mm.
16.Určete hmotnost mědi potřebné na zhotovení elektrického vedení se dvěma vodiči, každý délky 5km, pokud odpor vedení nemá překročit 5 ohmů.
Řešení:
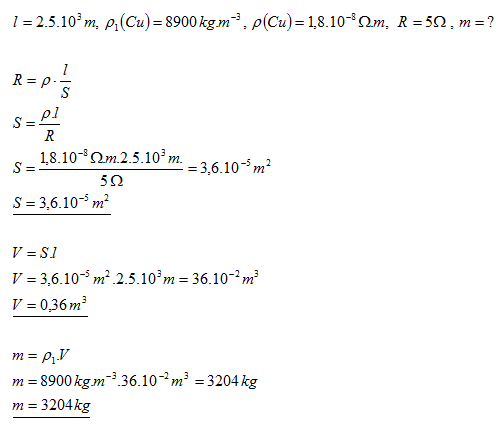
Na zhotovení elektrického vedení je potřeba 3204 kg mědi.
17.Jak velké napětí bude mezi dvěma body hliníkového drátu o průměru 0.2 mm, pokud jsou tyto body od sebe vzdáleny 10 cm. Vodičem protéká proud 1 A.
Řešení:
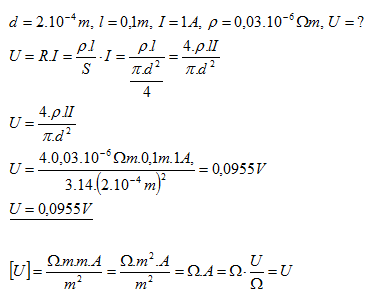
Mezi dvěma body hliníkového drátu bude napětí 0,0955 V.
18. Při zvýšení teploty termistoru se jeho odpor zmenšil o 30%. O kolik procent se při tom zvětšil proud procházející termistorem?
Řešení:
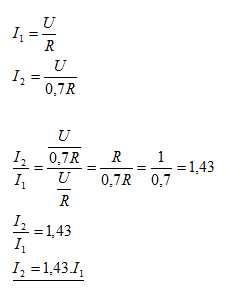
Proud se zvětšil o 43%.
19.V homogenním kovovém vodiči dlouhém l = 5m a průměrem d = 1,2 mm, jehož konce jsou připojeny k elektrickému napětí U = 4,5 V je stálý proud I = 5A. určitě:
- a.) počet elektronů, který projde vodičem za 1 ms
- b.) odpor a měrný odpor vodiče
Řešení:
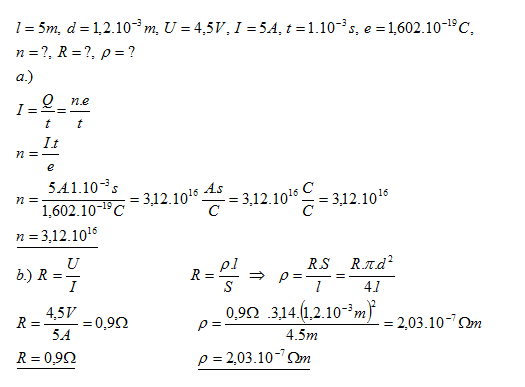
- Vodičem za 1 milisekundu projde 3,12.1016 elektronů. Odpor vodiče je 0,9 Ώ.
- Měrný odpor vodiče je 2,03.10-7 Ώm.
20. Určete hmotnost mědi potřebné na zhotovení elektrické dvojlinky délky l = 5 km, pokud odpor vodiče je R = 5 Ώ. Hustota mědi je ρ/(Cu) = 8,9.103.kg.m-3 a měrný elektrický odpor je ρ(Cu) = 0,017.10–6Ώm. Kolik stojí materiál na toto zařízení, pokud 1 kg mědi stojí 40 €.
Řešení:
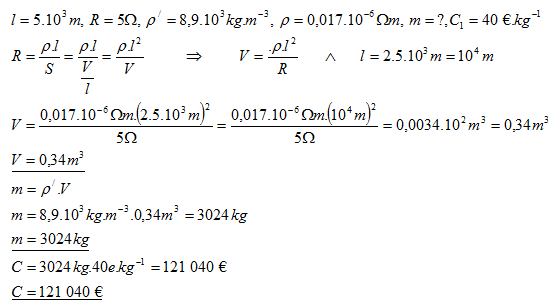
Cena 3024 kg mědi je 121 040 €.
21.Pokud na akumulátor připojíme vodič s R1 = 3,95 Ώbude jím procházet proud I1 = 3A. při odporu R2 = 2,95 Ώ zase proud I2 = 4 A, Určete vnitřní odpor akumulátoru.
Řešení:
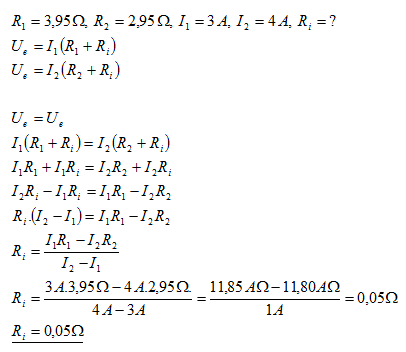
Vnitřní odpor akumulátoru. je Ri = 0,05 Ώ.
22.Jaký je odpor vnější části vedení, pokud vnitřní odpor vedení je 0,2 Ώ a elektromotorické napětí zdroje je 1,1 V. Voltmetr zapojen na svorky ukazuje 1V.
Řešení:
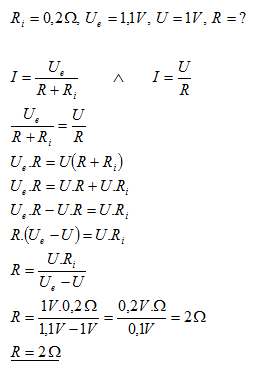
Odpor vnější části vedení je R = 2 Ώ.
23.Jak dlouhý železný drát (ρ = 0,1.10–6Ώm) s průřezem S = 0,2 mm2 je třeba připojit na článek s elektromotorickým napětím Ue = 2 V a vnitřním odporem Ri = 1 Ώ, aby obvodem procházel proud
I = 0,25A.
Řešení:
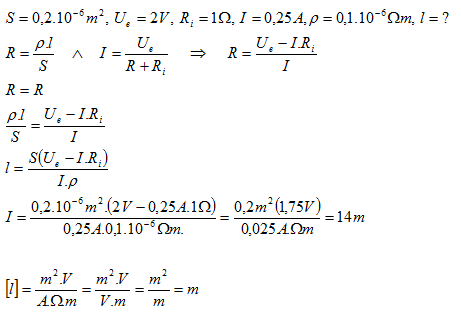
Na článek třeba připojit 14 m dlouhý drát.
24.Kolik zdrojů s Ue = 2 V a Ri = 0,2 Ώ je třeba spojit sériově, abychom při svorkovém napětí U = 120 V dostali v obvodu proud I = 2,5 A.
Řešení:
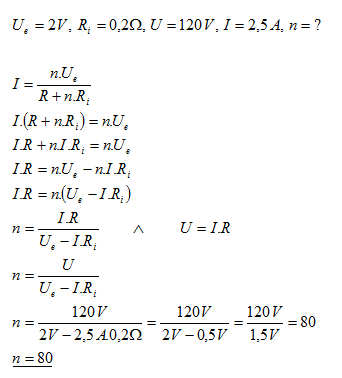
Je třeba zapojit 80 zdrojů.
25.Pokud na baterii s Ue = 4,5 V zapojíme vodič s odporem R = 2 Ώ, prochází jím proud I = 1,5 A. Jaký proud bude vodičem procházet při krátkém spojení?
Řešení:
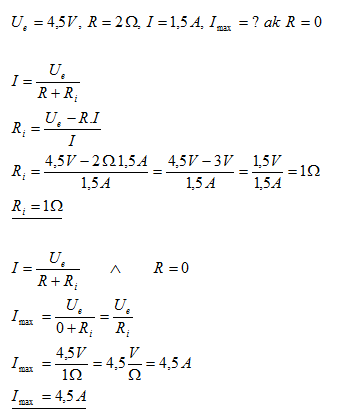
Při krátkém spojení bude řidičům procházet proud 4,5 A.
26.Galvanometr má základní rozsah Ug = 200 mV a Ig = 1mA.
- a.) Jaký rezistor Rp je třeba galvanometru předřadit, pokud jej chceme použít jako voltmetr s rozsahem Up = 10 V
- b.) Jaký rezistor RB připojíme ke galvanometru, abychom s galvanometrem mohli měřit proud do IB = 0,1A
Řešení:
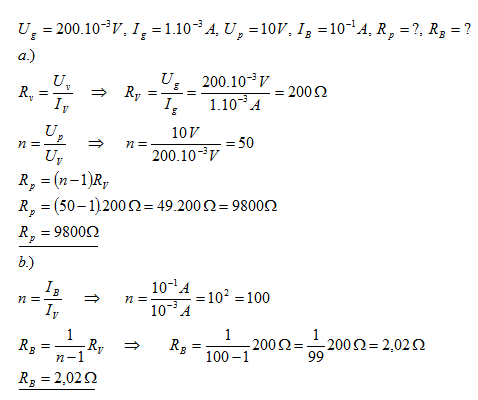
- a.) Odpor předřazeného rezistoru je Rp = 9800 Ώ.
- b.) Odpor bočníku je RB = 2,02 Ώ.
27.Ke zdroji elektromotorického napětí 15 V s vnitřním odporem 5Ώ je připojen rezistor s odporem 10Ώ. Ke svorkám zdroje napětí je paralelně připojen kondenzátor s kapacitou 1μF. Určitě náboj na kondenzátoru.
Řešení:
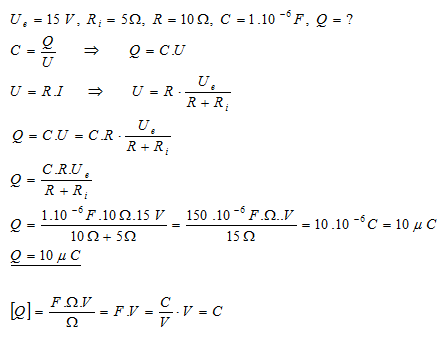
Náboj na kondenzátoru je Q = 10μC.
28.Vláknem wolframové žárovky s teplotou 00C prochází při napětí 10 V proud 0,3 A., při napětí 220 V proud 0,5 A, při čemž se vlákno zahřeje na 29760C. Určitě teplotní součinitel odporu wolframu.
Řešení:
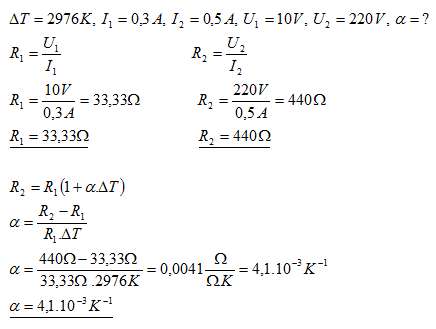
Teplotní součinitel odporu wolframu je α = 4,1.10–3K–1.
29.Když žárovka svítí, její wolframové drátek je zahřátý na teplotu 2500
0C. Žárovka je zapojena na napětí U = 220 V a prochází jí proud I = 0,272 A. Jaký je nárazový proud procházející žárovkou v okamžiku jejího zapojení? (Tj. při pokojové teplotě t
1 = 20
0C )
Řešení:
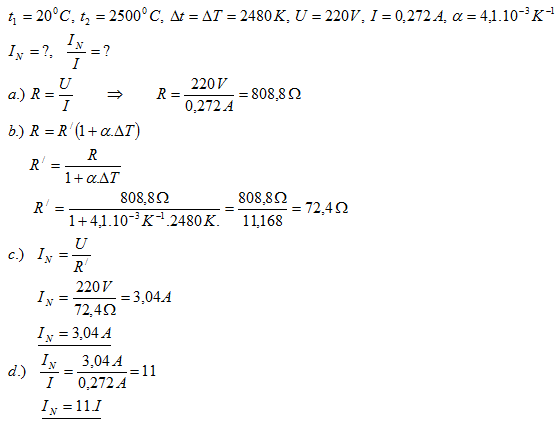
Nárazový proud při zapojení je asi 11-krát větší než proud zahřáté žárovky. Proto se často při zapojení vlákno žárovky propálí.