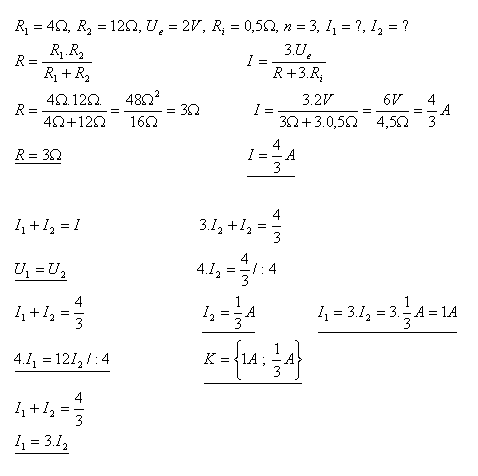Kirchhoffovy zákony
1. Vysvětlete použití Kirchhoffových zákonů v elektrotechnice.
Řešení:
Kirchhoffovy zákony se používají při řešení rozvětveného elektrického obvodu - (elektrické sítě), který má více zdrojů a rezistory jsou různé pospojovány. Uzel je místo v obvodu, kde se stýkají nejméně tři vodiče. Větev je část elektrického obvodu mezi dvěma uzly.

2.Proud 1,5 A se rozvětvuje do dvou paralelně zapojených rezistorů R1 = 4Ώ a R2 = 6Ώ. Jak velký proud je v každém rezistoru?
Řešení:
Rozbor:
I = 1,5A, R1 = 4Ώ , R2 = 6Ώ, I1 = ?, I2 = ?
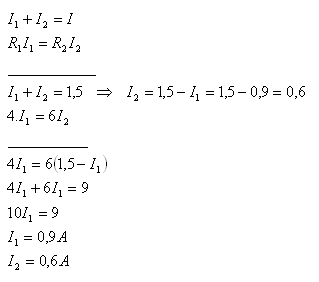
Rezistory procházejí proudy I1 = 0,9A, I2 = 0,6A.
3.Dva spotřebiče s odpory R1 = 400Ώ a R2 = 600Ώ jsou paralelně zapojeny a připojeny na napětí na napětí 300V. Určitě elektrické proudy procházející spotřebiči.
Řešení:
Rozbor:
R1 = 400Ώ, R2 = 600Ώ, U = 300V, R = ?, I = ?, I1 = ?, I2 = ?
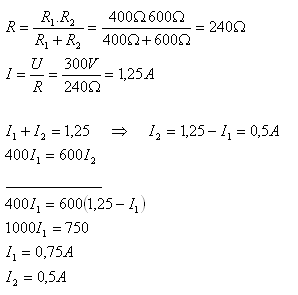
Spotřebiči procházejí proudy I1 = 075A a I2 = 0,5A.
4.Ampérmetr má rozsah 1,2 A a odpor 0,02 Ώ. Jaký musí být odpor bočníku, abychom mohli měřit proudy do 6A?
Řešení:
Rozbor:
I = 1,2A, RA = 0,02Ώ, I‘ = 6A, Rb = ?
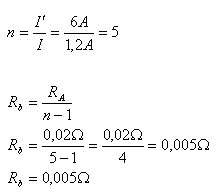
Odpor bočníku musí být Rb = 0,005Ώ.
5.Voltmetr je konstruován na maximální napětí 10V a chceme měřit napětí do 100V. Jaký bude odpor předřazeného rezistoru, pokud RV = 1kΏ?
Řešení:
Rozbor:
U‘ = 100V, U = 10V, RV = 1000Ώ, Rp = ?
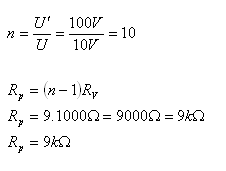
Odpor předřazeného rezistoru bude 9kΏ.
6. Dva rezistory s odpory R1 = 5Ώ a R2 = 10Ώ jsou spojeny paralelně a zapojené na konstantní napětí
U = 4,5 V. Vypočítejte výsledný odpor R, celkový proud I a proudy procházející jednotlivými rezistory.
Řešení:
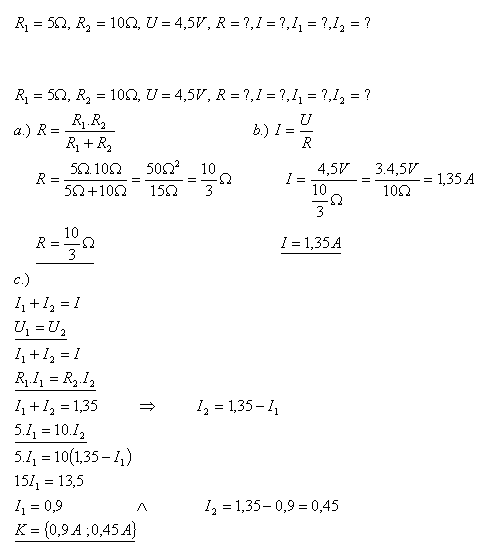
7.Tři rezistory jsou zapojeny do série. Úbytek napětí na rezistoru R1 = 36Ώ je U1 = 9V. Určete napětí U2 na rezistoru R2 = 64 Ώ a odpor R3, pokud napětí na svorkách zdroje je U = 120V.
Řešení:
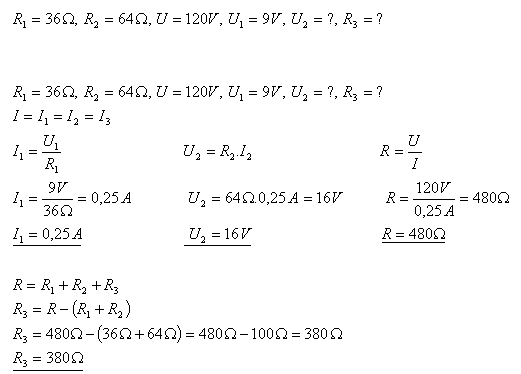
Na rezistoru R2 je napětí U2 = 16V. Třetí rezistor má odpor R3 = 380 Ώ.
8.Tři rezistory s odpory R1 = 15Ώ, R2 = 21Ώ a R3 = 14Ώ jsou spojeny sériově. Jaké je napětí na jednotlivých rezistorech, pokud celkové napětí zdroje je U = 40V. Jak velký proud prochází každým rezistorem?
Řešení:
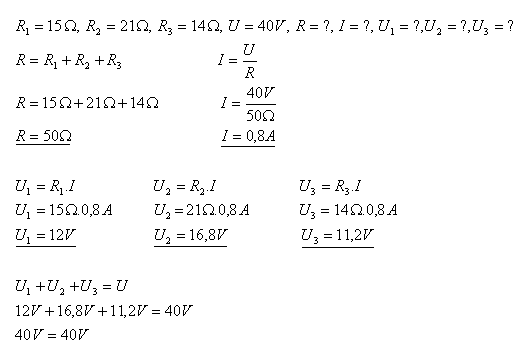
- Napětí na jednotlivých rezistorech jsou U1 = 12V, U2 = 16,8V, U3 = 11,2V.
- Každým rezistorem prochází proud 0,8 A.
9. Proud I = 4A se rozvětvuje do tří vodičů s odpory R1 = 2Ώ, R2 = 5Ώ, R3 = 10Ώ. Vypočítejte celkový odpor zapojení a napětí zdroje. Jak velké proudy jsou v jednotlivých vodičích?
Řešení:
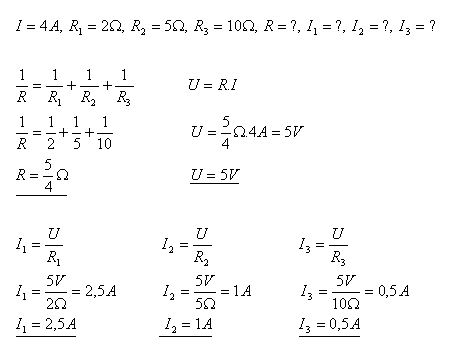
Proudy v jednotlivých vodičích jsou I1 = 2,5A, I2 = 1A, I3 = 0,5A.
10.Dva rezistory s odpory R1 a R3 jsou zapojeny sériově. Další dva R2 a R4 jsou zapojeny také sériově. Obě větve rezistorů jsou spojeny paralelně a zapojené na zdroj (Ue = 6V, Ri = 0,2 Ώ). Vypočítejte proudy procházející jednotlivými větvemi.
Řešení:
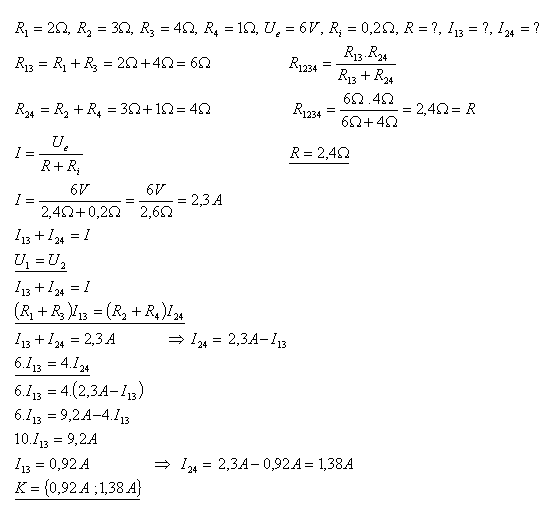
11.Ze zdroje s napětím Ue = 150V (Ri = 0) prochází proud rezistorem R1 = 38Ώ. Pak se větví do paralelně spojených rezistorů s odpory R2 = 20Ώ a R3 = 30Ώ. Vypočítejte proudy v jednotlivých větvích zapojení.
Řešení:
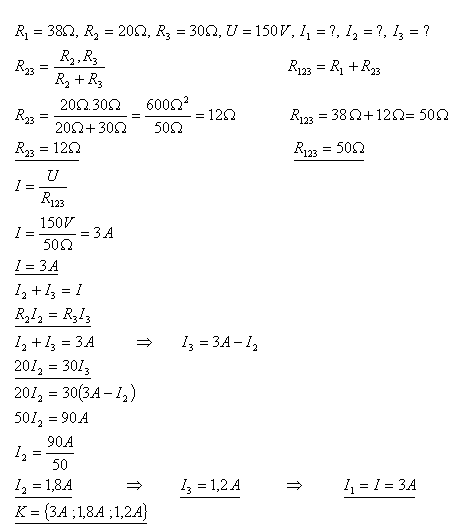
12.Dvě žárovky s příkony P1 = 45W a P2 = 5W jsou zapojeny paralelně ke zdroji, kterým prochází proud I = 3A. Určete proudy, které procházejí žárovkami.
Řešení:
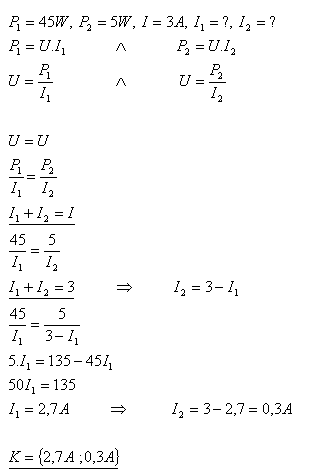
Jednotlivými žárovkami procházejí proudy I1 =2,7A a I2 = 0,3A.
13.Na kolik stejných částí třeba rozdělit drát s odporem R1 = 18Ώ, abychom je paralelním spojením dostali odpor R = 0,5 Ώ.
Řešení:
Rozbor:
R1 = 18Ώ, R = 0,5Ώ, n = ?
Odpor celého drátu R1, odpor jedné části drátu R = R1 / n Odpor paralelně spojených stejných částí drátu:
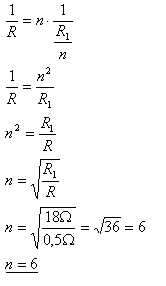
Drát třeba rozdělit na 6 stejných částí.
14.Jak velký proud je ve větvích, pokud R1 = 4Ώ, R2 = 12Ώ a když každý článek má elektromotorické napětí
Ue = 2V a vnitřní odpor Ri = 0,5 Ώ, n = 3
Řešení: