Špeciálna teória relativity
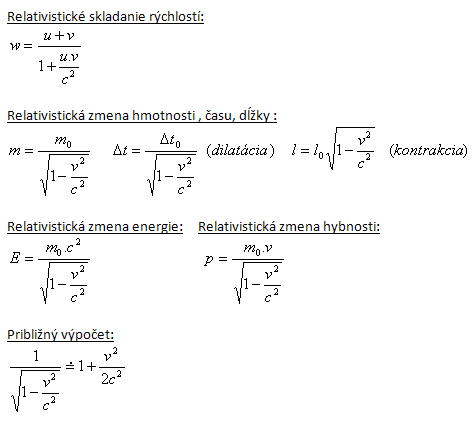
1. Vysvětlete rozdíl mezi klasickou fyzikou a speciální teorií relativity,
Řešení:
Klasická fyzika (Archimedes, Newton) zkoumá fyzikální vlastnosti těles, která jsou poměrně velká a pohybují se malými rychlostmi (v<<c). Považuje hmotnost, délku, čas, současnost dvou událostí, hybnost a energii za neměnné, nezávislé na rychlosti pohybu.
Speciální teorie relativity (Einstein) studuje pohyby těles, která se pohybují rychlostmi srovnatelnými s rychlostí světla ve vakuu c.
2.Ze zdroje elektronů vyletí opačnými směry dva elektrony. Každý elektron má rychlost v1 = v2 = 0,8c vzhledem k tomuto dělu. Jaká je jejich relativní rychlost?
Řešení:
Rozbor:
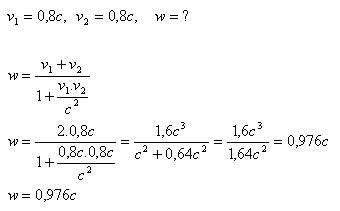
Relativní rychlost elektronů je w = 0,976c.
3.Částice α vyletěla z laboratorního urychlovače rychlostí v a pohybovala se rovnoměrně přímočaře. Trubicí o délce 12 cm proletěla za čas 1 ns. Jakou délku má trubice ve vztažné soustavě spojené s částicí α?
Řešení:
Rozbor:
s = 12 cm = 0,12 m, t = 1 ns = 10-9s, l = ?
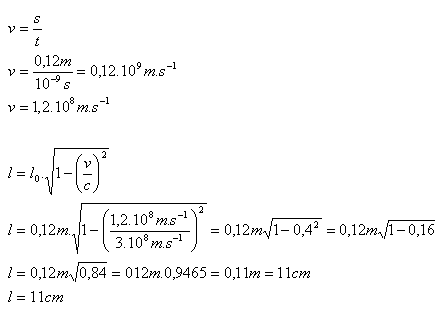
Délka trubice urychlovače se zmenšila na 11 cm.
4.Z urychlovače vyletuje svazek π mezonů rychlostí v = 0,8c. Poločas rozpadu π mezonů je t0 = 1,8.10-8s. Vypočítejte, za jakou dobu se rozpadne polovina mezonů a jakou dráhu uletí, než se rozpadnou.
Řešení:
Rozbor:
v = 0,8c, t0 = 1,8.10-8 s, t = ?, s = ?
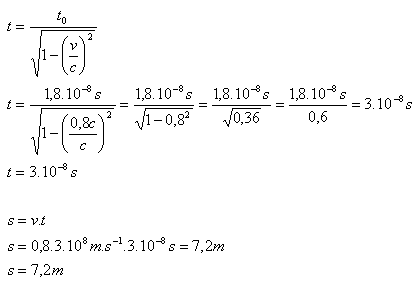
Polovina mezonů se rozpadne za t = 3.10–8s. Při tom uletí dráhu s = 7,2 m.
5.Hustota železa je ρ0 = 7400 kg.m-3 v nehybné soustavě. Jak se změní hustota tělesa ze železa, pokud se jeho rychlost zvýší z nulové hodnoty na v = 0,5c?
Řešení:
Rozbor:
ρ0 = 7400 kg.m-3, v = 0,5c, ρ = ?
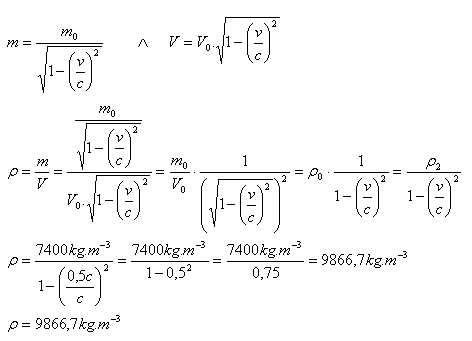
Hustota tělesa se změní na ρ = 9866,7 kg.m-3.
6.Vypočítejte rychlost, při které je relativistická hybnost částice α dvakrát větší než hybnost vypočtená podle pravidel klasické mechaniky.
Řešení:
Rozbor:
2p0 = p
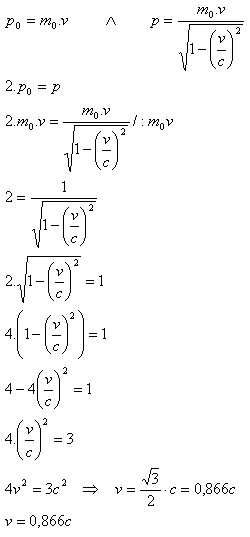
Rychlost částice α je v = 0,866c
7.Kosmická loď se pohybuje vzhledem k Zemi rychlostí 12 000 km.s-1. Jak dlouho trvá pro pozorovatele v kosmické lodi děj, který na Zemi probíhá 1 hodinu.
Řešení:
Rozbor:
v = 12 000 km.s-1 = 1,2.107 m.s-1, t0 = 1 hod., t = ?
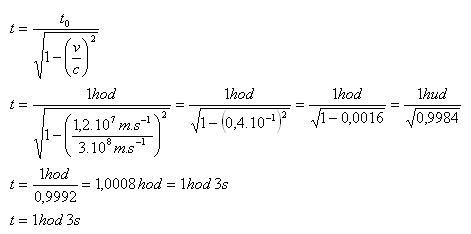
Pro pozorovatele v kosmické lodi trvá děj asi 1 hodinu a 3 sekundy.
8.Jakou vlnovou délku má foton, jehož energie je stejná jako energie elektronu při rychlosti v = 0,6c?
Řešení:
Rozbor:
v = 0,6c, c = 3.108 m.s-1, h = 6,625.10-34 J.s, me = 9,1.10-31 kg, λ = ?,
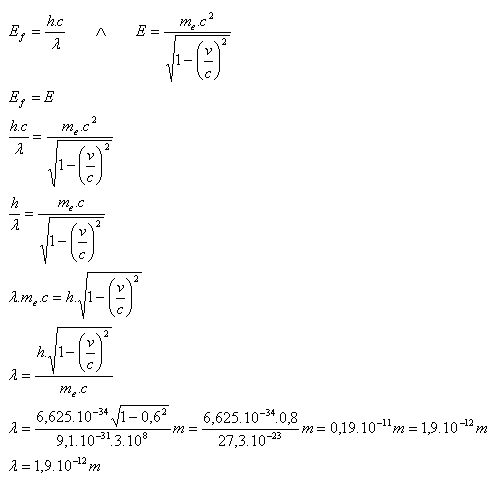
Vlnová délka fotonu je f = 1,9.10-12 m.
9.Hvězda se přibližuje k Zemi rychlostí v. Jakou rychlostí se světlo z této hvězdy šíří vesmírem pro pozorovatele na Zemi?
Řešení:
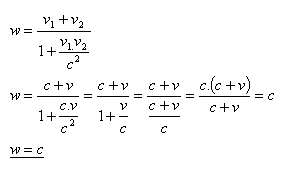
Světlo z této hvězdy se šíří vesmírem pro pozorovatele na Zemi rychlostí w = c = 3.108 m.s–1.
10.V „kosmickém vlaku“, který se řítí vesmírem rychlostí v1 = c/2, se pohybuje kosmonaut rychlostí v2 = c/4 podél „vlaku“. Jakou rychlost zjistí pozorovatel stojící mimo „vlak“, pokud se kosmonaut pohybuje
- a.) týmž směrem jako „vlak“
- b.) opačným směrem než „vlak“
Řešení:
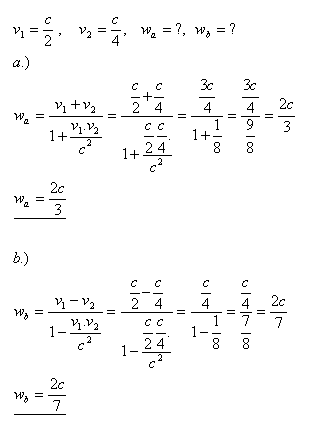
Pozorovatel stojící mimo „vlak“ zjistí rychlosti 2c/3, nebo 2c/7.
11.Hyperon se pohybuje v bublinkové komoře rychlostí v1 = 0,8c a při jeho přeměně na proton, elektron a antineutrino vyšle ve směru svého pohybu proton, který se v klidové soustavě hyperonu pohybuje rychlostí v2 = 0,3c. Jakou rychlostí se bude pohybovat proton vzhledem k souřadnicové soustavě spojené s bublinkovou komorou, jestliže
- a.) neplatí relativistický vztah pro skládání rychlostí
- b.) platí relativistický vztah pro skládání rychlostí
Řešení:
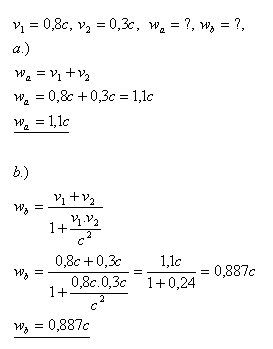
Proton se bude pohybovat rychlostí 0,887c.
Rychlost 1,1c > c neexistuje.
12. Vyučovací hodina na Zemi trvá 45 minut. Kolik minut by trvala vyučovací hodina na kosmické lodi, která se vzdaluje od Země rychlostí v = 0,6c?
Řešení:
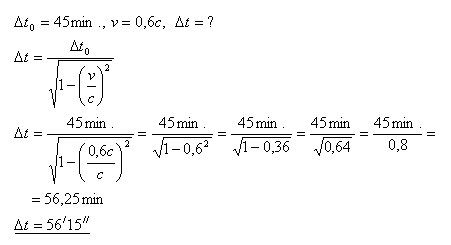
Vyučovací hodina na kosmické lodi by trvala 56 minut a 15 sekund.
13.Jakou rychlost musí mít raketa vzhledem k Zemi, aby jistý děj pozorovaný na Zemi pozoroval kosmonaut na raketě jako dvojnásobně dlouhý.
Řešení:
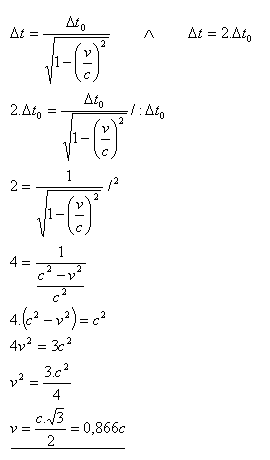
Raketa musí mít rychlost v = 0,866c.
14.Střední doba životnosti mezonu je Δt0 = 2,2.10–6s. Vypočítejte dráhu, kterou projde mezon od svého vzniku po rozpad na elektron a neutrino. Mezon se pohybuje rychlostí v = 0,96c.
Řešení:
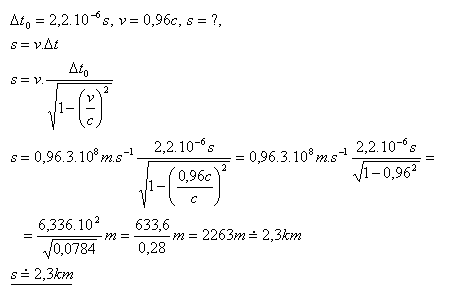
Mezon během doby své životnosti uletí dráhu asi 2,3 km.
15.Vzdálenost hvězdy Proxima Centauri od Země je 4,28 ly (světelných let). Jakou vzdálenost zjistí pozorovatel v kosmické lodi, která letí ze Země ke hvězdě rychlostí v = 0,8c vzhledem k Zemi.
Řešení:
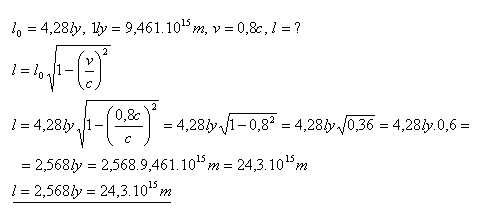
Pozorovatel na kosmické lodi zjistí vzdálenost hvězdy od Země l = 2,568 ly. Je to 24,3.1015 metru.
16.Těleso, které má v klidové soustavě tvar krychle, se pohybuje ve směru osy x rovnoměrně přímočaře rychlostí v = 0,95c kolmo na stěnu krychle. Klidová délka krychle je a0 = 1 m. Určete objem tělesa ve vztažné soustavě, vůči níž se těleso pohybuje.
Řešení:
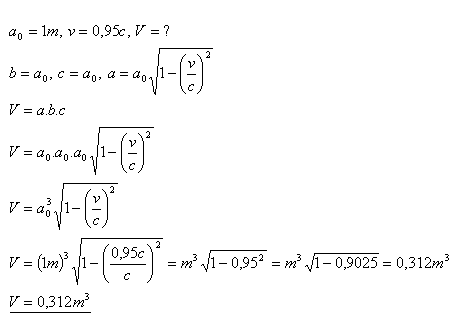
Objem tělesa pohybujícího se rychlostí 0,95c je V = 0,312 m3.
17.Jaká byla klidová délka tyče, která se pohybuje vzhledem k pozorovateli, jenž je v klidu, rychlostí v = 2,7.108 m.s–1. Pozorovateli se jeví tato tyč jako 2,61 m dlouhá.
Řešení:
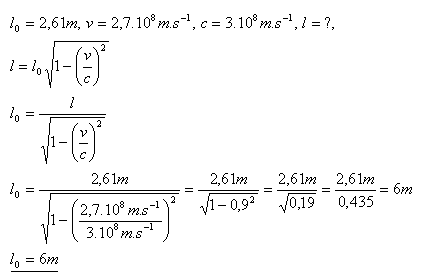
Klidová délka tyče byla l0 = 6 metrů.
18. Elementární částice se pohybuje rychlostí v = 0,8c. Jaký je poměr její hmotnosti k její klidové hmotnosti?
Řešení:
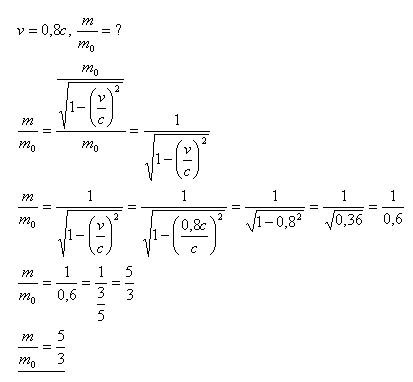
Poměr hmotností elementární částice je m : m0 = 5 : 3.
19.Elektron byl cyklotronem urychlen tak, že jeho relativistická hmotnost nabyla hodnoty 5krát větší, než je jeho klidová hmotnost. Jakou rychlostí se elektron pohybuje?
Řešení:
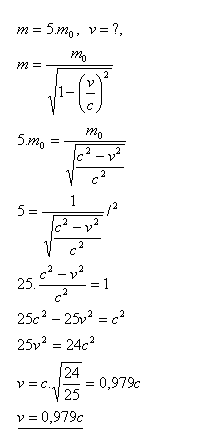
Rychlost elektronu je v = 0,979c.
20.Odvoďte relativistický vztah:
Řešení:
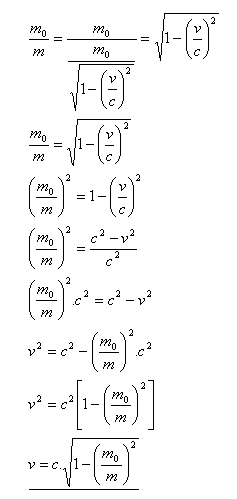
21.Proton má klidovou energii E0 = 933 MeV a pohybuje se rychlostí v = 0,5c. Vypočítejte jeho relativistickou kinetickou energii.
Řešení:
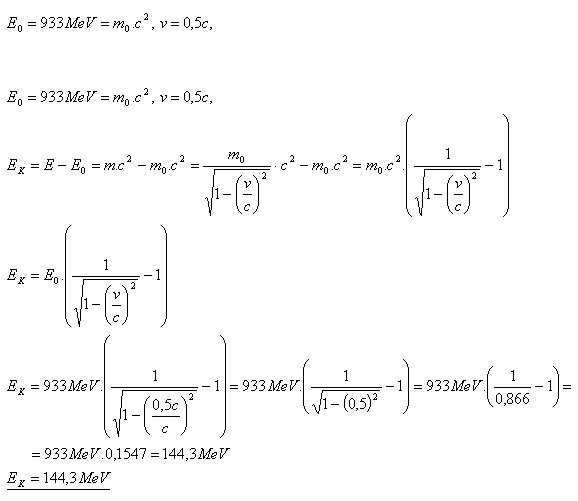
Relativistická kinetická energie protonu je EK = 144,3 MeV.
22.Při jaké rychlosti se kinetická energie částice rovná její klidové energii?
Řešení:
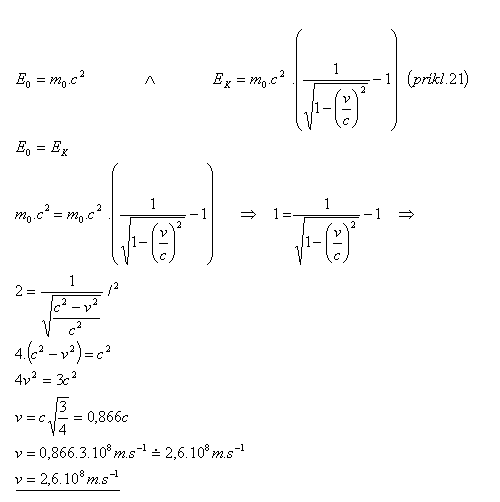
Kinetická energie částice se rovná její klidové energii při rychlosti v = 2,6.108 m.s–1.
23.Hmotnost urychleného elektronu se zvětšila 41krát. Jakou energii získal elektron při tomto zrychlení?
Řešení:
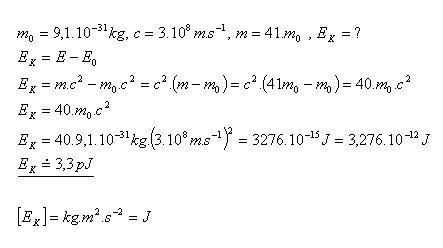
Elektron urychlením získal kinetickou energii EK = 3,3 pJ.
24.Jakou vlnovou délku má foton, jehož energie je stejná jako klidová energie elektronu?
Řešení:
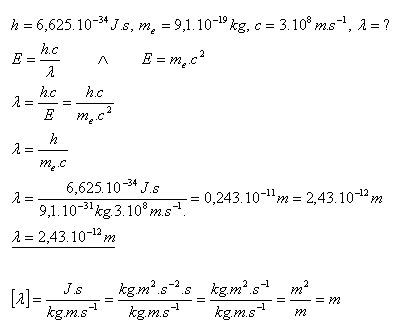
Vlnová délka fotonu je λ = 2,43.10–12 m.
25. Elektron s klidovou hmotností m0 = 9,1.10–31 kg se pohybuje rychlostí v = 0,6c. Vypočítejte relativistickou hybnost tohoto elektronu.
Řešení:
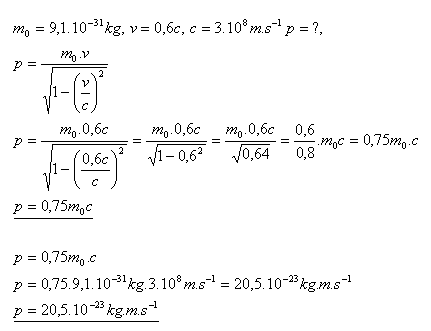
Hybnost elektronu je p = 20,5.10–23 kg.m.s–1.