Spezielle Relativitätstheorie

1. Erklären Sie den Unterschied zwischen der klassischen Physik und der speziellen Relativitätstheorie,

Lösung:

Die klassische Physik (Archimedes, Newton) untersucht die physikalischen Eigenschaften von Körpern, die relativ groß sind und sich mit niedrigen Geschwindigkeiten bewegen (v << c). Sie betrachtet Masse, Länge, Zeit, Gleichzeitigkeit zweier Ereignisse, Impuls und Energie als konstant und unabhängig von der Bewegungsgeschwindigkeit.

Die spezielle Relativitätstheorie (Einstein) untersucht die Bewegung von Körpern, die sich mit Geschwindigkeiten bewegen, die mit der Lichtgeschwindigkeit im Vakuum c vergleichbar sind.

Relativistisches Addieren von Geschwindigkeiten:

w = \frac{u + v}{1 + \frac{u v}{c^{2}}}

Relativistische Änderung von Masse, Zeit, Länge:

$m = \frac{m_0}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}$ $\Delta t = \frac{\Delta t_0}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \quad (\text{Dilatation})$

$l = l_0 \sqrt{1 - \frac{v^{2}}{c^{2}}} \quad (\text{Kontraktion})$

Relativistische Änderung der Energie:

E = \frac{m_0 c^{2}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}

Relativistische Änderung des Impulses:

p = \frac{m_0 v}{\sqrt{1 - \frac{v^{2}}{c^{2}}}}

Näherungsberechnung:

\frac{1}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} \approx 1 + \frac{1}{2}\frac{v^{2}}{c^{2}

2. Aus einer Elektronenquelle fliegen zwei Elektronen in entgegengesetzte Richtungen heraus. Jedes Elektron hat relativ zu dieser Kanone eine Geschwindigkeit v₁ = v₂ = 0.8c. Wie groß ist ihre Relativgeschwindigkeit?

Lösung:

Analyse:

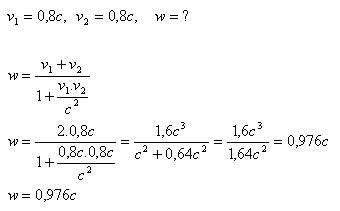
Die Relativgeschwindigkeit der Elektronen beträgt w = 0.976c.

3. Ein α-Teilchen flog aus einem Laborbeschleuniger mit der Geschwindigkeit v aus und bewegte sich gleichförmig geradlinig. Es durchlief ein Rohr von 12 cm Länge in 10 ns. Wie lang ist das Rohr im Bezugssystem des α-Teilchens?

Lösung:

Analyse:

s = 12 cm = 0.12 m, t = 10 ns = 10^-9s, l = ?

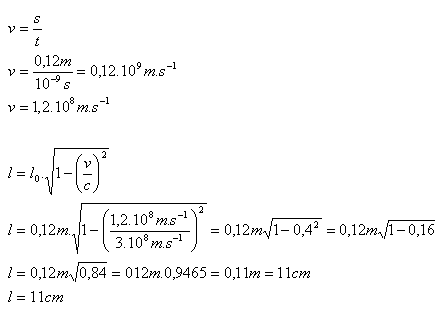
Die Länge des Beschleunigerrohres verkürzt sich auf 11 cm.

4. Ein Strahl von π-Mesonen fliegt mit v = 0.8c aus einem Beschleuniger. Die Halbwertszeit der π-Mesonen beträgt t₀ = 1.8·10^-8s. Berechnen Sie die Zeit, nach der die Hälfte der Mesonen zerfallen ist, und die Entfernung, die sie bis zum Zerfall zurücklegen.

Lösung:

Analyse:

v = 0.8c, t₀ = 1.8·10^-8s, t = ?, s = ?

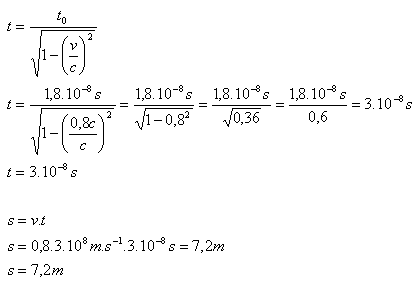
Die Hälfte der Mesonen zerfällt nach t = 3·10^–8s. In dieser Zeit legen sie eine Strecke s = 7.2 m zurück.

5. Die Dichte von Eisen beträgt im Ruhesystem ρ₀ = 7400 kg·m^-3. Wie ändert sich die Dichte eines Eisenkörpers, wenn seine Geschwindigkeit von 0 auf v = 0.5c erhöht wird?

Lösung:

Analyse:

ρ₀ = 7400 kg·m^-3, v = 0.5c, ρ = ?

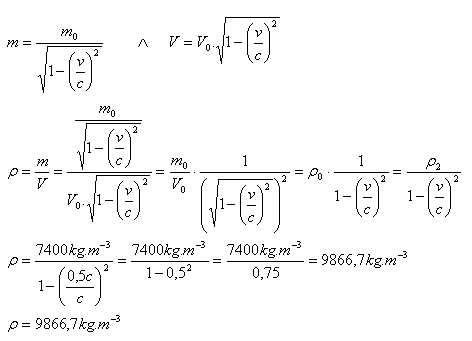
Die Dichte des Körpers ändert sich zu ρ = 9866.7 kg·m^-3.

6. Berechnen Sie die Geschwindigkeit, bei der der relativistische Impuls eines α-Teilchens doppelt so groß ist wie der klassisch berechnete Impuls.

Lösung:

Analyse:

2p₀ = p

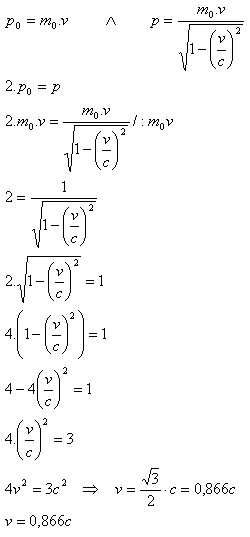
Die Geschwindigkeit des α-Teilchens beträgt v = 0.866c

7. Ein Raumschiff bewegt sich relativ zur Erde mit 12.000 km·s^-1. Wie lange dauert ein Ereignis, das auf der Erde 1 Stunde dauert, für einen Beobachter im Raumschiff?

Lösung:

Analyse:

v = 12.000 km·s^-1 = 1.2·10⁷ m·s^-1, t₀ = 1 Stunde, t = ?

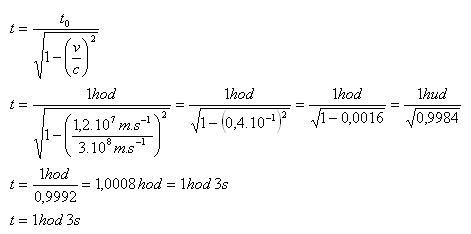
Für den Beobachter im Raumschiff dauert das Ereignis etwa 1 Stunde und 3 Sekunden.

8. Wie groß ist die Wellenlänge eines Photons, dessen Energie der Energie eines Elektrons entspricht, das sich mit v = 0.6c bewegt?

Lösung:

Analyse:

v = 0.6c, c = 3·10⁸ m·s^-1, h = 6.625·10^-34 J·s, m_e = 9.1·10^-31 kg, λ = ?,

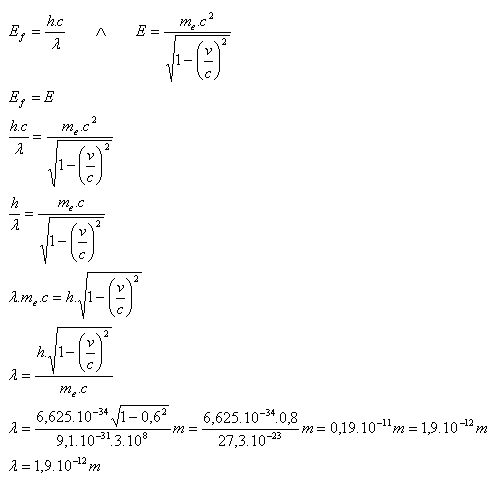
Die Wellenlänge des Photons beträgt λ = 1.9·10^-12 m.

9.Der Stern nähert sich der Erde mit der Geschwindigkeit v. Mit welcher Geschwindigkeit bewegt sich das Licht dieses Sterns für einen Beobachter auf der Erde durch den Raum?

Lösung:

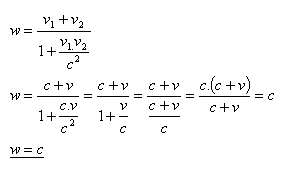
Das Licht dieses Sterns bewegt sich für einen Beobachter auf der Erde mit der Geschwindigkeit w = c = 3·10⁸ m·s^–1.

10.In einem „kosmischen Zug“, der sich mit v₁ = c/2 durch den Raum bewegt, bewegt sich ein Astronaut mit v₂ = c/4 entlang des „Zuges“. Welche Geschwindigkeit misst ein Beobachter außerhalb des „Zuges“, wenn sich der Astronaut

a.) in dieselbe Richtung wie der „Zug“ bewegt
b.) in die entgegengesetzte Richtung zum „Zug“ bewegt

Lösung:

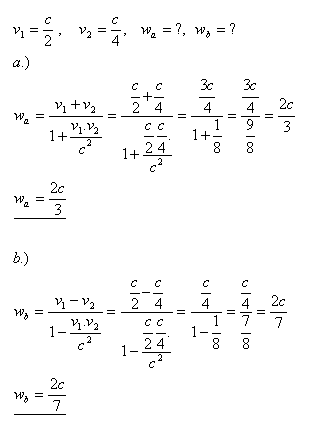
Der Beobachter außerhalb des „Zuges“ misst Geschwindigkeiten von 2c/3 bzw. 2c/7.

11.Ein Hyperon bewegt sich in einer Blasenkammer mit v₁ = 0.8c und emittiert beim Zerfall in Proton, Elektron und Antineutrino in Bewegungsrichtung ein Proton, das sich im Ruhesystem des Hyperons mit v₂ = 0.3c bewegt. Welche Geschwindigkeit hat das Proton im Bezugssystem der Blasenkammer, wenn

a.) die relativistische Geschwindigkeitsaddition nicht gilt
b.) die relativistische Geschwindigkeitsaddition gilt

Lösung:

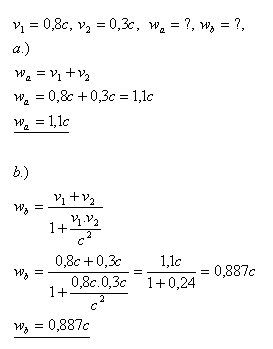
Das Proton bewegt sich mit der Geschwindigkeit 0.887c.

Die Geschwindigkeit 1.1c > c existiert nicht.

12.Eine Schulstunde auf der Erde dauert 45 Minuten. Wie viele Minuten würde die Stunde auf einem Raumschiff dauern, aus Sicht eines Beobachters auf der Erde, wenn sich das Raumschiff mit v = 0.6c von der Erde entfernt?

Lösung:

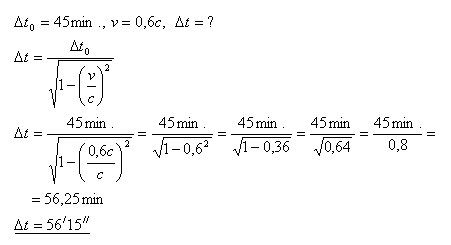
Die Stunde auf dem Raumschiff würde aus Sicht des Beobachters auf der Erde 56 Minuten und 15 Sekunden dauern.

13.Welche Geschwindigkeit muss eine Rakete relativ zur Erde haben, damit ein bestimmter Prozess, der auf der Erde beobachtet wird, vom Astronauten in der Rakete doppelt so lange beobachtet wird?

Lösung:

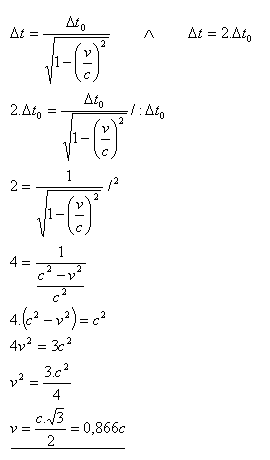
Die Rakete muss eine Geschwindigkeit v = 0.866c haben.

14.Die mittlere Lebensdauer eines Mesons beträgt Δt₀ = 2.2·10^–6 s. Berechnen Sie die Strecke, die das Meson von seiner Entstehung bis zu seinem Zerfall in Elektron und Neutrino zurücklegt. Das Meson bewegt sich mit v = 0.96c.

Lösung:

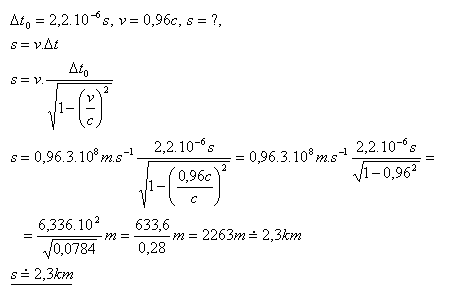
Während seiner Lebensdauer legt das Meson eine Strecke von etwa 2.3 km zurück.

15.Die Entfernung des Sterns Proxima Centauri von der Erde beträgt 4.28 Lj (Lichtjahre). Welche Entfernung misst ein Beobachter in einem Raumschiff, das sich mit v = 0.8c relativ zur Erde zum Stern bewegt?

Lösung:

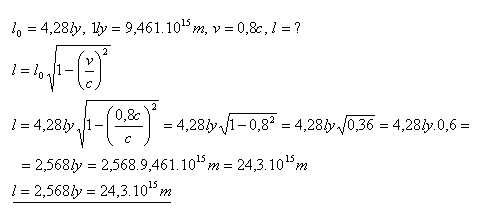
Der Beobachter im Raumschiff misst die Entfernung zum Stern als l = 2.568 Lj. Das sind 24.3·10¹⁵ Meter.

16.Ein Körper, der im Ruhesystem die Form eines Würfels hat, bewegt sich gleichförmig in Richtung der x-Achse mit v = 0.95c senkrecht zu einer Würfelfläche. Die Ruhelänge des Würfels beträgt a₀ = 1 m. Bestimmen Sie das Volumen des Körpers im Bezugssystem, relativ zu dem sich der Körper bewegt.

Lösung:

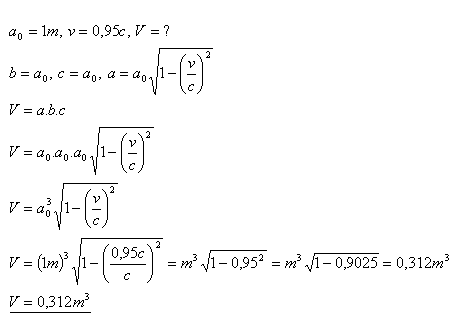
Das Volumen des Körpers, der sich mit 0.95c bewegt, beträgt V = 0.312 m³.

17.Wie groß war die Ruhelänge einer Stange, die sich relativ zu einem ruhenden Beobachter mit v = 2.7·10⁸ m·s^–1 bewegt? Der Beobachter sieht die Stange als 2.61 m lang.

Lösung:

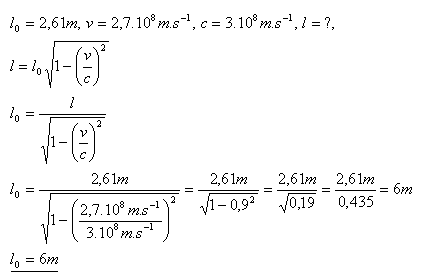
Die Ruhelänge der Stange betrug l₀ = 6 Meter.

18.Ein Elementarteilchen bewegt sich mit v = 0.8c. Wie groß ist das Verhältnis seiner Masse zu seiner Ruhemasse?

Lösung:

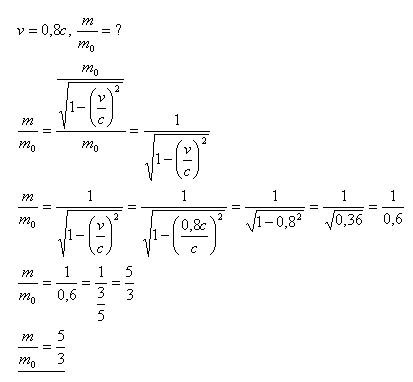
Das Massenverhältnis des Elementarteilchens beträgt m : m₀ = 5 : 3.

19.Ein Elektron wurde im Zyklotron so stark beschleunigt, dass seine relativistische Masse fünfmal so groß wie seine Ruhemasse wurde. Welche Geschwindigkeit hat das Elektron?

Lösung:

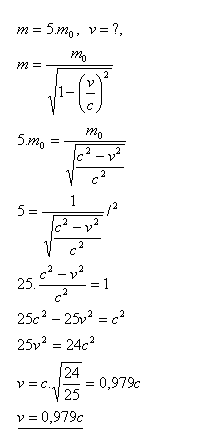
Die Geschwindigkeit des Elektrons beträgt v = 0.979c.

20.Leiten Sie die relativistische Beziehung her:

Lösung:

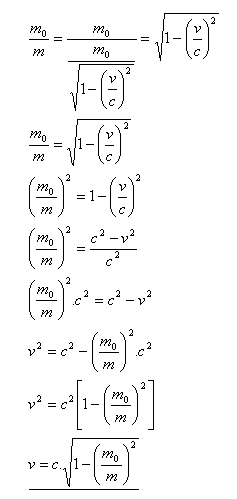
21.Ein Proton hat die Ruheenergie E⁰ = 933 MeV und bewegt sich mit v = 0.5c. Berechnen Sie seine relativistische kinetische Energie.

Lösung:

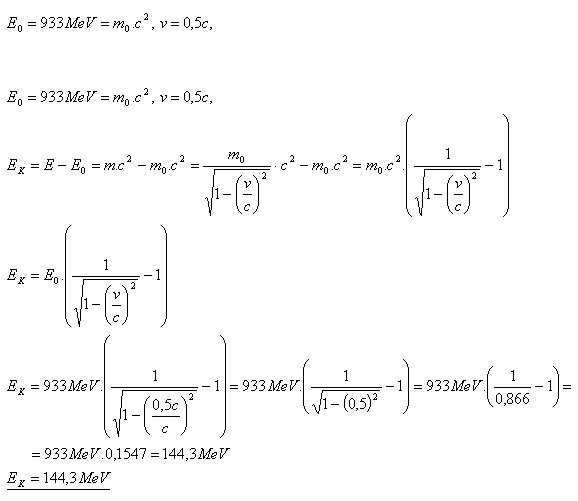
Die relativistische kinetische Energie des Protons beträgt E_K = 144.3 MeV.

22.Bei welcher Geschwindigkeit ist die kinetische Energie eines Teilchens gleich seiner Ruheenergie?

Lösung:

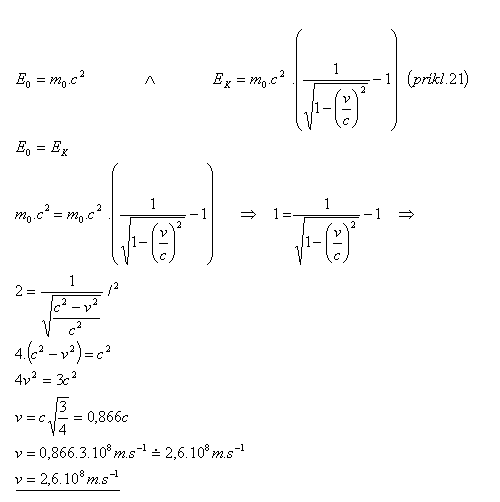
Die kinetische Energie entspricht der Ruheenergie bei einer Geschwindigkeit von v = 2.6·10⁸ m·s^–1.

23.Die Masse eines beschleunigten Elektrons hat sich 41-fach vergrößert. Welche Energie hat das Elektron während dieser Beschleunigung aufgenommen?

Lösung:

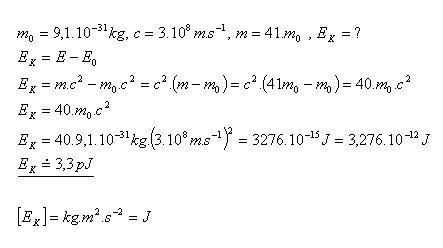
Durch die Beschleunigung hat das Elektron eine kinetische Energie E_K = 3.3 pJ aufgenommen.

24.Wie groß ist die Wellenlänge eines Photons, dessen Energie der Ruheenergie eines Elektrons entspricht?

Lösung:

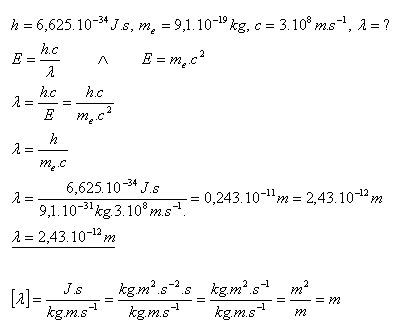
Die Wellenlänge des Photons beträgt λ = 2.43·10^–12 m.

25.Ein Elektron mit der Ruhemasse m₀ = 9.1·10^–31 kg bewegt sich mit v = 0.6c. Berechnen Sie den relativistischen Impuls dieses Elektrons.

Lösung:

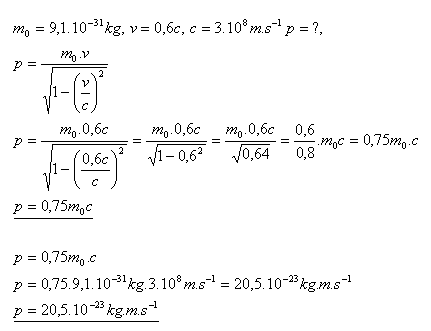
Der Impuls des Elektrons beträgt p = 20.5·10^–23 kg·m·s^–1.

Physik

Spezielle Relativitätstheorie

Adblock detected