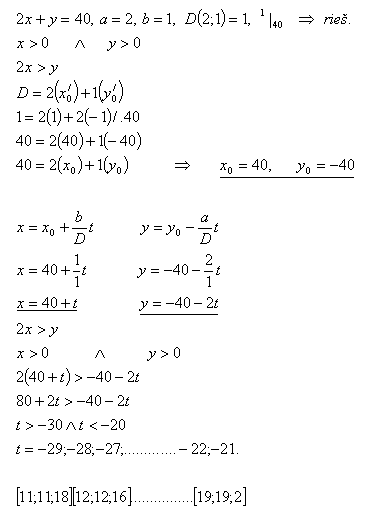Diophantische Gleichungen
1. Löse die Gleichungen:
ax + by = 0 und ax + by = c
Lösung:
Der griechische Mathematiker DIOPHANTUS (etwa 250 v. Chr.) beschäftigte sich mit dem Lösen von Gleichungen der Form ax + by = c, wobei nur ganzzahlige Lösungen akzeptiert wurden. Solche Gleichungen nennt man „diophantische Gleichungen“.
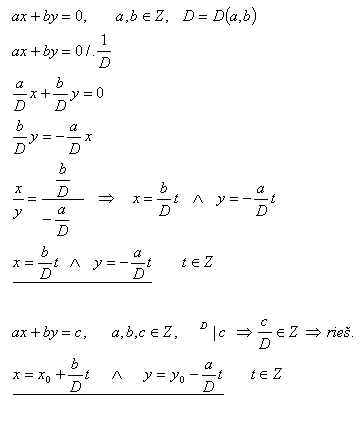
2.In der Menge Z löse die Gleichung:
6x – 4y = 0
Lösung:
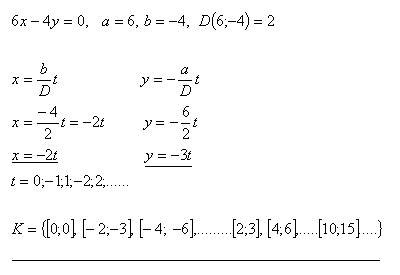
3.In der Menge Z löse die Gleichung:
3x + 15y = 0
Lösung:
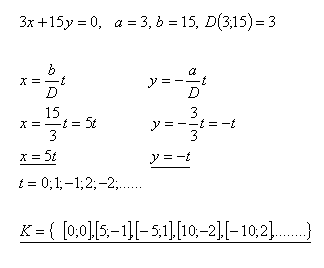
4.Finde heraus, welche der folgenden Gleichungen in der Menge Z lösbar sind:
Lösung:
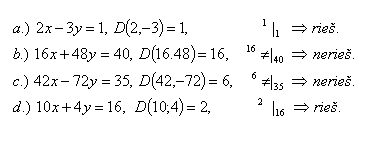
5.In der Menge Z löse die Gleichung:
10x + 4y = 16
Lösung:
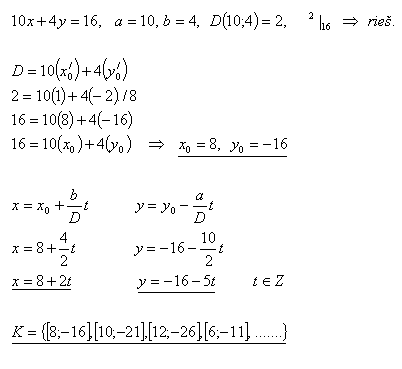
6.In der Menge Z löse die Gleichung:
21x + 15y = 3
Lösung:
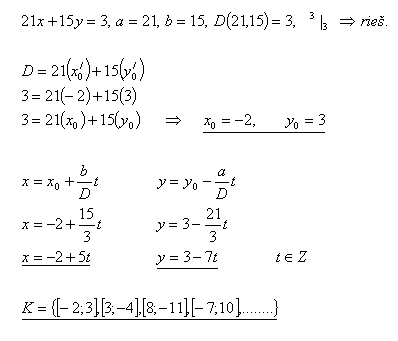
7.Welche ganzzahligen Abmessungen kann ein Rechteck haben, wenn sein Umfang 24 cm beträgt?
Lösung:
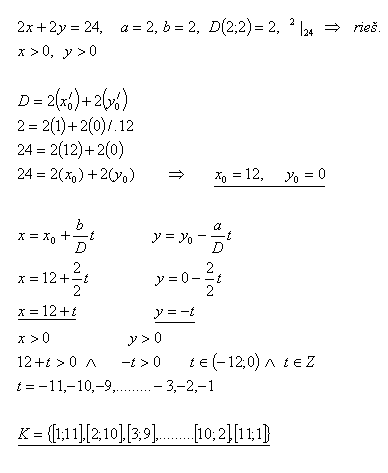
8.Auf welche Arten kann man die Summe von 21 Euro bezahlen, wenn man nur 2-Euro- und 5-Euro-Münzen hat?
Lösung:
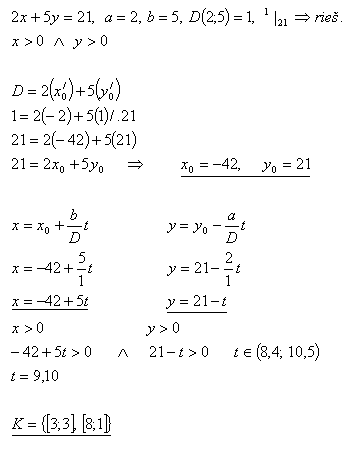
9.Bestimme, auf wie viele Arten 22 Liter Wein in 2-Liter- und 3-Liter-Gefäße abgefüllt werden können.
Lösung:
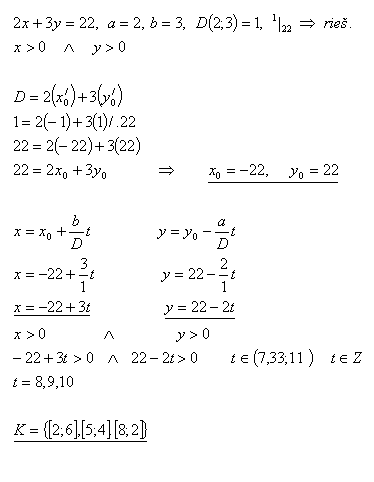
10.Ein 50 cm langes Band soll in Stücke von 6 cm und 4 cm Länge geschnitten werden. Auf wie viele Arten kann dies geschehen?
Lösung:
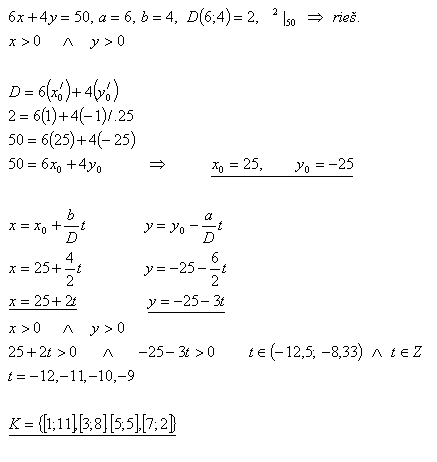
11.Bestimme alle gleichschenkligen Dreiecke, deren Seitenlängen ganze Zahlen sind und deren Umfang 40 cm beträgt.
Lösung: