Permutationen
1. Definieren und charakterisieren Sie:
a) Permutationen aus n Elementen
b) Permutationen aus n Elementen mit Wiederholungen
Lösung:
Permutationen
Eine Permutation ist eine Folge, die jedes Element einer endlichen Menge von n Elementen genau einmal enthält. Permutationen derselben Menge unterscheiden sich nur in der Reihenfolge der Elemente.
P(n) = n!
Permutationen mit Wiederholungen
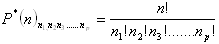
n1 – Anzahl der gleichen Elemente der ersten Kategorie
n2 - Anzahl der gleichen Elemente der zweiten Kategorie
n3 - Anzahl der gleichen Elemente der dritten Kategorie
nj - Anzahl der gleichen Elemente der j-ten Kategorie
Es gilt: n1+n2+n3+.........+nj = n
2. Es gibt 3 Elemente a, b, c. Bilden Sie daraus:
a) Permutationen (ohne Wiederholung)
b) Permutationen mit Wiederholung, wobei „a“ zweimal, „b“ einmal und „c“ einmal vorkommt
Lösung:
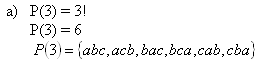
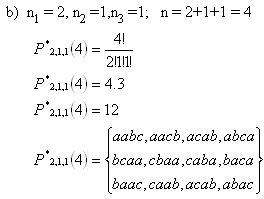
3.Wie viele positive ganze Zahlen mit 5 Ziffern können aus den Ziffern 1,2,3,4,5 gebildet werden, wenn:
a) jede Ziffer nur einmal verwendet werden darf?
b) wie viele davon mit 5 beginnen?
c) wie viele davon gerade sind?
Lösung:
a) P(5) = 5! = 5·4·3·2·1 = 120
b) P(4) = 4! = 4·3·2·1 = 24
c)
endet mit 2: P(4) = 4! = 24
endet mit 4: P(4) = 4! = 24
Summe : S = 2·4! = 2·24 = 48
4.Acht Studenten sollen in zwei Dreibett- und einem Zweibettzimmer untergebracht werden. Auf wie viele Arten können sie untergebracht werden?
Lösung:
Zimmer Nr. 1: n1 = 3
Zimmer Nr. 2: n2 = 3
Zimmer Nr. 3: n3 = 2
n = 3 + 3 + 2 = 8
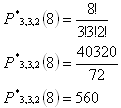
Es gibt 560 Möglichkeiten, die Studenten unterzubringen.
5.Auf wie viele Arten kann man mit drei Würfeln die Summe 11 werfen?
Lösung:
a) Permutation des Tripels 6,4,1 : P(3) = 3! = 6
b) Permutation des Tripels 6,3,2 : P(3) = 3! = 6
c) Permutation des Tripels 5,5,1 : P2,1*(3) = 3
d) Permutation des Tripels 5,4,2 : P(3) = 3! = 6
e) Permutation des Tripels 5,3,3 : P*1,2(3) = 3
f) Permutation des Tripels 4,4,3 : P*2,1(3) = 3
Summe 6+6+3+6+3+3 = 27 Möglichkeiten.
6.Es gibt 4 tschechische und 3 slowakische Bücher im Bücherregal. Die tschechischen Bücher sollen auf der linken Seite und die slowakischen auf der rechten Seite stehen. Auf wie viele Arten können die Bücher angeordnet werden?
Lösung:
Anordnung der tschechischen Bücher: P(4) = 4! = 24
Anordnung der slowakischen Bücher: P(3) = 3! = 6
N = P(4)·P(3) = 24·6 = 144
Die Bücher können auf 144 Arten angeordnet werden.
7. Wenn die Anzahl der Elemente um 2 steigen würde, würde die Anzahl der Permutationen ohne Wiederholung um das 42-fache steigen. Wie viele Elemente gibt es?
Lösung:
P(x + 2) = 42·P(x)
(x + 2)! = 42·x!
(x + 2)(x +1)x! = 42x!/: x!
(x + 2)(x + 1) = 42
x2 + 3x + 2 - 42 = 0
x2 + 3x – 40 = 0
(x – 5)(x + 8) = 0
x1 = 5
x2 = - 8 entfällt
K={5}
Es gibt 5 Elemente.
8.Zählen Sie alle möglichen Anordnungen von 15 Personen auf einem Foto.
a) Wie viele Fotos werden gemacht?
b) Wie lange würde das Fotografieren dauern, wenn ein Foto 10 Sekunden dauert?
Lösung:
a)
P(15) = 15! = 1,307·10
12
1,307·10
12 Fotos werden gemacht.
b)
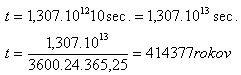
Das Fotografieren würde 414 377 Jahre dauern.
9.Ein Passwort aus 6 Ziffern wird aus den Ziffern 926002 gebildet.
Wie viele mögliche Passwörter gibt es?
Wie lange würde es dauern, alle möglichen Passwörter zu probieren, wenn das Testen eines Passworts 5 Sekunden dauert?
Lösung:
n
1 = 2, n
2 = 2, n
3 = 1, n
4 = 1, n = 6
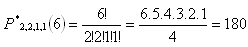
t = 180·5 Sek. = 900 Sek. = 15 Min.
Es gibt 180 mögliche Passwörter; das Testen aller würde 15 Minuten dauern.
10. Ein Student muss 4 Aufnahmeprüfungen ablegen. Für das Bestehen jeder Prüfung erhält er entweder 2, 3 oder 4 Punkte. Er muss mindestens 13 Punkte erreichen, um an die Universität zugelassen zu werden. Auf wie viele Arten kann er die Prüfungen bestehen, um erfolgreich zu sein?
Lösung:
Er muss 13, 14, 15 oder 16 Punkte erreichen.
| 13 Punkte: |
(3,3,3,4) |
P*3,1(4) = 4 |
| |
(4,4,3,2) |
P*2,1,1(4) = 12 |
| 14 Punkte: |
(4,4,4,2) |
P*3,1(4) = 4 |
| |
(4,4,3,3) |
P*2,2(4) = 6 |
| 15 Punkte: |
(4,4,4,3) |
P*3,1(4) = 4 |
| 16 Punkte: |
(4,4,4,4) |
P*4(4) = 1 |
N = 4 + 12 + 4 + 6 + 4 + 1 = 31
Es gibt 31 mögliche Arten, mindestens 13 Punkte zu erreichen.