Verformung von Festkörpern
1.Was sollten wir über die Verformung fester Körper wissen?
Lösung:
Verformung ist eine Veränderung der Form eines Körpers durch äußere Kräfte.
Verformung:
- a.) elastisch – reversibel, vorübergehend
- b.) plastisch – nicht elastisch, dauerhaft
Verformung kann durch Zug, Druck, Biegung, Scherung, Torsion oder eine Kombination verursacht werden.
Zugverformung:
Absolute Längenänderung:
Δl = l – l0
Relative Längenänderung:
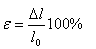
Normale Spannung:
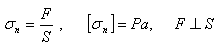
Hookesches Gesetz:
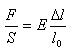
Das Hookesche Gesetz gilt nur bis zur Elastizitätsgrenze.
Spannungs-Dehnungs-Kurve:
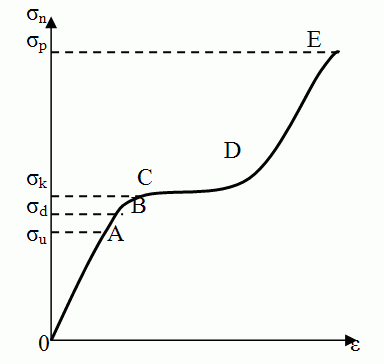
σu = Proportionalitätsgrenze
σd = σE = Elastizitätsgrenze (zulässige Spannung)
σk = Streckgrenze
σp = Zugfestigkeit
E = Elastizitätsmodul (Youngscher Modul) bei Zug
2.Bestimme, ob ein Eisendraht mit einem Durchmesser von 2 mm reißt, wenn er mit einer Kraft von 1 kN gespannt wird. (σE = 314 MPa)
Lösung:
Gegeben/Analyse:
d = 2 mm, r = 1 mm = 10-3 m, F = 103 N, σE = 314 MPa
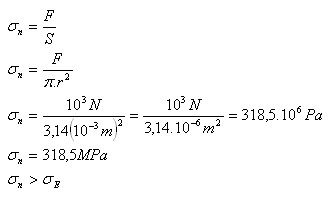
Da σn > σE, wird der Eisendraht reißen.
3.Berechne die relative Längenänderung eines Seils mit einer ursprünglichen Länge von 10 m, wenn es sich bei der Verformung um 40 mm verlängert.
Lösung:
Gegeben/Analyse:
l0 = 10 m, Δl = 40 mm = 0.04 m
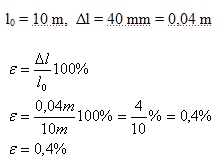
Die relative Längenänderung des Seils beträgt ε = 0,4%.
4.Wie ändert sich die normale Spannung in einem Draht, wenn die Zugkraft um das Vierfache zunimmt und der Drahtdurchmesser sich verdoppelt?
Lösung:
Gegeben/Analyse:
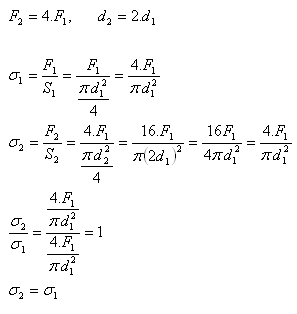
Die normale Spannung im Draht ändert sich nicht.
5.Wie groß muss der Radius eines Kupferdrahts (σp = 2·108 Pa) sein, damit er bei einer Kraft von 500 N nicht reißt?
Lösung:
Gegeben/Analyse:
F = 500 N, σp = 2·108 Pa
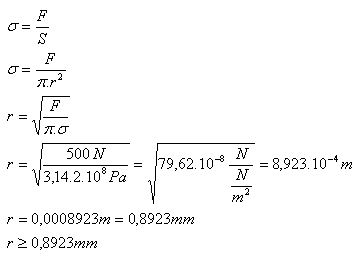
Der Draht muss einen Radius von mindestens r >= 0,89 mm haben.
6.Wie groß darf die maximale Länge eines vertikal aufgehängten Eisendrahts sein, damit er unter seinem Eigengewicht nicht reißt?
Lösung:
Gegeben/Analyse:
g = 9,81 m·s-2, ρ(Fe) = 7800 kg·m-3 = 7,8·103 kg·m-3, σp = 314·106 Pa
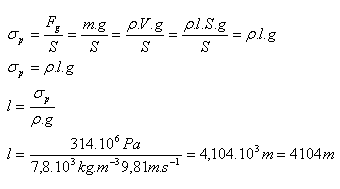
Die maximale Länge des Drahts beträgt 4104 m.
7.Welche Zugkraft wirkt in einer Gitarrensaite mit einer Länge von 0,65 m und einem Querschnitt von 0,325 mm2, wenn sie sich beim Spannen um 5 mm verlängert? (E = 220 GPa)
Lösung:
Gegeben/Analyse:
l0 = 0,65 m, Δl = 5·10-3 m, S = 0,325·10-6 m2, E = 220·109 Pa
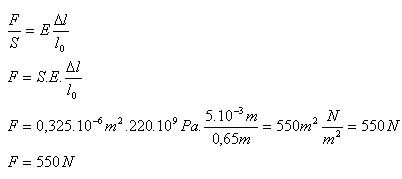
Die Gitarrensaite wird mit einer Kraft von F = 550 N gespannt.
8.Ein Aluminiumdraht mit einer ursprünglichen Länge von 4,2 m und einem Durchmesser von 1,1 mm verlängerte sich unter einer Kraft von 0,23 kN um 15,2 mm. Bestimme den Elastizitätsmodul E im Zug.
Lösung:
Gegeben/Analyse:
l0 = 4,2 m, r = 0,55·10-3 m, F = 0,23·103 N, Δl = 15,2·10-3 m

Der Elastizitätsmodul bei Zug für Aluminium beträgt E(Al) = 67 GPa.
9.Am Ende einer vertikalen Stahlstange (E = 220 GPa) mit einer Länge von 1,5 m soll eine Masse von 500 kg aufgehängt werden. Welchen Stangendurchmesser sollen wir wählen, wenn die Verlängerung nach dem Belasten höchstens 0,3 mm betragen darf? (Das Eigengewicht der Stange wird vernachlässigt.)
Lösung:
Gegeben/Analyse:
l0 = 1,5 m, m = 500 kg, Δl = 3·10-4 m, E = 220 GPa = 220·109 Pa, g = 10 m·s-2
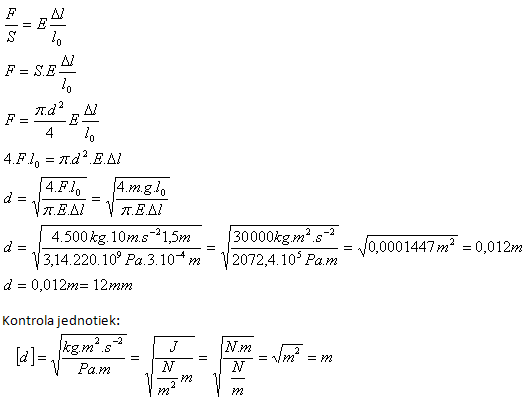
Wir wählen einen Stangendurchmesser von d = 12 mm.
10.Bestimme die Arbeit, die erforderlich ist, um eine Stahlstange (E = 220 GPa) mit einer Länge von 1 m und einem Querschnitt von 1 cm2 elastisch um 1 mm zu dehnen.
Lösung:
Gegeben/Analyse:
l0 = 1 m, Δl = 1 mm = 1·10-3 m, S = 1 cm2 = 1·10-4 m2, E = 220·109 Pa
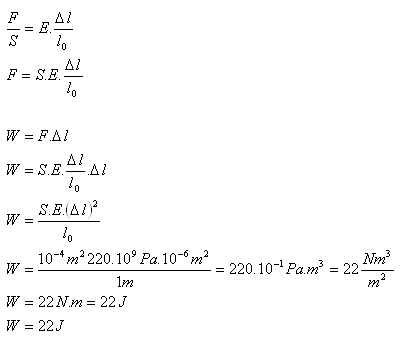
Um die Stahlstange zu dehnen, ist eine Arbeit von W = 22 J erforderlich.