Kombinationen
1. Charakterisieren Sie Kombinationen und Kombinationen mit Wiederholungen.
Lösung:
a)
k-Kombinationen aus einer Menge mit n Elementen (ohne Wiederholung)
k-Kombinationen aus einer Menge von n Elementen (ohne Wiederholung) sind eine ungeordnete Auswahl von k paarweise verschiedenen Elementen aus der gegebenen Menge.
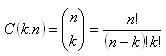
b)
k-Kombinationen aus einer Menge mit n Elementen (mit Wiederholung)
k-Kombinationen aus einer Menge von n Elementen (mit Wiederholung) sind eine ungeordnete Auswahl von k nicht unbedingt verschiedenen Elementen aus der gegebenen Menge.
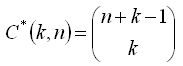
2. In der Ebene liegen 6 verschiedene Punkte (keine 3 liegen auf einer Geraden). Wie viele Strecken erhält man, wenn man alle Punkte miteinander verbindet?
Lösung:
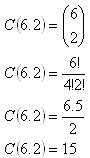
Man erhält 15 verschiedene Strecken.
3.Auf einem Kreis sind 9 Punkte markiert. Wie viele Dreiecke mit Eckpunkten in diesen Punkten gibt es?
Lösung:
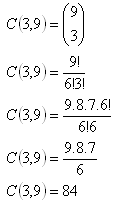
Es gibt 84 solcher Dreiecke.
4.a) Bestimmen Sie eine Formel zur Zählung der Diagonalen in einem konvexen n-Eck!
b) Wie viele Diagonalen hat ein Zehneck?
Lösung:
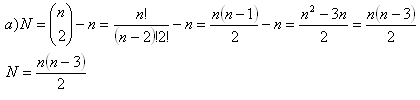
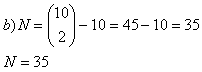
Ein konvexes Zehneck hat 35 Diagonalen.
5. Auf wie viele Arten kann man 8 von 32 Spielkarten auswählen, ohne die Reihenfolge zu beachten?
Lösung:
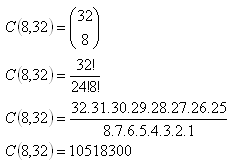
Die Spielkarten können auf 10 518 300 Arten ausgewählt werden.
6.Ein Lehrer hat 20 Aufgaben aus der Arithmetik und 30 aus der Geometrie vorbereitet. Für eine Klassenarbeit möchte er verwenden:
a) 3 Arithmetik- und 2 Geometrieaufgaben
b) 1 Arithmetik- und 2 Geometrieaufgaben
Auf wie viele Arten kann er die Arbeit zusammenstellen?
Lösung:
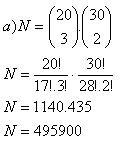
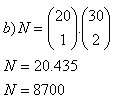
Der Lehrer kann entsprechend aus 495 900 bzw. 8 700 Arbeiten wählen.
7.Auf einer Abschlussfeier stießen die Absolventen mit ihren Gläsern an. Es gab 253 Anstoßgeräusche. Wie viele Absolventen kamen zur Feier?
Lösung:
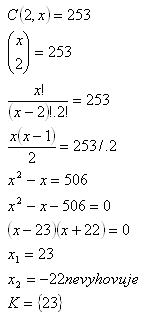
Auf der Feier waren 23 Absolventen.
8.Wenn die Anzahl der Elemente um 8 steigen würde, würde die Anzahl der Kombinationen mit k=2 ohne Wiederholung um das 11-Fache steigen. Wie viele Elemente gibt es?
Lösung:
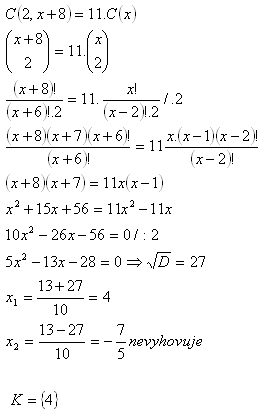
Es gibt 4 Elemente.
9. Für welche positive ganze Zahl x gilt:
Lösung:
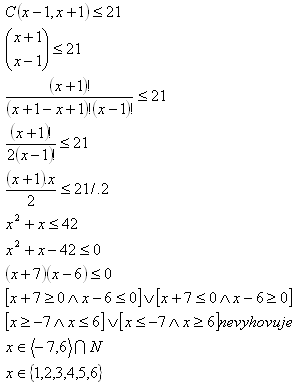
Die Ungleichung gilt für 1, 2, 3, 4, 5 und 6.
10.Zwei Gruppen bestehen zusammen aus 26 Elementen und ergeben zusammen 160 Kombinationen ohne Wiederholung für k=2. Wie viele Elemente sind in der ersten und wie viele in der zweiten Gruppe?
Lösung:
x – Anzahl der Elemente in der ersten Gruppe
y – Anzahl der Elemente in der zweiten Gruppe
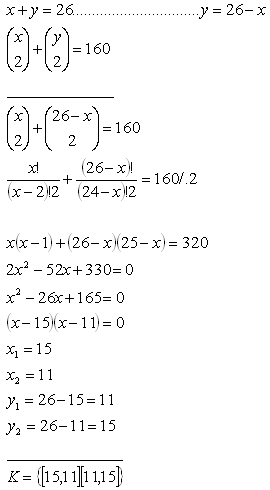
11. In der Konditorei werden 5 verschiedene Eissorten verkauft. Ein Vater möchte für seine Familie 15 Eiskugeln kaufen. Auf wie viele Arten kann er das Eis kaufen?
Lösung:
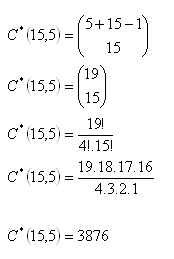
Der Vater kann das Eis auf 3876 verschiedene Arten kaufen.
12.Aus wie vielen Elementen können 15 Kombinationen mit Wiederholung (k=2) gebildet werden?
Lösung:
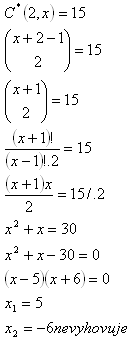
K = {5}
Die Kombinationen können aus 5 Elementen gebildet werden.