sk|cz|en|

Physik

Zustandsgleichung

1. Welche Beziehung besteht zwischen Druck, Volumen und Temperatur eines idealen Gases?

Lösung:

Der Zustand eines idealen Gases im thermodynamischen Gleichgewicht wird durch drei Zustandsgrößen beschrieben: Druck p, Volumen V und thermodynamische Temperatur T. Die wechselseitige Beziehung zwischen diesen Zustandsgrößen wird durch die Zustandsgleichung für ein ideales Gas ausgedrückt.

Zustandsgleichung für ein ideales Gas:

a) Für zwei Zustände (bei konstanter Gasmasse):

p1V1T1=p2V2T2\frac{p_1 V_1}{T_1} = \frac{p_2 V_2}{T_2}

b) Für ein Mol:

p⋅V=Rm⋅Tp \cdot V = R_m \cdot T Rm=8.314 J⋅K−1⋅mol−1R_m = 8.314 \, J \cdot K^{-1} \cdot mol^{-1}

c) Für n Mol:

p⋅V=n⋅Rm⋅Tp \cdot V = n \cdot R_m \cdot T

d) Für N Moleküle:

p⋅V=N⋅k⋅Tp \cdot V = N \cdot k \cdot T k=1.38⋅10−23 J⋅K−1k = 1.38 \cdot 10^{-23} \, J \cdot K^{-1}

e) Für m Kilogramm:

p⋅V=mMmRmTp \cdot V = \frac{m}{M_m} R_m T

f) Für ein Gemisch chemisch nicht reagierender Gase:

p⋅V=(m1Mm1+m2Mm2)RmTp \cdot V = \left(\frac{m_1}{M_{m1}} + \frac{m_2}{M_{m2}}\right) R_m T

 

2.Leiten Sie den Zahlenwert und die Dimension der molaren Gaskonstante Rm her.

Lösung:

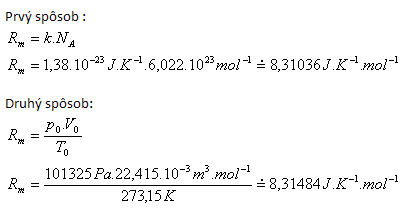
fyzika-stavova-rovnica-2.gif

Tabellierter Wert Rm = 3.31441 J·K-1·mol-1.

Abweichungen entstehen durch unterschiedliche Rundungen der Eingabewerte.

3.Ermitteln Sie, wie viele Moleküle in 1 cm3 eines beliebigen Gases unter Normalbedingungen enthalten sind.

Lösung:

Analyse:

V = 1 cm3 = 10-6 m3, p = 101325 Pa, T = 273.15 K

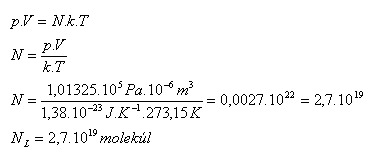
fyzika-stavova-rovnica-3.gif

Ein Kubikzentimeter eines beliebigen Gases unter Standardbedingungen enthält NL = 2,7·1019 Moleküle. Dies ist die Loschmidt-Zahl. (Johann Josef Loschmidt 1821–1895)

4. In einem Behälter mit Innenvolumen 8.3 m3 befindet sich Wasserstoff H2 mit der Masse 200 g und der Temperatur 27oC. Bestimmen Sie seinen Druck!

Lösung:

Analyse:

V = 8.3 m3, m = 200 g = 0.2 kg, t = 27oC, T = (27 + 273.15) K = 300.15 K
Mm = 2·10-3 kg·mol-1, Rm = 8.314 J·K-1·mol-1

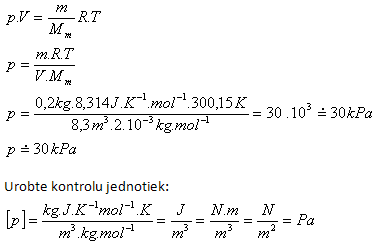
fyzika-stavova-rovnica-4.gif

Der Druck des Wasserstoffs im Behälter beträgt ungefähr 30 kPa.

5.In einem Behälter mit Innenvolumen 5·10-3 m3 befindet sich Stickstoff N2 bei der Temperatur 39oC und dem Druck 1.6·105 Pa. Bestimmen Sie seine Masse.

Lösung:

Analyse:

V = 5·10-3 m3, p = 1.6·105 Pa, T = 312.15 K, Rm = 8.314 J·K-1·mol-1
Mm = 2.14·10-3 kg·mol-1

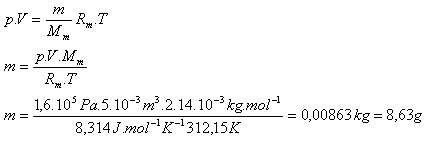
fyzika-stavova-rovnica-5.gif

Die Masse des Stickstoffs ist m = 8,63 g.

6.Wie groß ist der Luftdruck in einem Lkw-Reifen bei einer Temperatur von 20oC und einer Dichte von 8 kg·m-3. Mm(Luft) = 29·10-3 kg·mol-1

Lösung:

Analyse:

T = 293.15 K, ρ = 8 kg·m-3, Mm(Luft) = 29·10-3 kg·mol-1
Rm = 8.314 J·K-1·mol-1

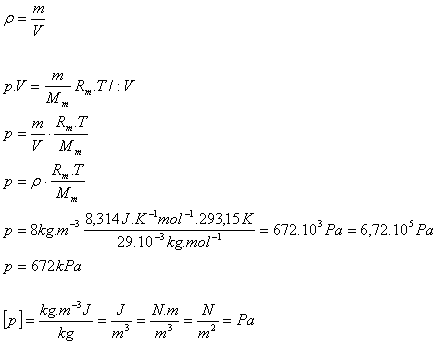
fyzika-stavova-rovnica-6.gif

Der Druck der Luft im Reifen beträgt p = 672 kPa.

7.Wie viele Moleküle befinden sich in einem kugelförmigen Behälter mit dem Innenradius 3 cm, der mit Sauerstoff O2 bei der Temperatur 27oC und dem Druck 1.36·10-2 Pa gefüllt ist?

Lösung:

Analyse:

r = 3 cm = 3·10-2 m, T = 300.15 K, p = 1.36·10-2 Pa
k = 1.38·10-23 J·K-1, V = 4/3·π·r3, N = ?

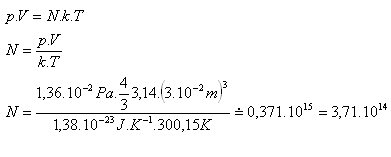
fyzika-stavova-rovnica-7.gif

Im Behälter befinden sich N = 3,71·1014 Moleküle Sauerstoff O2.

8.In einem Behälter befindet sich Stickstoff N2 mit der Masse 10 kg bei einem Druck von 10 MPa. Bestimmen Sie die Masse des Stickstoffs, die aus dem Behälter abgelassen werden muss, damit der Druck auf 2.5 MPa sinkt. (Die Temperatur des Stickstoffs ändert sich nicht)

Lösung:

Analyse:

m1 = 10 kg, p1 = 107 Pa, p2 = 2.5·106 Pa, T = konstant

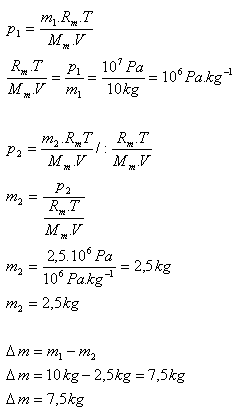
fyzika-stavova-rovnica-8.gif

Es müssen 7,5 kg Stickstoff aus dem Behälter abgelassen werden.

9.Die Dichte von Stickstoff unter Standardbedingungen (T1 = 273.15 K und p1 = 101325 Pa) beträgt ρ1 = 1.23 kg·m-3. Bestimmen Sie die Dichte von Stickstoff bei 30oC und Normaldruck.

Lösung:

Analyse:

T1 = 273.15 K, T2 = 303.15 K, p1 = p2 = 101325 Pa, ρ1 = 1.23 kg·m-3, ρ2 = ?

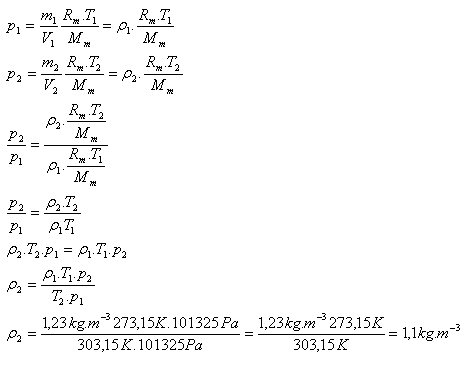
fyzika-stavova-rovnica-9.gif

Die Dichte von Stickstoff bei 30oC und Normaldruck beträgt 1,1 kg·m-3.

10. Berechnen Sie die effektive molare Masse der Luft Mm. Betrachten Sie Luft als ein Gemisch aus 75 % Stickstoff und 25 % Sauerstoff.

Lösung:

Analyse:

Mm(N2) = 28·10-3 kg·mol-1, m1(N2) = 0.75 m

Mm(O2) = 32·10-3 kg·mol-1, m2(O2) = 0.25 m

m = Gesamtmasse der Luft

Effektive molare Masse (gültig für zwei chemisch nicht reagierende Gase)

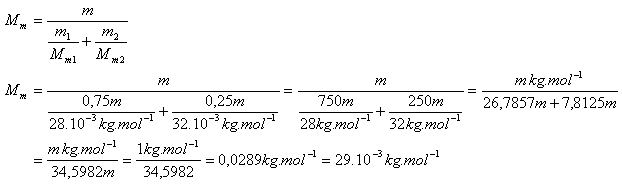
fyzika-stavova-rovnica-10.gif

Die effektive molare Masse der Luft beträgt Mm = 29·10-3 kg·mol-1.