Berechnung des Anteils und des prozentualen Anteils eines Elements in einer Verbindung
1.Ein Behälter enthält ein Gasgemisch mit 0,825 mol Schwefeldioxid, 4,29 mol Stickstoff, 0,055 mol Argon und 0,33 mol Sauerstoff. Berechne die Stoffmengenanteile der einzelnen Komponenten im System.
Lösung:
Zuerst berechnen wir die gesamte Stoffmenge im Gasgemisch:
n = (0,825 + 4,29 + 0,055 + 0,33) mol = 5,50 mol
Die Stoffmengenanteile der Komponenten werden wie folgt berechnet:
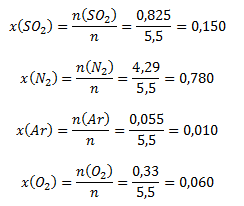
Die Stoffmengenanteile der Gase im Gemisch sind 0,15 (SO2); 0,78 (N2); 0,01 (Ar); 0,06 (O2).
2. Berechne:
- a) den Massenanteil und das Massenprozent von Schwefel und Eisen im Pyrit
- b) wie viele Gramm Schwefel in 500 g Pyrit enthalten sind
Lösung:
a) Der Massenanteil von Schwefel im Pyrit wird berechnet nach:
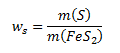
Wir formen diesen Ausdruck so um, dass er die Molmassen (aus Tabellen) und die Stoffmengen von Schwefel und Pyrit enthält. Wir drücken daher die Massen der gegebenen Stoffe aus als:
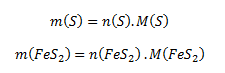
Nach dem Einsetzen dieser Beziehungen in die Gleichung für den Massenanteil erhalten wir:
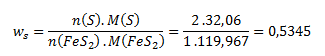
Der berechnete Massenanteil von Schwefel entspricht dem Massenprozent, gegeben durch:
Massenprozent = wS·100 = 0,5345 · 100 = 53,45 %
Der Massenanteil der zweiten Komponente des Pyrits, Eisen, ist dann:
wFe = 1 – 0,5345 = 0,4655
Massenprozent = 0,4655 · 100 = 46,55 %
3.Wieviel Prozent Stickstoff enthält Calciumdinitrat Ca(NO3)2?
Lösung:
Die Molmasse des Nitrats beträgt 164,086 g·mol-1. Die relative Atommasse des Stickstoffs ist 14,007. Logischerweise enthalten 164,086 Gramm der Verbindung 14,007 g Stickstoff. Zur Bestimmung des prozentualen Gehalts setzen wir die Masse des Stickstoffs ins Verhältnis zur Verbindung:
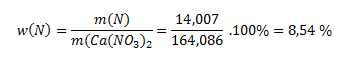
Stickstoff kommt in der Natur jedoch als Dimer N2 vor, daher ist der prozentuale Anteil von N2 doppelt so groß wie der von N; die korrekte Antwort ist 17,07 %.
4.25 cm3 Glycerin wurden in 100 cm3 Wasser gelöst. Berechne den Massenanteil von Glycerin in der Lösung und gib ihn in Massenprozent an. Die Dichte von Glycerin bei 20 °C beträgt 1,261 g·cm-3.
Lösung:
Die Masse des Glycerins wird berechnet aus:
m = ρ·V = 1,261 · 25 = 31,5 g
Die Masse der Lösung ist die Summe aus Glycerin und Wasser:
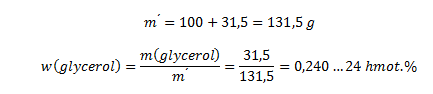
Die Lösung enthält 24 Massenprozent Glycerin.
5.Bei 25 °C und einem Druck von 101,5 kPa wurden 15,5 dm3 Wasserstoff H2 und 10 dm3 Neon Ne gemischt. Gib die Zusammensetzung des Gasgemischs an:
- a) in Volumenprozent
- b) in Molprozent
Lösung:
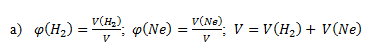
Nach dem Einsetzen der bekannten Werte erhalten wir:
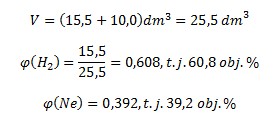
Das Gasgemisch enthält 60,8 Vol.% Wasserstoff und 39,2 Vol.% Neon.
b) Die Stoffmengen von Neon und Wasserstoff werden aus der Zustandsgleichung berechnet:
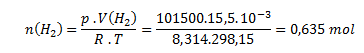
Neon wird analog berechnet:
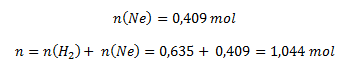
dann:
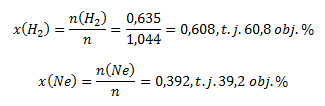
An den Lösungen in a) und b) sieht man, dass φi=xi. Dies gilt für Gase, deren Volumina unter denselben Zustandsbedingungen gemessen wurden.
6.Ein alkoholisches Getränk enthält 40 Vol-% Ethanol. Berechne die Volumina von reinem Ethanol und Wasser in 750 cm3 dieses Getränks.
Lösung:
Wir gehen von der Beziehung aus:
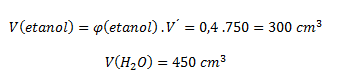
Das Getränk enthält 300 cm3 Ethanol und 450 cm3 Wasser.
7.Wie viele Gramm wasserfreies Kupfer(II)-sulfat sind in 12 g seines Pentahydrats mit einer Reinheit von 98,2 % enthalten?
Lösung:
Da das Verhältnis der Molmassen von wasserfreiem Salz und dessen Pentahydrat konstant ist, gilt für reine Stoffe der Masse m:
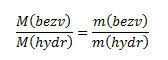
daraus die Masse des wasserfreien Kupfer(II)-sulfats:
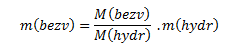
Da es sich in unserem Fall beim Hydrat nicht um einen reinen Stoff, sondern um ein Gemisch mit 98,2 % CuSO4·5H2O handelt, drücken wir m(hydr) aus mit:
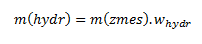
Einsetzen in die Beziehung ergibt:
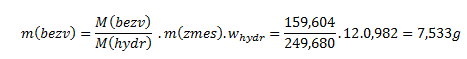
12 g Kupfervitriol mit der angegebenen Reinheit enthalten 7,533 g CuSO4.
8.Wieviel Prozent Schwefel enthält Schwefeltrioxid?
Lösung:
Die Molmasse von SO3 beträgt 80,062 g·mol-1, und die Molmasse von Schwefel 32,065 g·mol-1. Durch logisches Überlegen erhalten wir:
80,062 g Oxid entsprechen ..............100 %
32,065 g Schwefel entsprechen .................x %
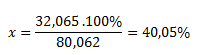
Schwefeltrioxid enthält 40,05 % Schwefel.
9.Welchen Prozentsatz seiner Masse verliert Grüner Vitriol FeSO4·7H2O beim Erhitzen auf hohe Temperatur (sodass er sein gesamtes Kristallwasser verliert)?
Lösung:
Die Molmasse von Eisen(II)-sulfat-Heptahydrat beträgt 278,05 g·mol-1, und die Molmasse des wasserfreien Sulfats 151,908. Nach dem Erhitzen des Heptahydrats bleibt reines wasserfreies Sulfat zurück, es gehen also sieben Mol Wasser verloren, das sind (7·18) g·mol-1 = 126 g·mol-1.
Logischerweise verlieren 278,05 Gramm des Heptahydrats 126 Gramm Wasser, was entspricht:
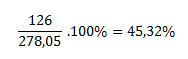
Das Glühen von Grünem Vitriol führt zu einem Verlust von 45,32 % der ursprünglichen Salzmasse.
10.Berechne die Masse einer gesättigten Lösung von Kaliumdichromat bei 50 °C, die aus 10 g reinem Dichromat hergestellt wurde. Bei 50 °C lösen sich 34,5 g K2Cr2O7 in 100 g Wasser.
Lösung:
Wir gehen von der umgestellten Formel für den Massenanteil aus:
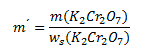
ws(K2Cr2O7) ist der Massenanteil von K2Cr2O7 in der gesättigten Lösung, berechnet aus der gegebenen Löslichkeit von K2Cr2O7:
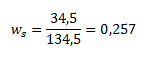
Wir setzen die ermittelten Werte ein:
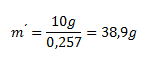
Aus 10 g K2Cr2O7 wurden 38,9 g einer bei 50 °C gesättigten K2Cr2O7-Lösung hergestellt.