Hydrostatik

1.Betrachten wir die grundlegenden Eigenschaften einer „idealen Flüssigkeit“.

Lösung:

Eine ideale Flüssigkeit ist ein Modell einer Flüssigkeit mit folgenden Eigenschaften:

a) hat keine Viskosität, sie ist vollkommen fließfähig
b) ist ein Kontinuum – die Teilchenstruktur wird nicht berücksichtigt
c) ist inkompressibel

Der Zustand einer Flüssigkeit an einem gegebenen Punkt wird durch den Druck p bestimmt:

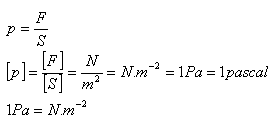
Durch eine äußere Kraft verursachter Druck – Pascalsches Gesetz:

Der durch eine äußere Kraft auf die Oberfläche einer Flüssigkeit ausgeübte Druck ist in allen Punkten der Flüssigkeit gleich.

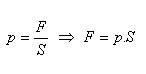
Durch das Gewicht der Flüssigkeit verursachter Druck – hydrostatischer Druck

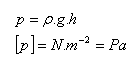
ρ – Dichte der Flüssigkeit, g = 10 m.s^-2, h – Tiefe, Abstand von der Oberfläche

Hydraulisches Prinzip:

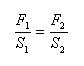
Archimedisches Prinzip:

Ein in eine Flüssigkeit eingetauchter Körper erfährt eine hydrostatische Auftriebskraft, die dem Gewicht der vom Körper verdrängten Flüssigkeit entspricht.

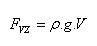
ρ – Dichte der Flüssigkeit,

V – Volumen des eingetauchten Teils des Körpers

Volumen der verdrängten Flüssigkeit

2.Ein Kolben mit Durchmesser d = 20 cm, der auf der Oberfläche einer Flüssigkeit liegt, wird mit einer Kraft F = 50 N belastet. Welchen Druck erzeugt diese Kraft in der Flüssigkeit?

Lösung:

Analyse:

d = 20 cm = 0.2 m, F = 50 N, p = ?

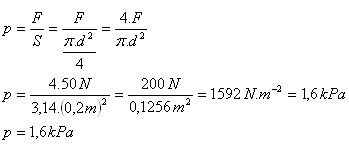
Die Kraft erzeugt in der Flüssigkeit einen Druck von etwa 1,6 kPa.

3.Berechnen Sie den Druck des Meerwassers (ρ = 1025 kg.m^-3) am Meeresboden

a.) in einer Tiefe von 3,6 km unter der Oberfläche
b.) am tiefsten ozeanischen Graben, dem Marianengraben im Pazifik (h = 11 034 m)

Lösung:

a.) p = ρ.g.h = 1025 kg.m^-3.10 m.s^-2.3600 m = 36 900 000 Pa = 36.9 MPa
b.) p = ρ.g.h = 1025 kg.m^-3.10 m.s^-2.11034 m = 113098500 Pa = 113.1 MPa

In 3,6 km Tiefe beträgt der Meerwasserdruck 36,9 MPa, am Grund des Marianengrabens 113,1 MPa.

4.Menschen sind ihr Leben lang an einen Luftdruck von etwa 1013 hPa gewöhnt. Bis zu welcher Tiefe können sie ohne Ausrüstung ins Meerwasser (ρ = 1025 kg.m^-3) tauchen?

Lösung:

Analyse:

p = 1013 hPa = 101 300 Pa, ρ = 1025 kg.m^-3

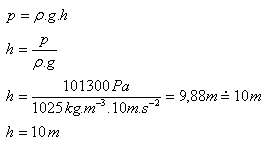
Ohne Ausrüstung können sie bis zu einer Tiefe von etwa 10 m tauchen.

5.In verbundene U-förmige Gefäße wurden Wasser (ρ₁ = 1000 kg.m^-3) und Quecksilber eingefüllt. Das Wasser erreichte in einem Schenkel die Höhe h₁ = 100 cm, das Quecksilber im anderen Schenkel h₂ = 7,35 cm. Bestimmen Sie die Dichte von Quecksilber ρ₂.

Lösung:

Analyse:

h₁ = 100 cm = 1 m, h₂ = 7.35 cm = 0.0735 m, ρ₁ = 1000 kg.m^-3

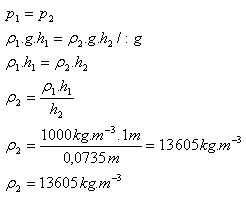
Quecksilber hat die Dichte ρ(Hg) = 13 605 kg.m^-3

6.In einem zylindrischen Gefäß mit Grundfläche S = 100 cm² befinden sich 2 kg Quecksilber (ρ₁ = 13 600 kg.m^-3) und 1 kg Wasser (ρ₂ = 1000 kg.m^-3). Bestimmen Sie den hydrostatischen Druck am Boden!

Lösung:

Analyse:

S = 100 cm² = 0.01 m², m₁ = 2 kg, m₂ = 1 kg, ρ₁ = 13 600 kg.m^-3, ρ₂ = 1000 kg.m^-3

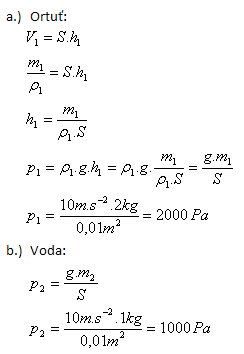
p = p₁ + p₂

p = 2000 Pa + 1000 Pa = 3000 Pa

Der gesamte hydrostatische Druck am Boden beträgt p = 3000 Pa

7.Berechnen Sie die Druckkraft auf den Deckel eines Glases mit Durchmesser 8 cm, wenn der Innendampfdruck 2,5 kPa und der atmosphärische Druck 101325 Pa beträgt. (Nehmen Sie an, dass die Luft im Inneren des Glases vollständig evakuiert ist.)

Lösung:

Analyse:

p₁ = 2.5 kPa = 0.025·10⁵ Pa, p₂ = 1.01325·10⁵ Pa, d = 8 cm = 0.08 m, r = 0.04 m

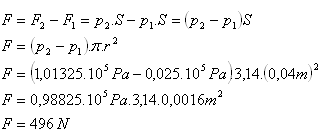
Die Druckkraft auf den Deckel beträgt F = 496 N.

8.Ein Tourist maß den Luftdruck am Fuß eines Berges: 1020 hPa, und am Gipfel: 955 hPa. Welche Höhendifferenz überwand der Tourist beim Aufstieg? (ρ_Luft = 1,3 kg.m^-3)

Lösung:

Analyse:

p₁ = 1020 hPa = 102000 Pa, p₂ = 955 hPa = 95500 Pa, ρ_Luft = 1.3 kg.m^-3

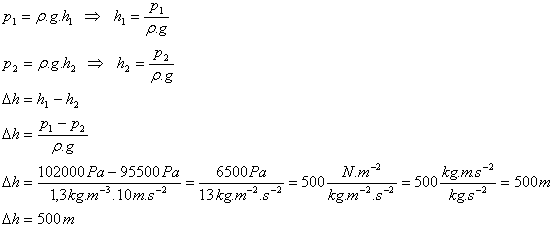
Der Tourist überwand eine Höhendifferenz von 500 m.

9.Eine kleine Hydraulikpresse hat einen Kolbendurchmesser von 1,4 m, der Pumpenkolben einen Durchmesser von 8 cm. Welche Kraft wirkt auf den Pressenkolben, wenn auf den Pumpenkolben eine Kraft von 4 N ausgeübt wird?

Lösung:

Analyse:

d₁ = 1.4 m, d₂ = 8 cm = 0.08 m, F₂ = 4 N, F₁ = ?

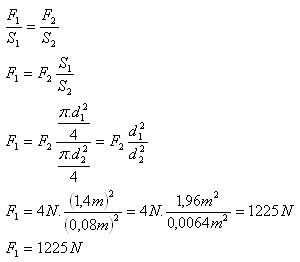
Auf den Pressenkolben wirkt eine Kraft F₁ = 1225 N.

10.Der Radius der kreisförmigen Grundfläche des kleineren Kolbens einer Hydraulikpresse beträgt 4 cm. Welchen Radius muss der größere Kolben haben, wenn mit einer Kraft von 80 N eine Druckkraft von 11 520 N erzeugt werden soll?

Lösung:

Analyse:

F₁ = 80 N, F₂ = 11 520 N, r₁ = 4 cm = 0.04 m, r₂ = ?

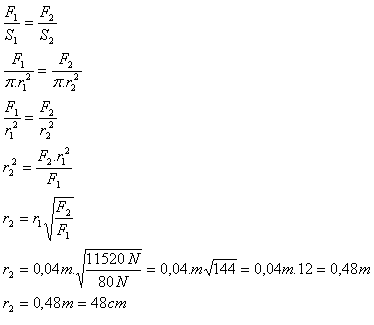
Der Radius des größeren Kolbens beträgt 48 cm.

11.Die Norm verlangt, dass in einem U-Boot durchschnittlich 20 m³ Raum pro Matrose vorhanden sein müssen. Wie viele Matrosen können in einem U-Boot arbeiten, wenn beim Eintauchen in Meerwasser (ρ = 1020 kg.m^-3) die Auftriebskraft auf das U-Boot 15,3 MN beträgt?

Lösung:

Analyse:

ρ = 1020 kg.m^-3, V’ = 20 m³, F_B= 15.3 MN = 15 300 000 N

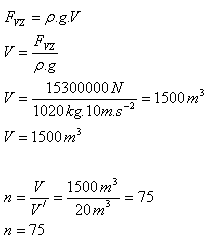
Das U-Boot kann 75 Matrosen aufnehmen.

12.Ein Aräometer hat ein Volumen von 150 cm³. Wie tief wird es in eine Flüssigkeit mit der Dichte ρ = 850 kg.m^-3 eintauchen?

Lösung:

Analyse:

V = 150 cm³ = 0.00015 m³, ρ = 850 kg.m^-3

Das Aräometer taucht bis zu einer Tiefe von 12,0 cm ein.

13.Wie viel Kerosin (ρ = 800 kg.m^-3) muss in ein Fass mit einem Volumen von 200 Litern gefüllt werden, damit es vollständig untergetaucht im Wasser schwimmt?

Lösung:

Analyse:

V = 200 l = 0.2 m³, ρ_ker = 800 kg.m^-3, ρ_w = 1000 kg.m^-3

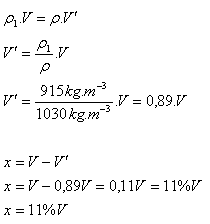
Das Fass muss mit 160 kg Kerosin gefüllt werden.

14.Kann ein Holzblock mit der Dichte ρ = 850 kg.m^-3 auf den Grund eines Flusses sinken, wenn eine Eisenkette mit der Masse 1,5 kg daran befestigt ist? Das Volumen des Blocks beträgt 0.01 m³.

Lösung:

Analyse:

ρ_wood = 850 kg.m^-3, V = 0.01 m³, m_chain = 1.5 kg, ρ_w = 1000 kg.m^-3

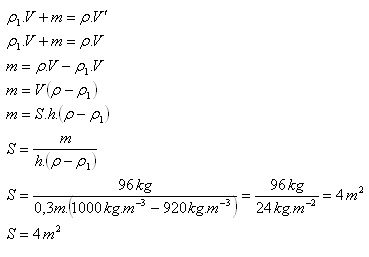
Der Block mit der Kette sinkt nicht – er schwimmt.

15.Ein Körper mit der Masse 800 g und dem Volumen 1,2 dm³ schwimmt auf der Wasseroberfläche. Welcher Anteil seines Volumens ragt über die Wasseroberfläche heraus?

Lösung:

Analyse:

m = 0.8 kg, V = 1.2 dm³ = 0.0012 m³, ρ_w = 1000 kg.m^-3

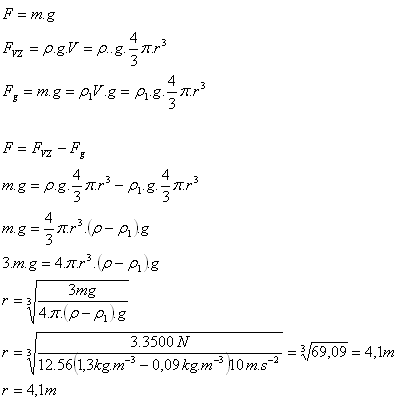
33 % des Volumens ragen über die Wasseroberfläche hinaus.

16.Das Volumen einer Hohlkugel beträgt 8 Liter, die Masse 4,5 kg. Wird die Kugel im Wasser schwimmen?

Lösung:

Analyse:

V = 8 l = 0.008 m³, m = 4.5 kg, ρ_w = 1000 kg.m^-3

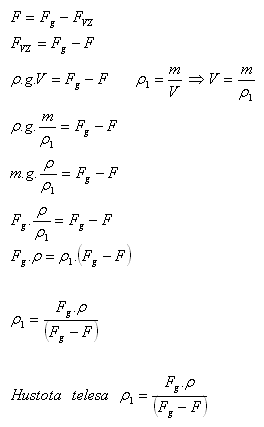
Die Kugel schwimmt auf dem Wasser.

17.Welcher Bruchteil seines Volumens ist in Kerosin (ρ = 800 kg.m^-3) eingetaucht, wenn die Dichte des Körpers ρ = 600 kg.m^-3 beträgt?

Lösung:

Analyse:

ρ_body = 600 kg.m^-3, ρ_ker = 800 kg.m^-3

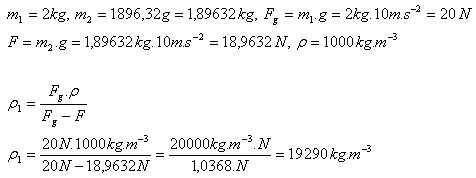
Der Körper ist zu 75 % seines Volumens eingetaucht.

18.

Wie groß ist die Druckkraft des Wassers auf den Boden eines Beckens mit den Abmessungen 20 m × 12 m und einer Tiefe von 1,8 m?

Lösung:

Analyse:

a = 20 m, b = 12 m, h = 1.8 m, ρ_w = 1000 kg.m^-3

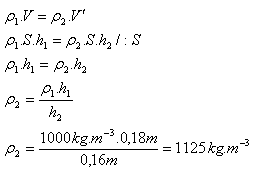
Die Druckkraft beträgt F = 4,2 MN.

19.Ein quaderförmiger Körper mit der Dichte ρ = 600 kg.m^-3 und dem Volumen V = 0.01 m³ schwimmt auf Wasser. Welche Kraft ist nötig, um ihn vollständig unter die Wasseroberfläche zu drücken?

Lösung:

Analyse:

ρ_body = 600 kg.m^-3, V = 0.01 m³, ρ_w = 1000 kg.m^-3

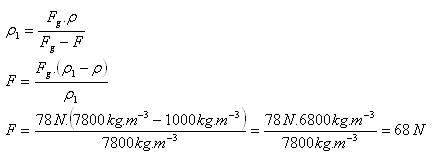
Die benötigte Kraft beträgt F = 39 N.

20.Ein Block mit Volumen V = 1,2 dm³ schwimmt im Wasser, wobei 1/4 seines Volumens herausragt. Wie groß ist seine Dichte?

Lösung:

Analyse:

V = 1.2 dm³ = 0.0012 m³, V_out = 1/4 V, ρ_w = 1000 kg.m^-3

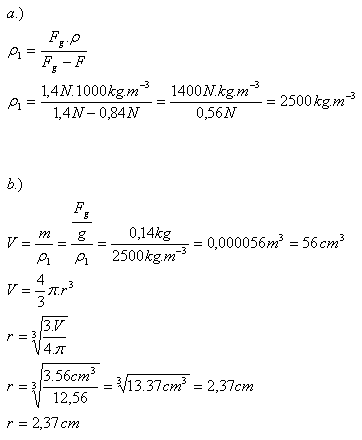
Die Dichte des Blocks beträgt ρ = 750 kg.m^-3

21.Ein Floß mit der Masse m = 500 kg und dem Volumen V = 2 m³ schwimmt auf dem Wasser. Wie viele Personen mit einer Masse von 75 kg kann es tragen, wenn mindestens 1/10 seines Volumens über der Wasseroberfläche bleiben muss?

Lösung:

Analyse:

m = 500 kg, V = 2 m³, ρ_w = 1000 kg.m^-3, m_p = 75 kg

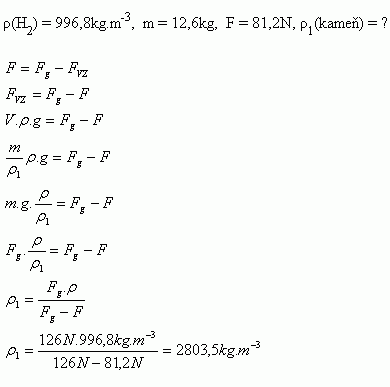
Das Floß kann 20 Personen tragen.

Physik

Hydrostatik

Adblock detected