Hydrostatics
1.Let’s review the basic properties of an “ideal liquid.”
Solution:
An ideal liquid is a model of a liquid with the following properties:
- a) has no viscosity, it is perfectly fluid
- b) is a continuum – we do not consider its particle structure
- c) it is incompressible
The state of a liquid at a given point is determined by pressure p:
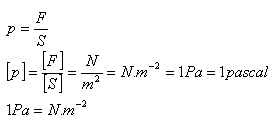
Pressure caused by an external force – Pascal’s law:
The pressure exerted by an external force acting on the surface of a liquid is the same at all points of the liquid.
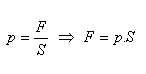
Pressure caused by the weight of the liquid – hydrostatic pressure
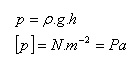
ρ – density of the liquid, g = 10 m.s-2, h – depth, distance from the surface
Hydraulic principle:
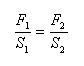
Archimedes’ principle:
A body immersed in a liquid is buoyed up by a hydrostatic buoyant force equal to the weight of the liquid displaced by the body.
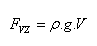
ρ – density of the liquid,
V – volume of the submerged part of the body
volume of displaced liquid
2.A piston with a diameter d = 20 cm lying on the surface of a liquid is subjected to a force F = 50 N. What pressure does this force create in the liquid?
Solution:
Analysis:
d = 20 cm = 0.2 m, F = 50 N, p = ?
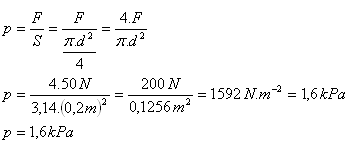
The force creates a pressure of about 1.6 kPa in the liquid.
3.Calculate the pressure of seawater (ρ = 1025 kg.m-3) at the sea bottom
- a.) at a depth of 3.6 km below the surface
- b.) at the deepest ocean trench, the Mariana Trench in the Pacific Ocean (h = 11 034 m)
Solution:
- a.) p = ρ.g.h = 1025 kg.m-3.10 m.s-2.3600 m = 36 900 000 Pa = 36.9 MPa
- b.) p = ρ.g.h = 1025 kg.m-3.10 m.s-2.11034 m = 113098500 Pa = 113.1 MPa
At a depth of 3.6 km the seawater pressure is 36.9 MPa, at the bottom of the Mariana Trench the pressure is 113.1 MPa.
4.People are used to air pressure of about 1013 hPa throughout their lives. To what depth can they dive into seawater (ρ = 1025 kg.m-3) without equipment?
Solution:
Analysis:
p = 1013 hPa = 101 300 Pa, ρ = 1025 kg.m-3
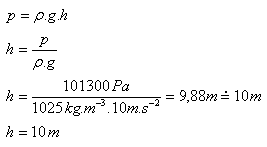
Without equipment, they can dive to a depth of about 10 m.
5.Into connected U-shaped vessels water (ρ1 = 1000 kg.m-3) and mercury were poured. The water in one arm reached a height of h1 = 100 cm, mercury in the other arm to h2 = 7.35 cm. Determine the density of mercury ρ2.
Solution:
Analysis:
h1 = 100 cm = 1 m, h2 = 7.35 cm = 0.0735 m, ρ1 = 1000 kg.m-3
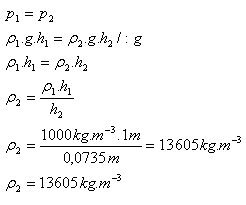
Mercury has density ρ(Hg) = 13 605 kg.m-3
6.In a cylindrical container with base S = 100 cm2 there are 2 kg of mercury (ρ1 = 13 600 kg.m-3) and 1 kg of water (ρ2 = 1000 kg.m-3). Determine the hydrostatic pressure at the bottom!
Solution:
Analysis:
S = 100 cm2 = 0.01 m2, m1 = 2 kg, m2 = 1 kg, ρ1 = 13 600 kg.m-3, ρ2 = 1000 kg.m-3
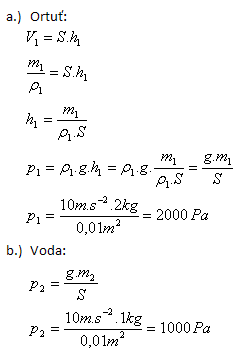
p = p1 + p2
p = 2000 Pa + 1000 Pa = 3000 Pa
Total hydrostatic pressure at the bottom is p = 3000 Pa
7.Calculate the pressure force acting on the lid of a jar with diameter 8 cm, if the internal steam pressure is 2.5 kPa and the atmospheric pressure is 101325 Pa. (Assume the air inside the jar is completely evacuated.)
Solution:
Analysis:
p1 = 2.5 kPa = 0.025·105 Pa, p2 = 1.01325·105 Pa, d = 8 cm = 0.08 m, r = 0.04 m
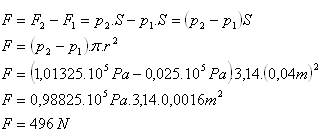
The pressure force on the lid is F = 496 N.
8.A tourist measured atmospheric pressure at the foot of a mountain: 1020 hPa, and at the top: 955 hPa. What altitude difference did the tourist overcome while climbing? (ρair = 1.3 kg.m-3)
Solution:
Analysis:
p1 = 1020 hPa = 102000 Pa, p2 = 955 hPa = 95500 Pa, ρair = 1.3 kg.m-3
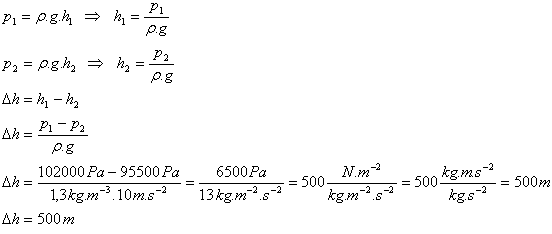
The tourist overcame an altitude difference of 500 m.
9.A small hydraulic press has a piston diameter of 1.4 m, the pump piston diameter is 8 cm. What force acts on the press piston if the pump piston is subjected to a force of 4 N?
Solution:
Analysis:
d1 = 1.4 m, d2 = 8 cm = 0.08 m, F2 = 4 N, F1 = ?
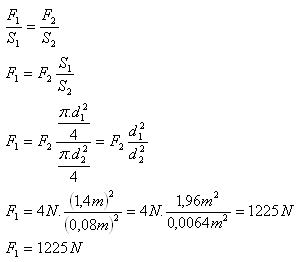
The press piston is subjected to a force F1 = 1225 N.
10.The radius of the circular base of the smaller piston of a hydraulic press is 4 cm. What radius must the larger piston have if a force of 80 N should generate a pressure force of 11 520 N?
Solution:
Analysis:
F1 = 80 N, F2 = 11 520 N, r1 = 4 cm = 0.04 m, r2 = ?
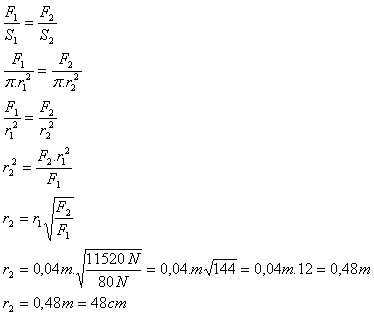
The radius of the larger piston is 48 cm.
11.The standard requires that in a submarine there must be on average 20 m3 of space per sailor. How many sailors can work in a submarine if, when submerged in seawater (ρ = 1020 kg.m-3), the buoyant force on the submarine is 15.3 MN?
Solution:
Analysis:
ρ = 1020 kg.m-3, V’ = 20 m3, FB = 15.3 MN = 15 300 000 N
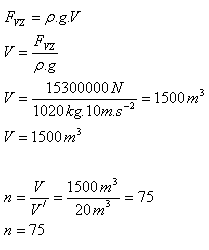
The submarine can accommodate 75 sailors.
12.A hydrometer has a volume of 150 cm3. How deep will it sink into a liquid of density ρ = 850 kg.m-3?
Solution:
Analysis:
V = 150 cm3 = 0.00015 m3, ρ = 850 kg.m-3

The hydrometer sinks to a depth of 12.0 cm.
13.How much kerosene (ρ = 800 kg.m-3) must be poured into a barrel with a volume of 200 liters so that it would float completely submerged in water?
Solution:
Analysis:
V = 200 l = 0.2 m3, ρker = 800 kg.m-3, ρw = 1000 kg.m-3
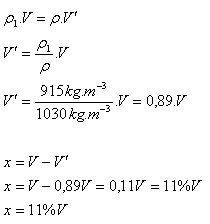
The barrel must be filled with 160 kg of kerosene.
14.Can a wooden block of density ρ = 850 kg.m-3 sink to the bottom of a river if an iron chain of mass 1.5 kg is tied to it? The volume of the block is 0.01 m3.
Solution:
Analysis:
ρwood = 850 kg.m-3, V = 0.01 m3, mchain = 1.5 kg, ρw = 1000 kg.m-3
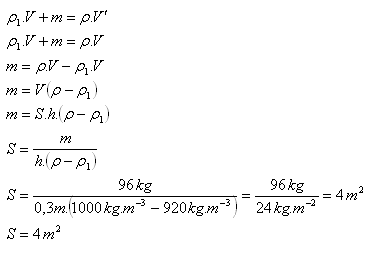
The block with the chain does not sink – it floats.
15.A body of mass 800 g and volume 1.2 dm3 floats on the surface of water. What part of its volume sticks out above the water surface?
Solution:
Analysis:
m = 0.8 kg, V = 1.2 dm3 = 0.0012 m3, ρw = 1000 kg.m-3
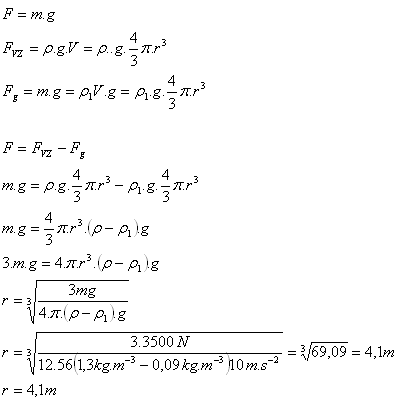
Above the water surface sticks out 33% of the body’s volume.
16.The volume of a hollow sphere is 8 liters, the mass is 4.5 kg. Will the sphere float in water?
Solution:
Analysis:
V = 8 l = 0.008 m3, m = 4.5 kg, ρw = 1000 kg.m-3
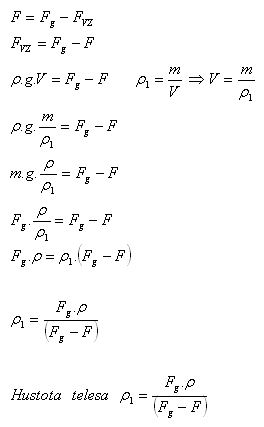
The sphere floats on water.
17.What fraction of its volume is submerged in kerosene (ρ = 800 kg.m-3) if the body’s density is ρ = 600 kg.m-3?
Solution:
Analysis:
ρbody = 600 kg.m-3, ρker = 800 kg.m-3
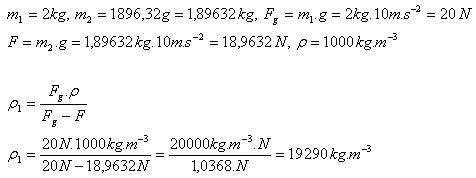
The body is submerged with 75% of its volume.
18.
What is the pressure force of water on the bottom of a pool with dimensions 20 m × 12 m and depth 1.8 m?
Solution:
Analysis:
a = 20 m, b = 12 m, h = 1.8 m, ρw = 1000 kg.m-3

The pressure force is F = 4.2 MN.
19.A cuboid-shaped body of density ρ = 600 kg.m-3 and volume V = 0.01 m3 floats on water. What force is needed to immerse it completely below the water surface?
Solution:
Analysis:
ρbody = 600 kg.m-3, V = 0.01 m3, ρw = 1000 kg.m-3

The force needed is F = 39 N.
20.A block of volume V = 1.2 dm3 floats in water with 1/4 of its volume sticking out. What is its density?
Solution:
Analysis:
V = 1.2 dm3 = 0.0012 m3, Vout = 1/4 V, ρw = 1000 kg.m-3

The density of the block is ρ = 750 kg.m-3
21.A raft of mass m = 500 kg and volume V = 2 m3 floats on water. How many people of mass 75 kg can it carry, if at least 1/10 of its volume must remain above the water surface?
Solution:
Analysis:
m = 500 kg, V = 2 m3, ρw = 1000 kg.m-3, mp = 75 kg

The raft can carry 20 people.