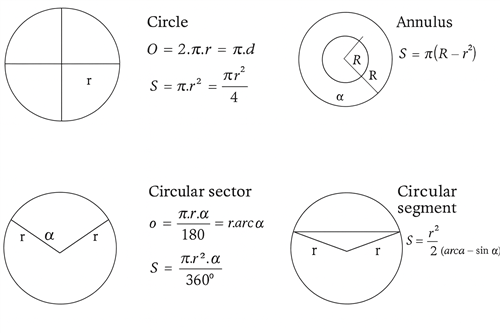
Circle

1. Characterize the circle and its parts:

Solution:

2. The distance between the centers of two externally tangent circles is 12 cm, and the sum of the areas of both circles is 80π cm².

Solution:



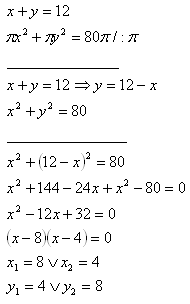
The radii of the circles are r₁ = 8 cm, r₂ = 4 cm.

3. Divide a circle with radius R = 28 cm by a concentric circle so that the areas of the resulting parts are equal.

Solution:



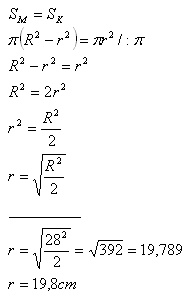
The radius of the smaller concentric circle is r = 19.8 cm.

4. Calculate the radius of a circle if its chord length is t = 16 cm and the height of the corresponding circular segment is v = 5 cm.

Solution:



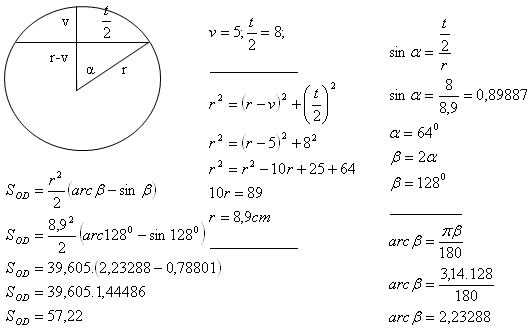
The radius of the circle is r = 8.9 cm.
The area of the circular segment is S_OD = 57.22 cm².

5. A circle with radius R is divided by a concentric circle with radius r. The ratio of the area of the inner circle to the area of the annulus is the same as the ratio of the area of the annulus to the area of the outer circle.

Solution:

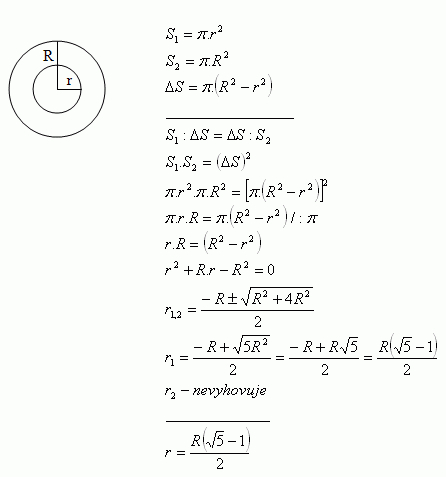
6. Three identical circles (r = 8 cm) touch each other.

Solution:



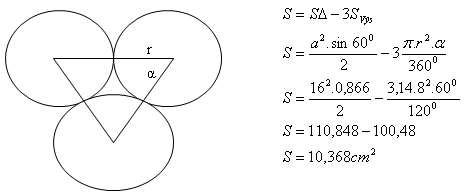
The area of the region is S = 10.368 cm².

7. An isosceles triangle has a = 10 cm, b = c = 13 cm. A circle is inscribed in the triangle.

Solution:



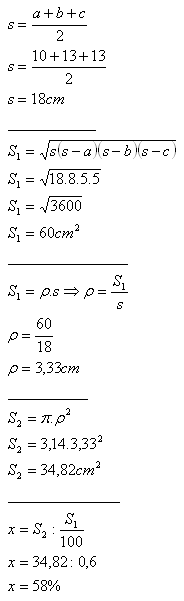
The circle occupies 58% of the triangle's area.

8. The height of the circular segment is 2 cm, and the central angle α = 60°.

Solution:


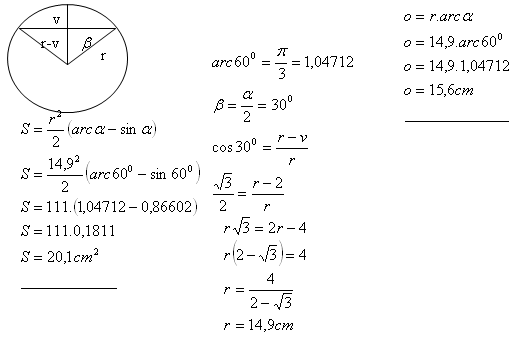
The area of the circular segment is S = 20.1 cm², and the arc length is o = 15.6 cm.

9. There is a path 40 cm wide around a circular flowerbed. The flowerbed has a diameter of 3 m 20 cm.

Solution:



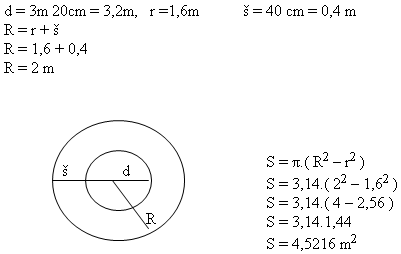
The area of the path around the flowerbed is S = 4.5216 m².

10. The first gear of a gear train has 60 teeth. The second gear meshing with the first has 42 teeth. The third gear meshing with the second has 15 teeth. The first gear rotates seven times.

Solution:



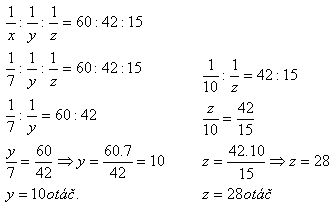
The third gear rotates 28 times.