Derivative of an undeveloped function
1. How do we differentiate an implicit function?
Solution:
Let an implicit function F[x; f(x)] = 0 be given. When differentiating it, differentiate the terms containing only x in the usual way; differentiate the terms with y as composite functions. Multiply their derivative (with respect to y) by y′. Solve the equation for y′.
For example:
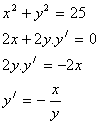
2. Differentiate the function:
Solution:
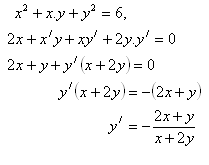
3. Differentiate the function:
Solution:
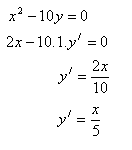
4.Differentiate the function:
Solution:
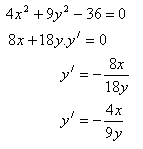
5.Under what angle do the curves x2 + y2 – 5 = 0 and y2 – 4x = 0 intersect?
Solution:
The angle of intersecting curves equals the angle of their tangents at the common point T. Common point T:
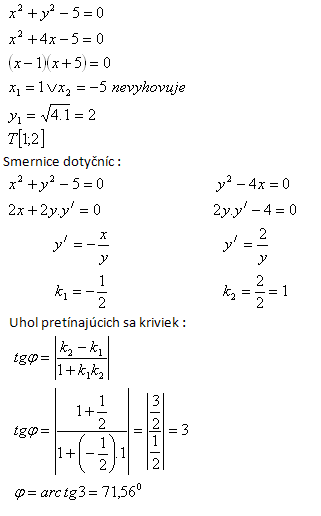
6.Differentiate the function x3 + y3 − 3axy = 0
Solution:
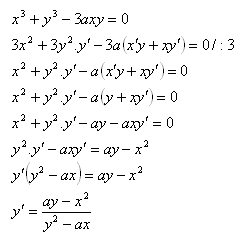
7.Differentiate the function ey + e–x + xy = 0
Solution:
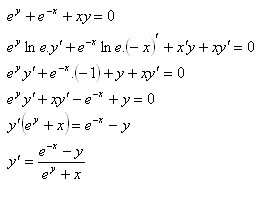
8.Compute the first derivative of the function exy − x2 + y3 = 0 at x = 0
Solution:
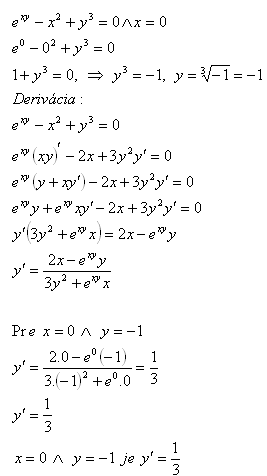
9.Write the equation of the tangent to the circle x2 + y2 + 4x − 4y + 3 = 0 at the point where the circle intersects the x-axis.
Solution:
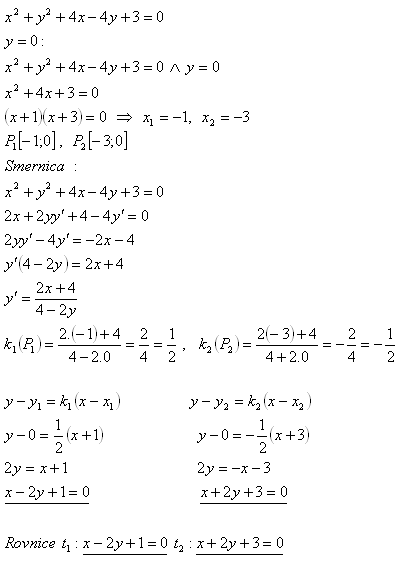
10.Write the equation of the tangent to the curve
Solution:
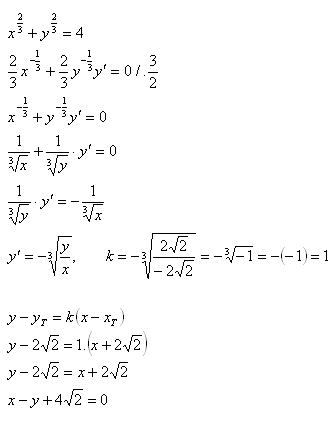
The equation of the tangent is x − y + 4√2 = 0