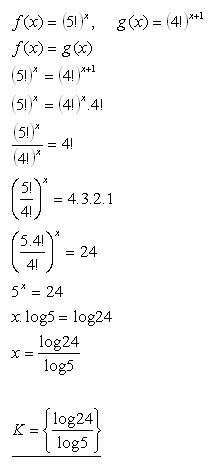Function features
1. What do you remember about the properties of functions?
Solution:
A function f of a real variable x is a rule that assigns to each x ∈ R at most one y ∈ R such that
y = f(x)
The domain of the function D is the set of all x ∈ R for which there exists exactly one y ∈ R such that
y = f(x).
The range of the function H is the set of all y ∈ R for which there exists at least one x ∈ R such that
y = f(x).

Two functions are equal: f(x) = g(x) if: D(f) = D(g)
f(x) = g(x)
Which of the following graphs represent functions?
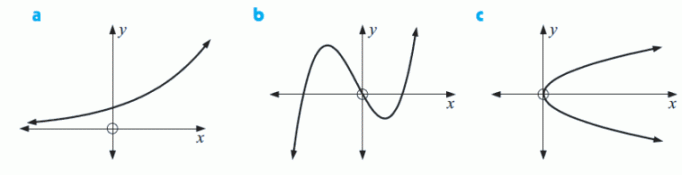
Function Function Not a function
2.Determine whether the following expressions are functions:
Solution:
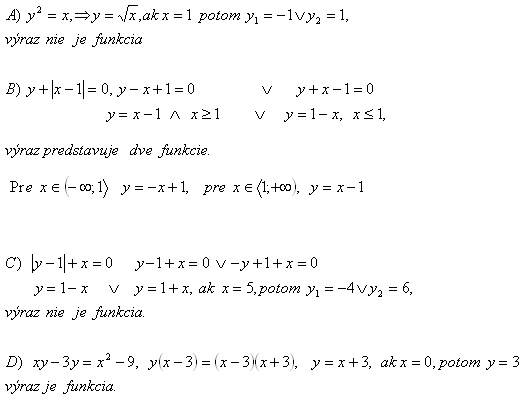
3.Decide whether the following functions are equal:
Solution:
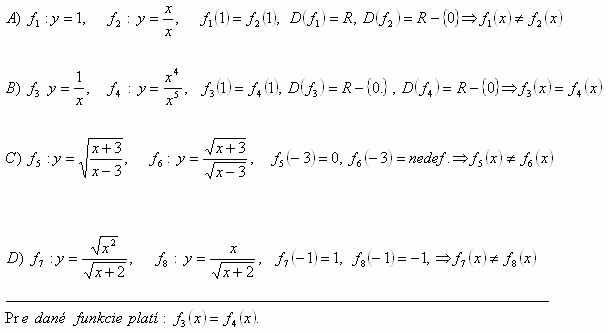
4.Determine the evenness or oddness of the functions:
Solution:
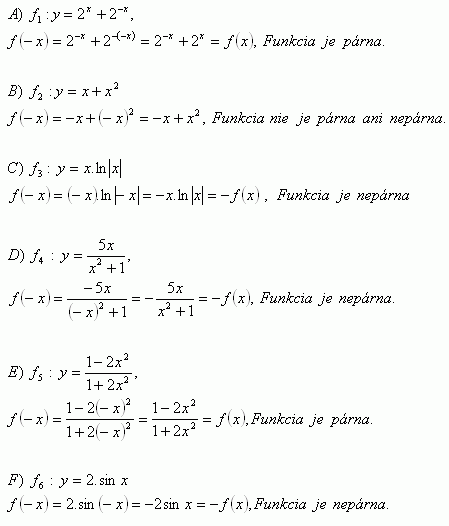
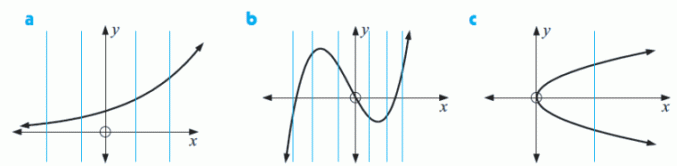
5. Determine which of the following functions are bounded in the given domain.
Solution:

6. For the given functions, create inverse functions.
Solution:
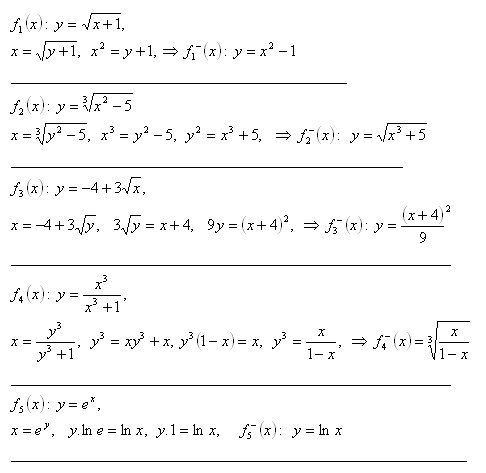
7. Determine the inverse function for the functions:
Solution:
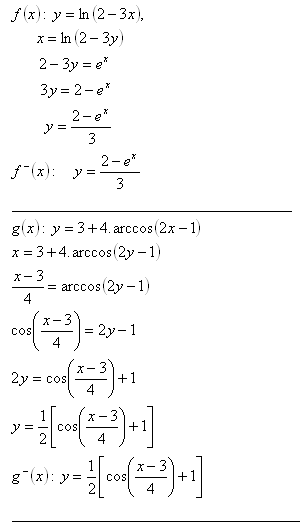
8. In the function f(x): y = ax2 + bx + c , x ∈ R, determine a, b, c ∈ R such that f(0) = -3, f(-1) = -6, f(2) = 15.
Solution:
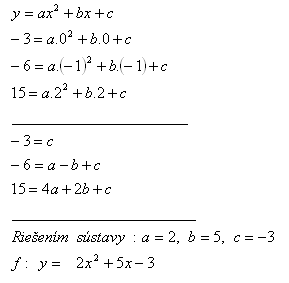
9. Determine b, d of the function f: y = (x + b):(x + d) such that f(1) = -1, f(-1) = -1/3
Solution:
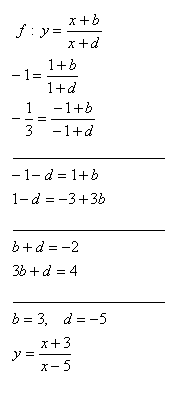
10.Determine the set of all functions f(x) for which the following holds:
Solution:

11.The function f: y= -2x +3 is given
a.) Determine f(0), f(-5)
b.) For which x is f(x) = 1, f(x) = -5
c.) Determine the intersection of the graph of the function with the coordinate axes
Solution:
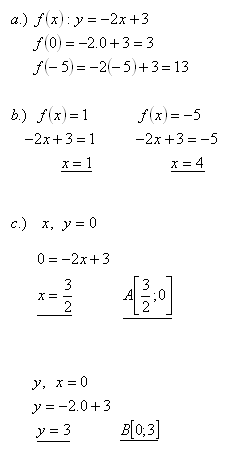
12.Write a linear function whose graph passes through the points
Solution:
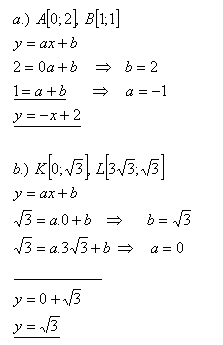
The equations of the functions are: f1: y = – x + 2 and f2: y = √3.
13.According to the car manufacturer, the fuel consumption of a car per 100 km is as follows. At a speed of 80 km/h it consumes 6 liters of fuel, at a speed of 110 km/h it consumes 8.1 liters. Determine the car’s consumption at a speed of 90 km/h.
Solution:
x = speed, y = consumption
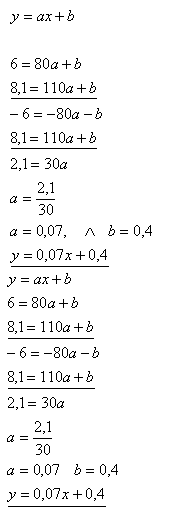
Consumption at a speed of 90 km/h.
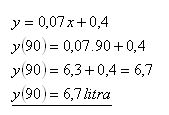
The fuel consumption of the car at a speed of 90 km/h is 6.7 liters per 100 kilometers.
14.The function f: y = x2 - 4x -12 is given.
a.) Determine for which x it holds that f(x) = 9
b.) Determine the intersections of the graph of the function with the coordinate axes
Solution:
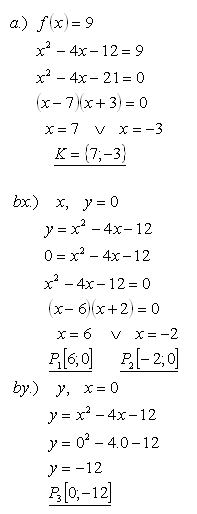
15.Write a quadratic function whose elements are the ordered pairs
A[0;1], B[2;-1], C[1;-1]
Solution:
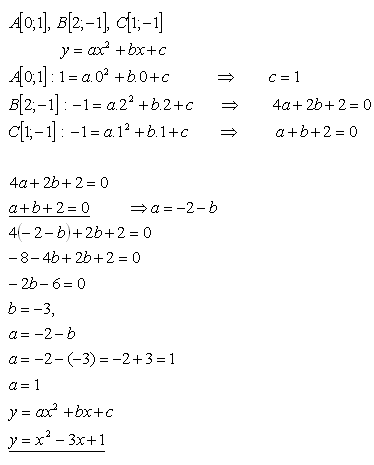
The quadratic function has the equation: f : y = x2 - 3x +1
16.The quadratic function f: y = x2 – 3x + c is given. Determine c such that the function
a.) has no common point with the x-axis
b.) has exactly one common point with the x-axis
c.) has exactly two common points with the x-axis
Solution:
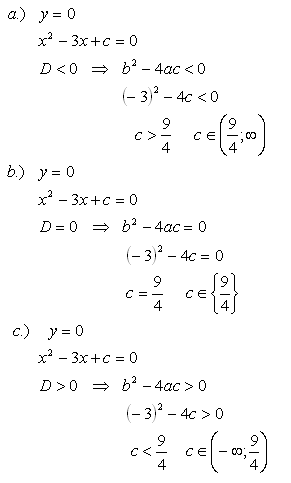
17.The quadratic function f: y = x2 + 4x – 5 is given. Determine its intersections with the coordinate axes and the vertex of its parabolic graph.
Solution:
With the x-axis: y = 0 With the y-axis : x = 0

18.Determine the coefficients a, b so that the graph of the function f: y = a·log x + b passes through points K, L given that:
Solution:
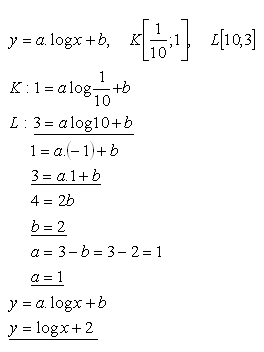
The equation of the logarithmic function is: y = log x + 2.
19.Determine the coefficients a, b so that the function f: y = a2x + b passes through the origin of the coordinate system and the point M [1; 1].
Solution:
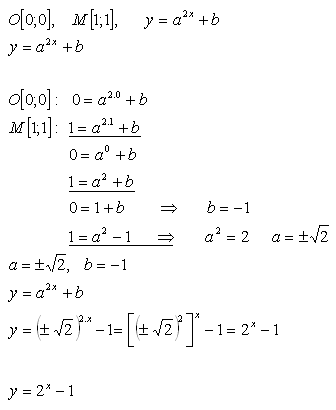
The function has the form f: y = 2x − 1.
20.For which real numbers x do the functions f(x) = (5!)x and g(x) = (4!)x+1 attain the same values?
Solution: