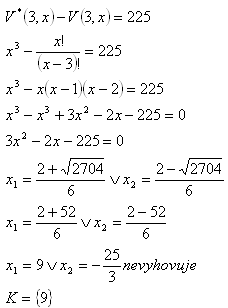Permutations (general)
1.Define and characterize permutations and permutations with repetition.
Solution:
Permutations
A permutation is an ordered sequence of k elements selected from a given finite set of n numbers, without repetitions, and not necessarily using all n elements of the given set.
Number of possible permutations:
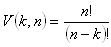
Permutations with repetition
A permutation is an ordered sequence of k elements selected from a given finite set of n numbers, with repetitions, and not necessarily using all n elements of the given set.
Number of possible permutations with repetition:
V*(k,n) = nk
2. From a given set M = {a,b,c,d} enumerate the permutations with and without repetition for k=2. Determine their number.
Solution:
a) Permutations:
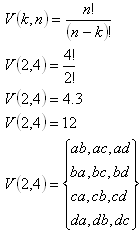
b) Permutations with repetition:
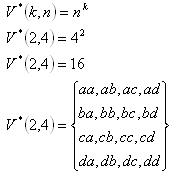
3. There are 7 members in a committee. How many ways are there to choose a chairman, deputy chairman, secretary and a cash keeper?
Solution:
Permutations, n = 7, k = 4
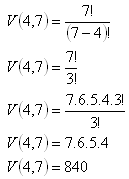
There are 840 ways of choosing the four officials.
4.Eight students promissed to send a postcard each other. How many postcards did they send together?
Solution:
Permutations, n = 8, k = 2
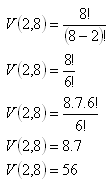
The students sent 56 postcards.
5.From how many numbers 240 permutations can be made if the number of elements to be selected is 2?
Solution:
Permutations, n = x, k = 2
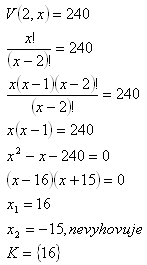
16 numbers are needed.
6.If the number of members increments by 2, the number of possible variations with k=3 increments by 384. How many members are there?
Solution:
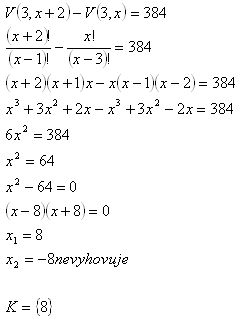
There are 8 members.
7. You have 6 different tickets in your pocket marked with numbers 1-6. How many ways are there to choose 3 of them (considering the order), if
a) the selected ticket is not returned to the pocket.
b) the selected ticket is returned to the pocket.
Solution:
a)
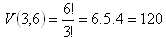
b)
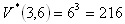
The tickets can be selected in 120 or 216 ways.
8.Number of permutations without repetition with k=3 from x members is lower than number of permutations with repetition with k=3 from x members by 225. How many members are there?
Solution: