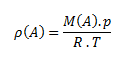Calculations for pure compounds

At the beginning of this chapter, we will focus on the basic relationships needed for chemical calculations. We will define their units, notation, and calculation. I assume basic knowledge of units, chemical and physical concepts.

In chemical practice, we work with different quantities of substances. The amount of a substance can be expressed in terms of the number of particles, the mass of the substance, or its volume.

Amount of substance n determines the quantity of a chemically homogeneous substance according to the number of its basic particles (entities). The unit of the amount of substance is the mole (mol). A mole is the amount of substance in a system that contains exactly as many elementary entities as there are atoms in 0.012 kg (exactly) of the carbon-12 nuclide. The constant giving the number of particles in one mole is Avogadro’s constant N_A = 6.022 × 10²³ mol^-1.

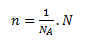
where N_A is the number of particles in one mole of substance and N is any number of particles.

Relative atomic mass A_r of an element expresses the ratio of the average mass of an atom of the element to the atomic mass constant μ = 1.66056 × 10^-27 kg. The atomic mass constant equals 1/12 of the mass of a neutral carbon atom.

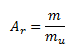
Molar mass is the mass of one mole of a chemically pure substance. In SI, its unit is kg·mol^-1, but in practice g·mol^-1 is most commonly used.

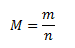
where m is the mass of the substance in grams, n is the amount of substance in moles.

Molar volume of a substance V_m is defined as the ratio of its volume V to the amount of substance n.

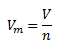
The molar volume of a substance under normal conditions (273.15 K and 101325 Pa) is called the normal molar volume V_mn. In the case of an ideal gas, the value of the normal molar volume is V_mn = 22.41 dm³·mol^-1. (This is Avogadro’s law, according to which equal volumes of different gases at the same pressure and temperature contain the same number of molecules.)

The ideal gas equation is explained in the physics section of the site.

p·V = n·R·T

For an ideal gas, the following laws also apply:

Boyle-Mariotte’s law, according to which the product of pressure and volume of a given quantity of gas at constant temperature is constant

p·V = const, or p₀V₀ = p₁V₁

Gay-Lussac’s law, which expresses the linear increase of gas volume depending on temperature at constant pressure

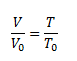
Charles’s law, which expresses the linear increase of gas pressure depending on temperature at constant volume

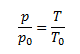
Dalton’s law – the total pressure p of a gaseous mixture is equal to the sum of the partial pressures of all its components

p = ∑p_i at constant temperature

The partial pressure of the i-th component p_i is the pressure the component would have if it alone occupied the entire volume of the system at the given temperature. For the partial pressure of a component:

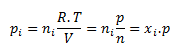
where n_i is the amount of substance of the i-th component, n is the amount of substance of the mixture, and x_i is the mole fraction of the i-th component.

Density of a substance is the ratio of the mass of the substance to its volume. The unit of density in the SI system is kilogram per cubic meter, kg·m^-3, or gram per cubic centimeter g·cm^-3.

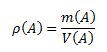
The relation for gas density can be derived from the state equation: