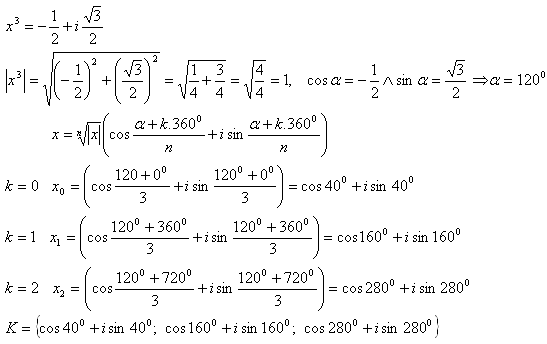Solving equations in the set of complex numbers
1.In the set C solve the equation:
Solution:
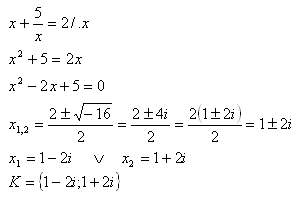
2.In the set C solve the equation:
Solution:
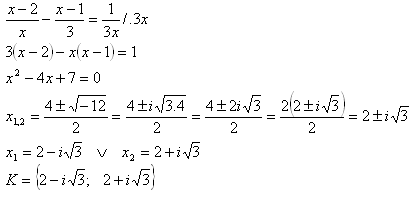
3. In the set C solve the equation:
Solution:
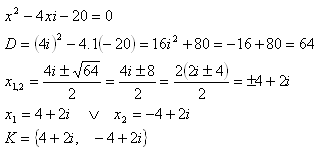
4.Which quadratic equation has one root x1 = 1 – i
Solution:
If x1 = 1 – i, then x2 = 1 + i.
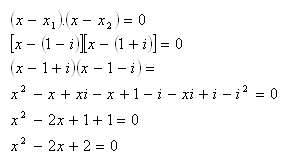
5.Which quadratic equation has roots
Solution:
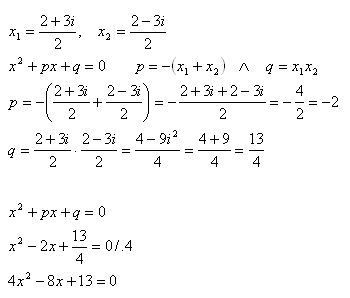
The equation with the given roots is 4x2 - 8x + 13 = 0
6.In the set C solve the equation:
x4 – 1 = 0
Solution:
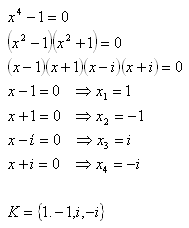
7.In the set C solve the equation:
x6 – 64 = 0
Solution:
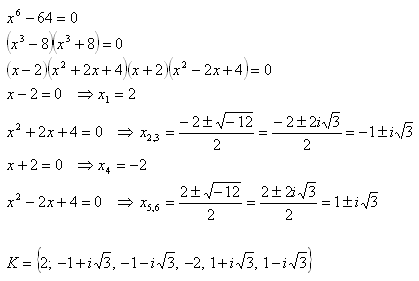
8.In the set C solve the equation:
5x3 – 11x2 + 11x – 5 = 0
Solution:
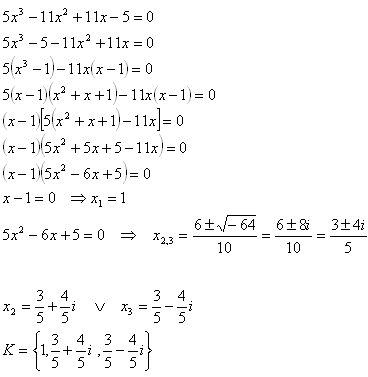
9. In the set C solve the equation x4 – 10x2 = 96. Choose a suitable substitution.
Solution:
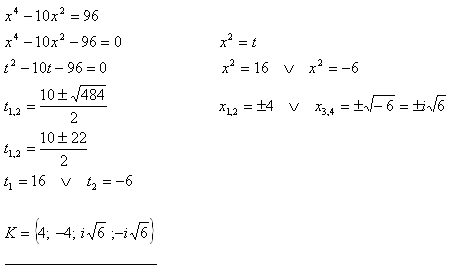
10.In the set C solve the equation 5(x – 3)4 + 8(x – 3)2 = 112. Choose a suitable substitution.
Solution:
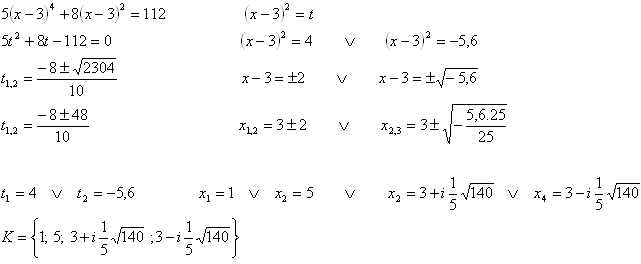
11.In the set C solve the equation:
Solution:
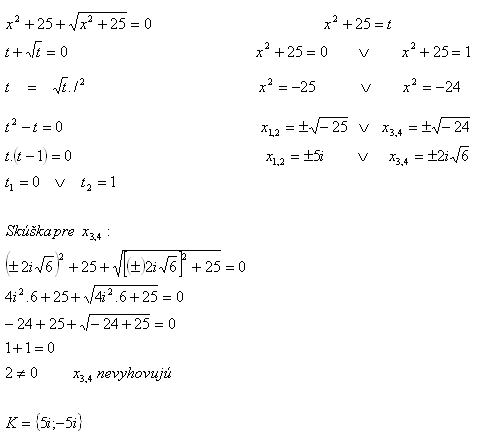
12. In the set C solve the equation x3 – x2 + x = 0. Show that: x1 + x2 + x3 = 1 and x1·x2·x3 = 0
Solution:
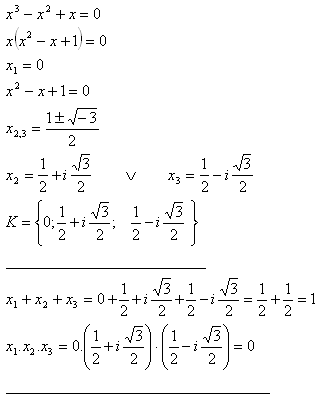
13.In the set C solve the equation 16x4 – 81 = 0. Use the trigonometric (polar) form of a complex number.
Solution:
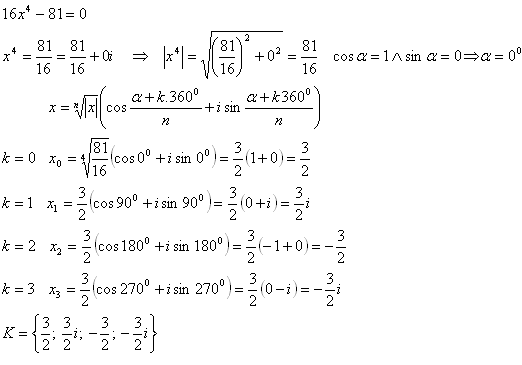
14.In the set C solve the equation x6 + 64 = 0. Use the trigonometric (polar) form of a complex number.
Solution:
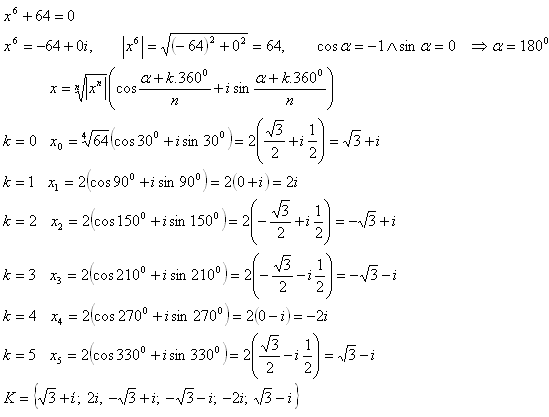
15.In the set C solve the equation:
Solution: