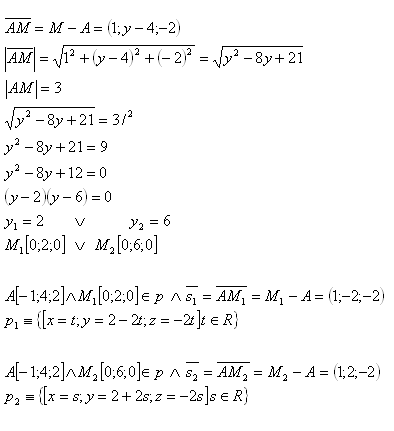Line in space
1. What do we know about the properties of a line in space?
Solution:

2. Write the parametric equation of the line that passes through point A [2;4;-3], parallel to line BC, where B [3;2;-1], C [7;1;9]. Determine which of the points M [-1;2;0], N [6;3;7] lies on this line.
Solution:

The point N [6;3;7] lies on line p.
3. Line p is parallel to line AB if A [4;-7;2], B [-1;3;6]. Determine Yc and Zc so that the point
C [2;Yc;Zc] also lies on this line.
Solution:
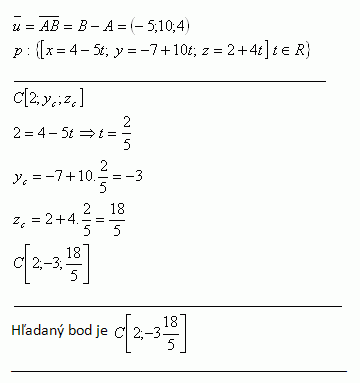
4. Given triangle ΔABC with vertices A [-2;5;4], B [2;3;-1], C [2;7;-2]. Write the parametric equations of the sides of the triangle a = BC, b = AC,
c = AB
Solution:
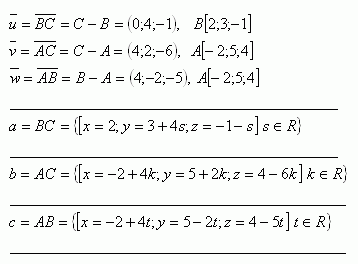
5. Given point M [3;2;-1] and the parametric equation of line p
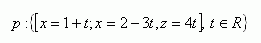
Write:
a) the equations of line q that passes through point M and is parallel to p
b) the equations of line q that passes through point M and is perpendicular to p
c) the equations of line q that is parallel to the y-axis
Solution:
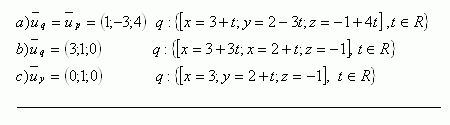
6. Determine the mutual position of the lines whose parametric equations are
Solution:

The lines are skew. (t = 1, s = -4 does not satisfy the y-coordinate)
7. Two lines p and q are given. Determine their mutual position. If they intersect, find their intersection point and the angle between them.
Solution:
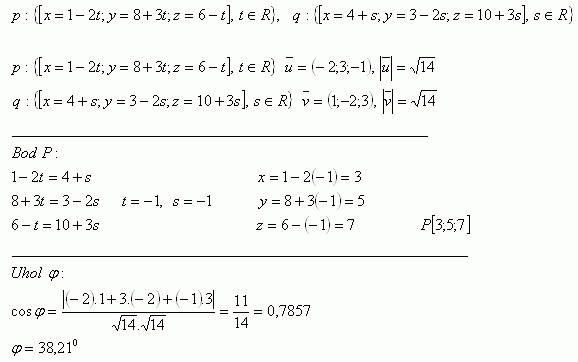
The lines intersect at point P [3;5;7] and form an angle φ = 38.21°.
8. Determine the mutual position of lines p and q, their intersection point and the angle they form. Also calculate the distance from point M [5;-1;4] to the intersection of the lines.
Solution:
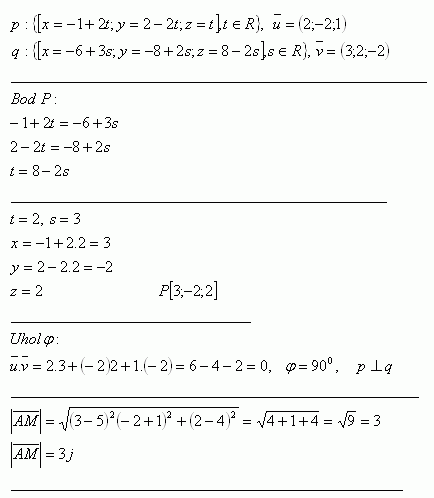
9. Decide which of the points A, B lies on line p, if it holds
Solution:
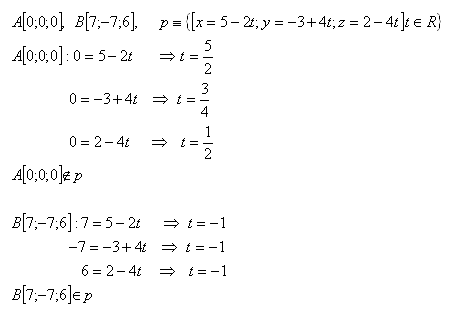
Point B [7;-7;6] lies on line p.
10. Write the parametric equation of the line that passes through points A [3;-7;2], B [5;-4;1] and determine the coordinates x, z of point C [x;2;z] so that it lies on line p.
Solution:
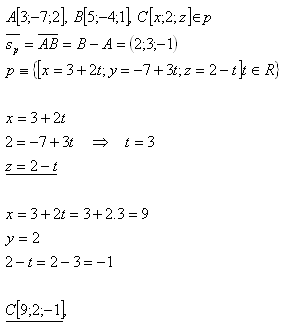
The coordinates of the sought point are C [9;2;-1].
11. Determine the mutual position of lines p and q in space if:
Solution:
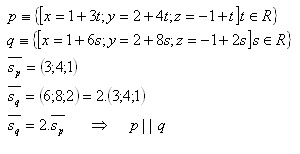
Lines p and q are parallel.
12. Determine the mutual position of lines p and q in space if:
Solution:
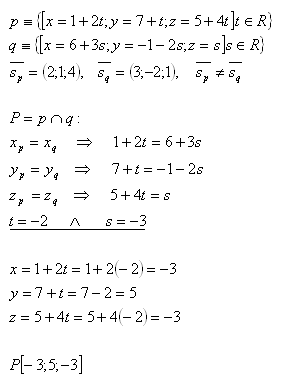
Lines p and q are non-parallel (they intersect). They intersect at point P [-3;5;-3].
13. Determine the angle (inclination) between lines p and q in space if:
Solution:
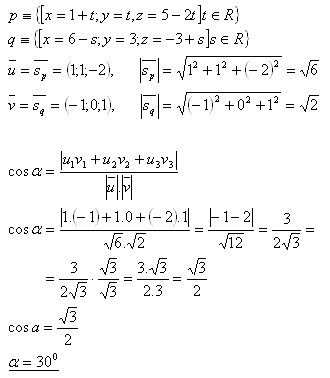
The angle between lines p and q is α = 30°.
14. Determine the angle between lines p and q in space if:
Solution:
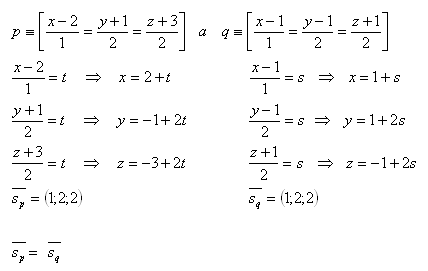
Lines p and q are parallel.
15. Given points A, B, C. Write the parametric equation of line p that passes through the midpoints of segments AB and BC. Solve for the points:
Solution:
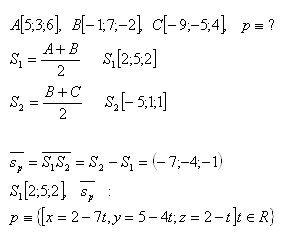
16. Calculate the distance from point M to line p, if:
Solution:

The distance from point M to line p is 6 units.
17. Given lines p and q. Find a vector that is perpendicular to both direction vectors of the given lines. Solve for the lines:
Solution:
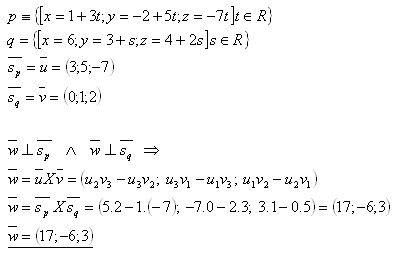
18. Given lines p and q. Determine "m" so that the lines are non-parallel (intersecting). Determine their intersection.
Solve for the lines:
Solution:
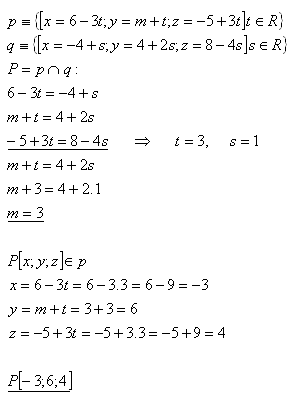
Lines p and q will be non-parallel (intersecting) for m = 3. Their intersection is P [-3;6;4].
19. Calculate the distance from point M to the intersection of lines p and q. Solve for point M [2;3;–23] and the lines:
Solution:

The distance between P and M is 25 units.
20. Given point A [-1;4;2]. On the y-axis determine point M such that |AM| = 3. Also write the parametric equation of line AM.
Solution: