Deformation of solids
1.What should we know about the deformation of solids?
Solution:
Deformation is a change in the shape of a body due to external forces.
Deformation:
- a.) elastic – reversible, temporary
- b.) plastic – non-elastic, permanent
Deformation can be caused by tension, compression, bending, shear, torsion, or a combination.
Tensile deformation:
Absolute elongation:
Δl = l – l0
Relative elongation:
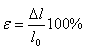
Normal stress:
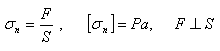
Hooke's law:
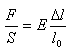
Hooke's law holds only up to the elastic limit.
Stress–strain curve:
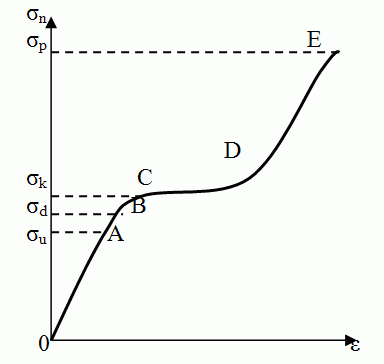
σu = proportional limit
σd = σE = elastic limit (allowable stress)
σk = yield point
σp = ultimate strength
E = Young's modulus in tension
2.Determine whether an iron wire with a diameter of 2 mm will break if it is tensioned by a force of 1 kN. (σE = 314 MPa)
Solution:
Given/Analysis:
d = 2 mm, r = 1 mm = 10-3 m, F = 103 N, σE = 314 MPa
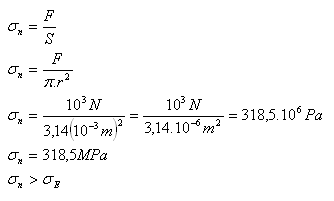
Because σn > σE, the iron wire will break.
3.Calculate the relative elongation of a rope with an original length of 10 m if it elongates by 40 mm during deformation.
Solution:
Given/Analysis:
l0 = 10 m, Δl = 40 mm = 0.04 m
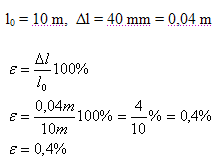
The relative elongation of the rope is ε = 0.4%.
4.How does the normal stress in a wire change if the tensile force acting on the wire increases 4 times and the wire diameter 2 times?
Solution:
Given/Analysis:
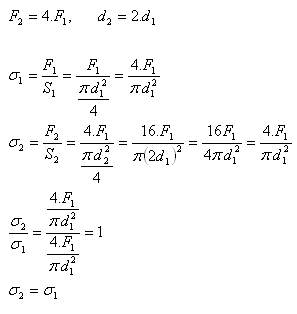
The normal stress in the wire does not change.
5.What must be the radius of a copper wire (σp = 2·108 Pa) so that it does not break under a force of 500 N?
Solution:
Given/Analysis:
F = 500 N, σp = 2·108 Pa
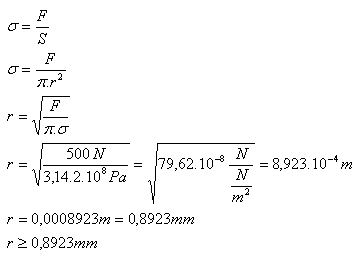
The wire radius must satisfy r >= 0.89 mm.
6.What is the maximum length an iron wire can have when hung vertically so that it does not break under its own weight?
Solution:
Given/Analysis:
g = 9.81 m·s-2, ρ(Fe) = 7800 kg·m-3 = 7.8·103 kg·m-3, σp = 314·106 Pa
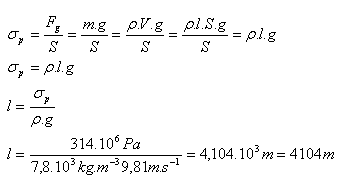
The length of the wire can be at most 4104 m.
7.What is the tensile force in a guitar string of length 0.65 m and cross-sectional area 0.325 mm2 if it elongated by 5 mm during tightening? (E = 220 GPa)
Solution:
Given/Analysis:
l0 = 0.65 m, Δl = 5·10-3 m, S = 0.325·10-6 m2, E = 220·109 Pa
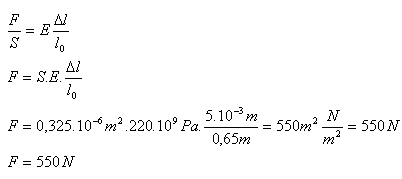
The guitar string is tensioned by a force F = 550 N.
8. An aluminum wire with original length 4.2 m and diameter 1.1 mm elongated by 15.2 mm under a force of 0.23 kN. Determine the Young's modulus in tension E.
Solution:
Given/Analysis:
l0 = 4.2 m, r = 0.55·10-3 m, F = 0.23·103 N, Δl = 15.2·10-3 m

The Young's modulus in tension for aluminum is E(Al) = 67 GPa.
9.At the end of a vertical steel rod (E = 220 GPa) of length 1.5 m, a 500 kg weight is to be suspended. What rod diameter should we choose if we want the elongation after loading to be no more than 0.3 mm? (Neglect the rod’s own weight.)
Solution:
Given/Analysis:
l0 = 1.5 m, m = 500 kg, Δl = 3·10-4 m, E = 220 GPa = 220·109 Pa, g = 10 m·s-2
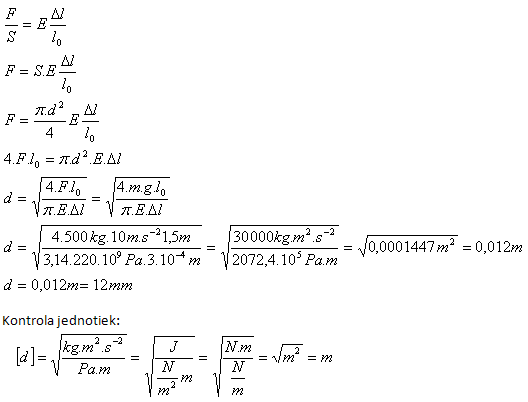
We choose a rod diameter d = 12 mm.
10.Determine the work required to elastically stretch a steel rod (E = 220 GPa) of length 1 m and cross-section 1 cm2 by 1 mm in tension.
Solution:
Given/Analysis:
l0 = 1 m, Δl = 1 mm = 1·10-3 m, S = 1 cm2 = 1·10-4 m2, E = 220·109 Pa
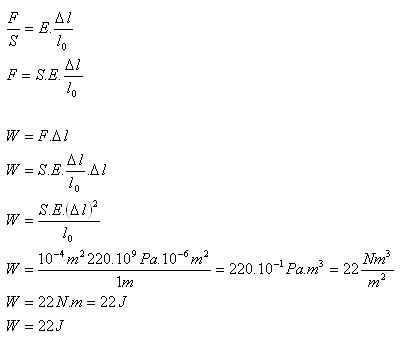
To stretch the steel rod, the required work is W = 22 J.