Cutting an apple

Greek philosopher Democritus of Abdera (around 460 – 370 BC) believed in the existence of atoms. Legend says that Democritus once sat by the sea, held an apple in his hand, and thought: “If I cut this apple into two parts, I get half an apple; if I cut this half again into two parts, I get a quarter of an apple. If I continue dividing this way, I get an eighth, a sixteenth of the apple, etc. How many times must I divide the apple in this way until I reach its smallest, further indivisible part – the atom?”

Here is the answer:

Let’s assume that Democritus’ apple had a volume of about 1dm³, which is 10^–3m³. Its volume after n-fold division is 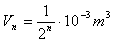   which is at the same time the volume of a single atom. Austrian physicist J. Loschmidt (1824 – 1895) found that the diameter of an atom is about  10^–10m, so the volume of an atom is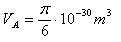  

 

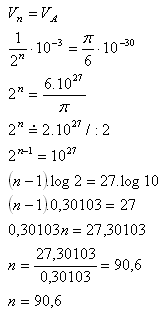
Already after the 90th division of the apple, Democritus would have reached his goal.

---