Electric current in metals
1.When starting the electric rack railway train, a current of 500A is drawn from the line. Determine the total electric charge transferred by free electrons in 1 minute. How many electrons passed through the conductor? e = 1.602·10-19C.
Solution:
Analysis:
I = 500A, t = 60s, e = 1.602·10-19C Q = ?, n = ?
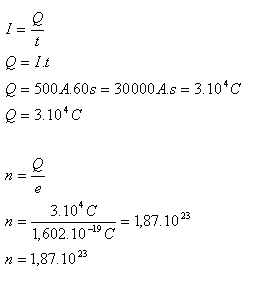
The total electric charge transferred by electrons is Q = 3·104C. 1.87·1023 electrons passed through the conductor.
2.The copper telegraph cable (ρ = 0.017·10-6Ω·m) between Snina and Humenné had a cross-section of 8mm2 and a resistance of 46.75Ω. What was its length?
Solution:
Analysis:
S = 8·10-6m2, R = 46.75 Ω, ρ = 0.017·10-6Ω·m, l = ?
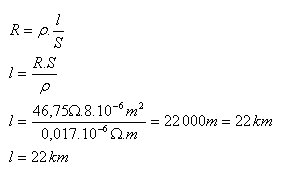
The cable was 22 km long.
3.A nickel wire (ρ1 = 0.4·10-6Ω·m) has a length l1 = 1.25m. What length should a constantan wire (ρ2 = 0.5·10-6Ω·m) of the same cross-section and the same ohmic resistance have?
Solution:
Analysis:
l1 = 1.25m, ρ1 = 0.4·10-6Ω·m, ρ2 = 0.5·10-6Ω·m, l2 = ?
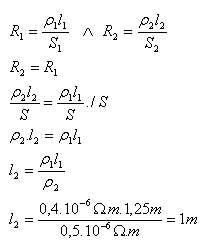
The length of the constantan wire would be l2 = 1m.
4.A platinum resistance thermometer (α = 3.9·10-3K-1) has a resistance of 500Ω at 20°C. The resistance of the thermometer in a heated furnace is 2500Ω. What is the temperature of the furnace?
Solution:
Analysis:
R20 = 500Ω, Rt = 2500Ω, α = 3.9·10-3K-1, t1 = 20°C, Δt = ?, t2 = ?
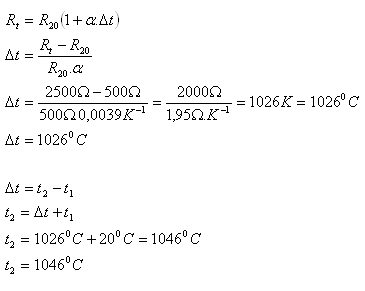
The temperature of the heated furnace is 1046°C.
5.A copper wire (ρ1 = 0.02·10-6Ω·m) with a diameter d1 = 4mm needs to be replaced with an aluminum wire (ρ2 = 0.03·10-6Ω·m) of the same length. How thick should the aluminum wire be to keep the resistance unchanged?
Solution:
Analysis:
d1 = 4·10-3m, ρ1 = 0.02·10-6Ω·m, ρ2 = 0.03·10-6Ω·m, d2 = ?
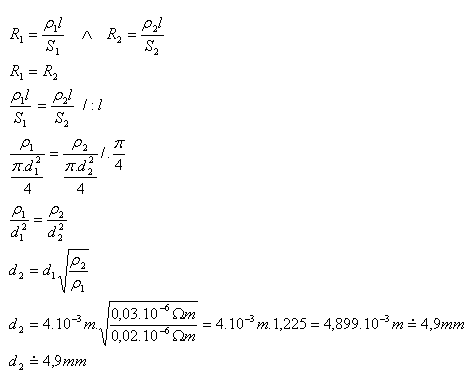
The aluminum wire must be approximately 4.9mm thick.
6.Two resistors R1, R2 in series have a total resistance of 5 Ω, and in parallel 1.2 Ω. What are the resistances of the individual resistors?
Solution:
Analysis:
R1 = x, R2 = y
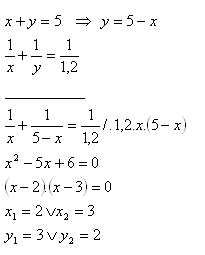
The resistances are R1 = 2 Ω and R2 = 3 Ω, or R1 = 3 Ω and R2 = 2 Ω.
7.A resistor with resistance R = 3.8 Ω is connected to an EMF source Ue = 12V. The current through the circuit is I = 3A. Determine the internal resistance, terminal voltage, and maximum current.
Solution:
Analysis:
R = 3.8Ω, Ue = 12V, I = 3A, Ri = ?, U = ?, Imax=?
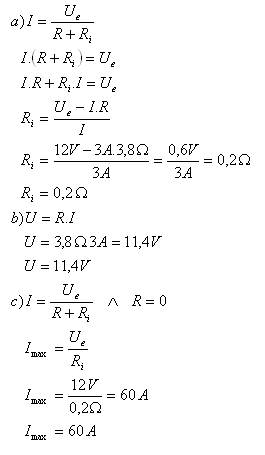
The internal resistance is Ri = 0.2 Ω, terminal voltage U = 11.4V, and maximum (short-circuit) current Imax = 60A.
8.A 15V EMF source with an internal resistance of 5 Ω is connected to a resistor with resistance 10 Ω. A capacitor with capacitance 1μF is connected in parallel to the source terminals. Determine the charge on the capacitor.
Solution:
Analysis:
R = 10 Ω, Ri = 5 Ω, Ue = 15 V, C = 10-6F, Q = ?
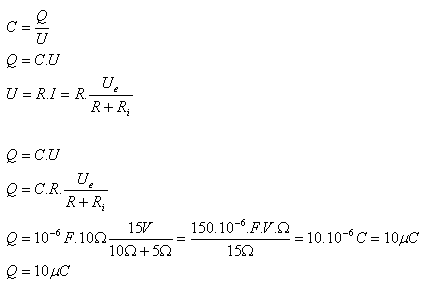
The charge on the capacitor is Q = 10 μC.