Lenses

Solution:

A lens is a homogeneous body bounded by:

• two spherical surfaces

• a spherical surface and a plane

A lens forms an image by refraction of light. There are two types of lenses:

• converging (convex)

• diverging (concave)

Thin lens with equal radii of curvature:

• f = focal length

• r = 2·f = radius of curvature

• a = object distance

• á = image distance

• y = object height

• ý = image height

Magnification of the image:

Object space = space in front of the lens (left side)
Image space = space behind the lens (right side)

Sign convention:

• r₁, r₂ positive (negative) – spherical surfaces convex (concave)

• a positive – object in the object space

• á positive (negative) – image in the image (object) space

• y, ý positive (negative) – above (below) the optical axis

Lens equation:

$$\frac{1}{a}+\frac{1}{\widehat{a}}=\frac{1}{f}$$

$$\frac{1}{a} + \frac{1}{\hat{a}} = \frac{1}{f}$$$$\frac{1}{f} = \left(\frac{n_2}{n_1} - 1\right)\left(\frac{1}{r_1} - \frac{1}{r_2}\right)$$

n₂ = refractive index of the lens, n₁ = refractive index of the surrounding medium

Optical power of a lens Φ:

• Φ > 0 → converging lens

• Φ < 0 → diverging lens

Solution:

Analysis:

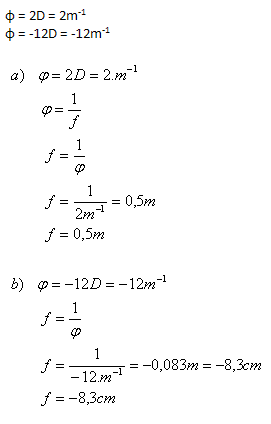
The focal length of the lenses is 0.5m and –8.3cm.

Solution:

Analysis:

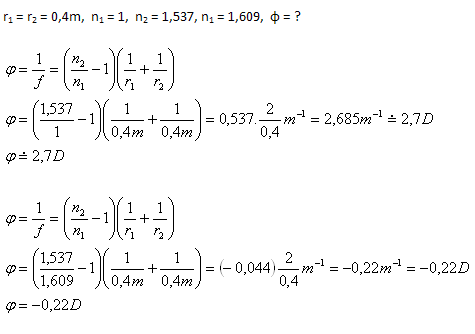
The optical power of the lens in air is 2.7D, in carbon disulfide –0.22D.

Solution:

Analysis:

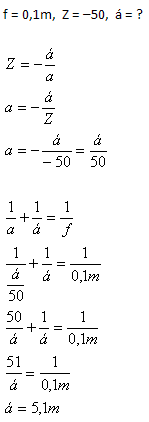
The projection screen should be placed 5.1m from the objective.

Solution:

Analysis:

a = distance from the candle to the lens
á = distance from the lens to the wall
a + á = 100cm, f = 9cm

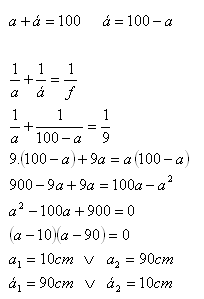
The lens should be placed 10cm from the candle and 90cm from the wall (or vice versa).

Solution:

Analysis:

y₁​=5 cm,y₁′​=15 cm,y₂​=5 cm,y₂′​=10 cm,f=?

Before shifting:

$$|Z_1| = \frac{y'_1}{y_1} = \frac{15\text{ cm}}{5\text{ cm}} = 3, \qquad a'_1 = 3a, \qquad a = \text{object distance}$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{a_1} + \frac{1}{a'_1} = \frac{1}{f}$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{a} + \frac{1}{3a} = \frac{1}{f}$$

After shifting:

$$|Z_2| = \frac{y'_2}{y_2} = \frac{10\text{ cm}}{5\text{ cm}} = 2, \qquad a_2 = a + 1.5, \qquad a'_2 = 2a_2 = 2(a + 1.5)$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{a_2} + \frac{1}{a'_2} = \frac{1}{f}$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{a + 1.5} + \frac{1}{2(a + 1.5)} = \frac{1}{f}$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{f} = \frac{1}{f}$$$$\frac{\mathrm{}}{}$$

$$\frac{1}{a}+\frac{1}{3a}=\frac{1}{a+1.5}+\frac{1}{2(a+1.5)}$$

$$\frac{1}{a} + \frac{1}{3a} = \frac{1}{a + 1.5} + \frac{1}{2(a + 1.5)}$$$$\frac{4}{3a} = \frac{3}{2(a + 1.5)}$$$$\mathrm{}$$

$$8(a + 1.5) = 9a$$$$$$

$$a = 12\text{ cm}, \qquad \frac{1}{f} = \frac{4}{3a}$$$$$$

$$f = \frac{3a}{4} = \frac{3 \cdot 12\text{ cm}}{4} = 9\text{ cm}$$$$$$

$$f = 9\text{ cm$$

The focal length of the lens is f = 9cm.

Solution:

Analysis:

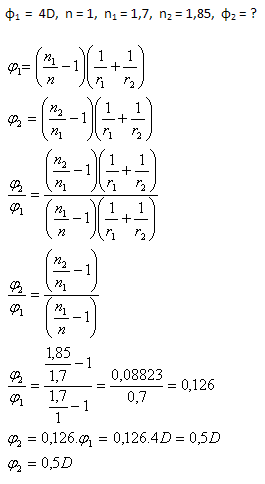
The optical power of the lens in the liquid is φ = 0.5D. It is a convex lens.

Solution:

Analysis:

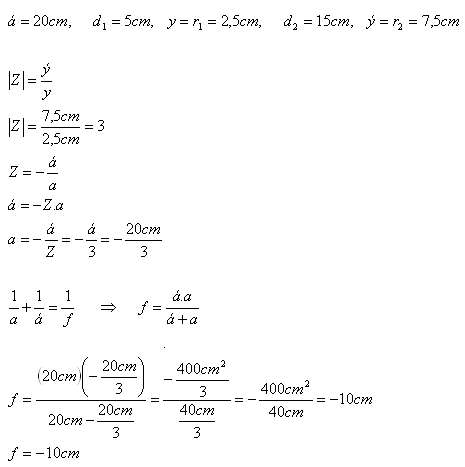
The focal length of the concave lens is f = –10cm.

Solution:

Analysis:

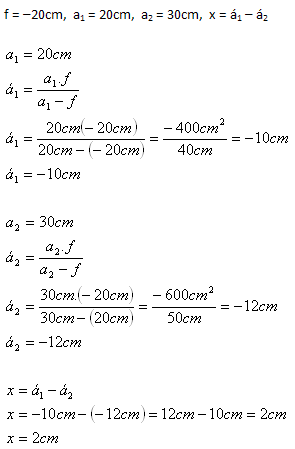
The distance between the images formed by the concave lens is x = 2cm.

Solution:

Analysis:

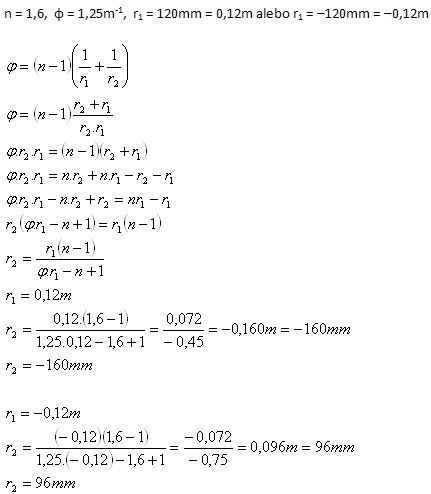
• If r₁ = 120mm, then r₂ = –160mm.
• If r₁ = –120mm, then r₂ = 96mm.