sk|cz|de|

Physics

Electromagnetic waves

1. Characterize the nature and properties of electromagnetic waves.

Solution:

Every change in the magnetic field induces a varying electric field. Every change in the electric field induces a varying magnetic field. The magnetic and electric fields always exist simultaneously and form an electromagnetic field, which propagates through space at a speed of c = 3.108 m.s-1.

Phase velocity of electromagnetic wave is:

v=1εμv = \frac{1}{\sqrt{\varepsilon \mu}}

A progressive electromagnetic wave is characterized by the equation:

u=Umsin⁡(2π(tT−xλ)),λ=cT=cfu = U_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad \lambda = cT = \frac{c}{f} i=Imsin⁡(2π(tT−xλ)),x=distance from sourcei = I_m \sin \left(2\pi\left(\frac{t}{T} - \frac{x}{\lambda}\right)\right), \quad x = \text{distance from source}

A dipole (radiator, antenna) is an open oscillating LC circuit that emits (receives) electromagnetic waves.

Half-wave radiator:

l=λ2=c2fl = \frac{\lambda}{2} = \frac{c}{2f}

Electromagnetic wave does not propagate along the conductors but arises between the conductors.

Two conductors can be connected:

  • Short-circuited – at the end of the line a conductor is connected; there is zero voltage and a current antinode.

  • Open-circuited – at the end of the line no conductor is connected; there is a voltage antinode and a current node.

The interference of the original and reflected wave arises between the conductors → “standing electromagnetic wave”

Amplitudes of standing electromagnetic wave:


Rλ Voltage Current
Short-circuited R→0R \to 0,     λ=4l\lambda    U0=2Umsin⁡2πxλU_0 = 2U_m \sin \frac{2\pi x}{\lambda}     I0=2Imcos⁡2πxλI_0 = 2I_m \cos \frac{2\pi x}{\lambda}
Open-circuited R→∞,     λ=2l\lambda    U0=2Umcos⁡2πxλU_0 = 2U_m \cos \frac{2\pi x}{\lambda}     I0=2Imsin⁡2πxλI_0 = 2I_m \sin \frac{2\pi x}{\lambda}

 

2.Characterize the individual types of electromagnetic radiation.

  1. Radio radiation
  2. Microwaves
  3. Infrared radiation
  4. Visible light
  5. Ultraviolet radiation
  6. X-ray radiation
  7. Gamma radiation
  8. Cosmic radiation

Solution:


  • Radio radiation: f=105 Hz–109 Hz, (λ=102 m–10−1 m)f = 10^{5}\,\text{Hz} – 10^{9}\,\text{Hz}, \; (\lambda = 10^{2}\,\text{m} – 10^{-1}\,\text{m})
    Used for sound and image transmission – radio, television, radar.

    Microwaves: f=109 Hz–1012 Hz, (λ=10−1 m–10−4 m)f = 10^{9}\,\text{Hz} – 10^{12}\,\text{Hz}, \; (\lambda = 10^{-1}\,\text{m} – 10^{-4}\,\text{m})
    Thermal vibrations of atoms and molecules.

    Infrared radiation: f=1012 Hz–1014 Hz, (λ=10−4 m–10−5 Hz)
    Sources are warm bodies – the Sun, heated metal, etc. Used as a heat source, in microwaves, remote controls, photography in the dark.

    Visible light: f=3.8⋅1014 Hz–7.8⋅1014 Hz, λ=7.9⋅10−7 m–3.86⋅10−7 m

    Ultraviolet radiation: f=1015 Hz–1016 Hz, (λ=10−7 m–10−8 m)
    The Sun, mercury vapor lamps, electric arcs. Causes tanning of the skin, kills bacteria, at high doses causes skin cancer. Used in so-called “mountain sunlamps.”

    X-ray radiation: f=1016 Hz–1020 Hz, (λ=10−8 m–10−12 m)
    Produced when cathode rays strike an anode target. Used in medicine for diagnosis.

    Gamma radiation: f=1020 Hz–1024 Hz, (λ=10−12 m–10−16 m)
    Very strong penetrating radiation; at small doses it treats cancer, at high doses it arises from nuclear explosions, decay of atomic nuclei, and atomic bombs.

    Cosmic radiation: f=1024 Hz ⇒ (λ=10−16 m)
    A stream of protons or photons falling to Earth from space.

    •  

    3.Calculate the speed of electromagnetic waves in a vacuum and in water, given that for water εr=81, μr = 1.

    Solution:

    Analysis:

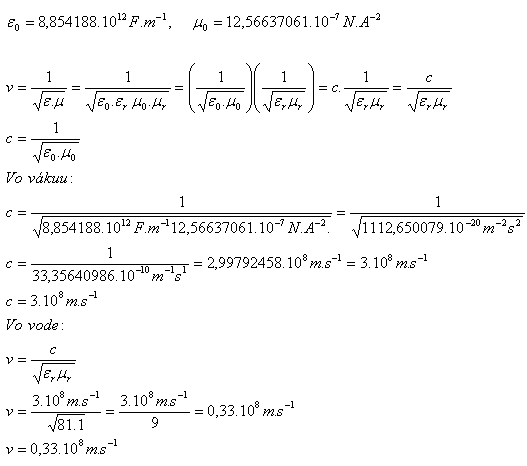
    fyzika-elektromagneticke-vlnenie-3.gif 

    The speed of electromagnetic waves in a vacuum is c = 3.108 m.s-1, and in water v = 0,33.108 m.s-1.

    4.The VHF radio communication band has a frequency range of 66 MHz to 73 MHz. Determine the smallest and largest wavelength of electromagnetic waves in this band.

    Solution:

    Analysis:

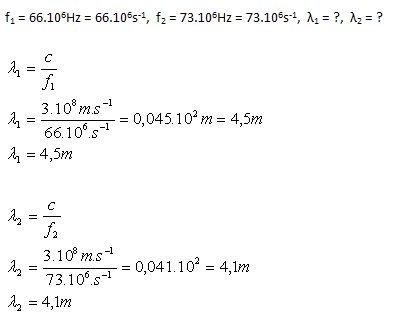
    fyzika-elektromagneticke-vlnenie-4.gif 

    The wavelength range in the VHF radio communication band is from 4.1 m to 4.5 m.

    5.Determine the length of a half-wave dipole that has capacitance 10 pF and inductance 0.9 μH. (c = 3.108 m.s-1)

    Solution:

    Analysis:

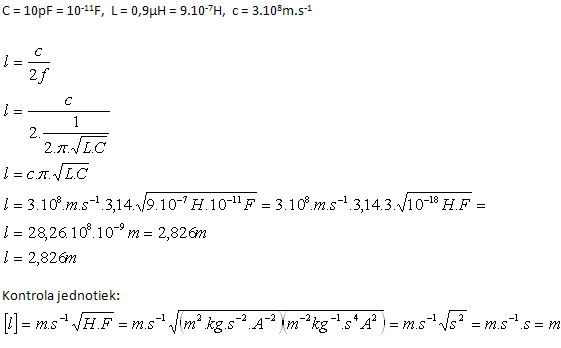
    fyzika-elektromagneticke-vlnenie-5.gif 

    The half-wave dipole has length l = 2.826 m.

    6.The resonant circuit of a receiver is tuned to receive a transmission carried by electromagnetic waves with a wavelength of 5 m. Determine the inductance of the coil in the resonant circuit if its capacitance is 20 pF.

    Solution:

    Analysis:

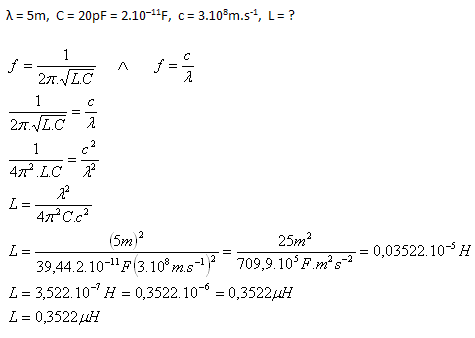
    fyzika-elektromagneticke-vlnenie-6.gif 

    The inductance of the coil in the resonant circuit is 0.3522 μH.

    7.The resonant circuit of a transmitter consists of a coil with L = 50 μH and a capacitor whose capacitance can be varied from 60 pF to 240 pF. Determine the interval of wavelengths of the electromagnetic waves in which the transmitter operates.

    Solution:

    Analysis:

    fyzika-elektromagneticke-vlnenie-7.gif 

    The transmitter operates over a wavelength interval from 103.2 m to 206.3 m.

    8.A very long two-wire transmission line is connected to an AC voltage source with amplitude 1 V and frequency 75 MHz. Determine the instantaneous voltage between the wires at a distance of 5.5 m from the source at the moment when the source voltage is zero.

    Solution:

    Analysis:

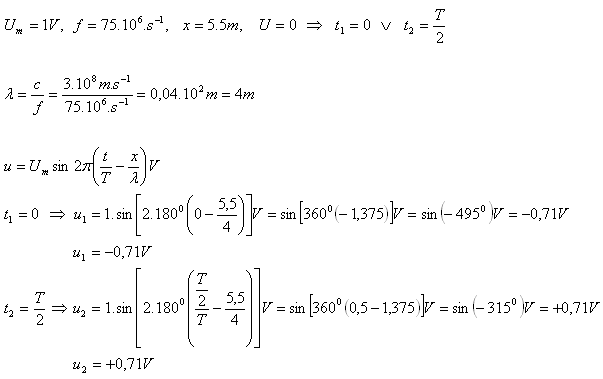
    fyzika-elektromagneticke-vlnenie-8.gif 

    The instantaneous voltages are u1 = –0.71 V and u2 = 0.71 V.

    9.A standing electromagnetic wave is formed between two long conductors. The conductors are open-circuited. At what distance from the ends of the conductors will there be

    • a) a current antinode of the standing electromagnetic wave
    • b) a current node of the standing electromagnetic wave

    Solution:

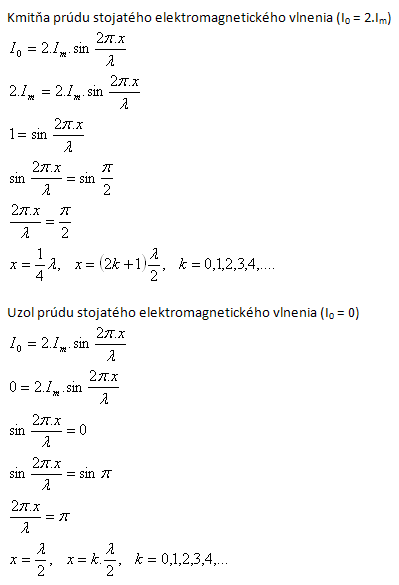
    fyzika-elektromagneticke-vlnenie-9.gif

    10.An electromagnetic dipole for reception in air has length l = 1.8 m. Determine its length for receiving electromagnetic waves of the same frequency in water. (εr = 81, μr = 1)

    Solution:

    Analysis:

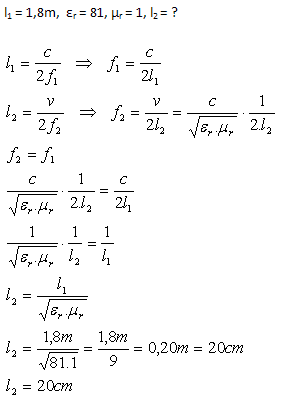
     fyzika-elektromagneticke-vlnenie-10.gif

    The length of the electromagnetic dipole in water is 20 cm.

    11. One resonant circuit is characterized by L1 = 3.10-3 H and C1 = 2.10-6 F, the other by L2 = 4.10-3 H and C2 = 1.10-6 F.

    • Are the circuits in resonance?
    • If not, make a correction.

    Solution:

    Analysis:

    L1 = 3.10-3 H and C1 = 2.10-6 F, L2 = 4.10-3 H and C2 = 1.10-6 F.

    Condition for resonance:
    L1·C1 = L2·C2
    3.10-3 H · 2.10-6 F = 4.10-3 H · 1.10-6 F
    6.10-6 H·F = 4.10-9 H·F — not valid

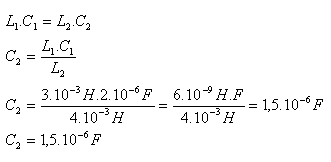
     fyzika-elektromagneticke-vlnenie-11.gif

    The circuits are not in resonance. There are several ways to fix this. For example, replace capacitor C2 = 1.10-6 F with another capacitor C2 = 1.5.10-6 F.

    12.Radio electromagnetic waves with wavelength λ1 = 375 m strike the interface of two media. The angle of incidence is α = 350, the angle of refraction β = 330. What is the wavelength of these waves λ2 in the second medium?

    Solution:

    Analysis:

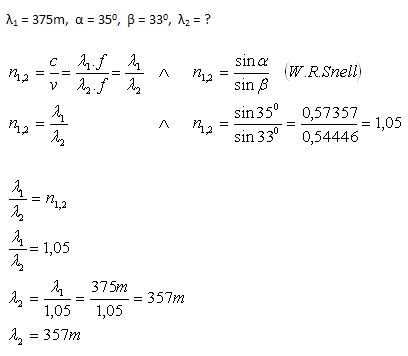
    fyzika-elektromagneticke-vlnenie-12.gif 

    The wavelength in the second medium is λ2 = 357 m.

    13. Let’s have some fun with a small test:

    1. What time elapses between sending and receiving the reflected radar signal from an aircraft that is flying at a distance of 9 km from the radar?

    A) 40 μs
    B) 60 μs
    C) 80 μs

    2. During the Moon radar measurement in 1946, a pulse sent from Earth and reflected from the Moon’s surface returned to Earth in 2.563 seconds. The average distance from Earth to the Moon is:

    A) 834,250 km
    B) 428,350 km
    C) 384,500 km

    3. The wavelength of a transmitter during experiments is 3 cm. The frequency of this wave is:

    A) 10 GHz
    B) 6 GHz
    C) 8 GHz

    4. An LC oscillation circuit with inductance L = 0.5 mH oscillates at frequency f = 1 MHz. The capacitance of its capacitor is:

    A) 30 pF
    B) 40 pF
    C) 50 pF

    5. Electromagnetic radiation with frequency f = 5.2 × 10¹⁴ Hz is:

    A) gamma radiation
    B) visible light
    C) X-rays

    6. The unit m²·kg·s⁻²·A⁻² represents:

    A) henry
    B) farad
    C) weber

    7. The unit m⁻²·kg⁻¹·s⁴·A² represents:

    A) henry
    B) farad
    C) weber

    8. In a radio receiver, we tune by changing the area between the stator and rotor of the tuning capacitor. If we want to tune to a longer wavelength, we must change this area:

    A) not change it
    B) decrease it
    C) increase it 

    Solution:

    1B, 2C, 3A, 4C, 5B, 6A, 7B, 8C

    14. At what distance from the antenna of a radar is the observed object if the reflected signal returns after 200 μs? Determine the maximum pulse frequency of the radar.

    Solution:

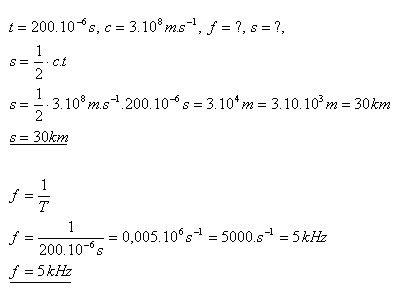
     elektromagneticke-vlnenie-14

    • The observed object is 30 km from the radar antenna.
    • The maximum frequency of the radar is f = 5 kHz.

    15. In television, 25 images per second are replaced, each consisting of 625 lines. At what speed does the light spot move across the screen of a television receiver whose line is 0.14 m long?
    (Neglect the return path of the beam.)

    Solution:

    In 1 second:

    • a.) images ................25
    • b.) lines....................25·625 = 15625 lines
    • c.) meters.....................15625·0.14 m = 2187.5 m
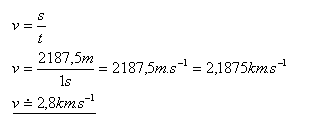
    elektromagneticke-vlnenie-15

     The light spot moves across the screen with a speed v = 2.8 km·s-1

    16. Calculate the frequency of an electromagnetic wave that propagates in air with a wavelength λ = 240 m. How will the wavelength change if it enters a homogeneous medium where it propagates at a speed of 2·108 m·s–1? ( f1 = f2 )

    Solution: 
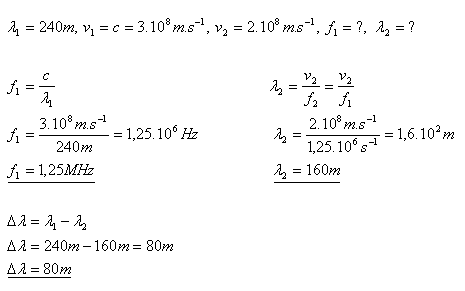
    elektromagneticke-vlnenie-16

    The wavelength decreases by 80 meters.

    17. Determine the fundamental frequency of a standing electromagnetic wave in an open two-wire line of length l = 1.5 m that is immersed in oil.

    Solution:

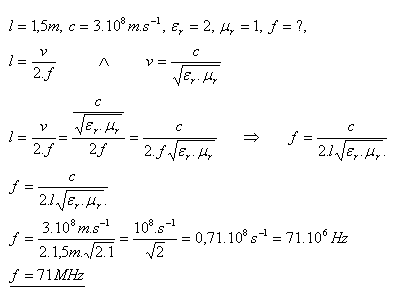
    elektromagneticke-vlnenie-17 

    The frequency of the standing wave in oil is 71 MHz.  

    18. An open two-wire transmission line is connected to a high-frequency voltage source with frequency 400 MHz. What length must the line have so that four nodes of the wave are formed on it? (At the point where it is connected to the source there is a voltage antinode.)

    Solution:

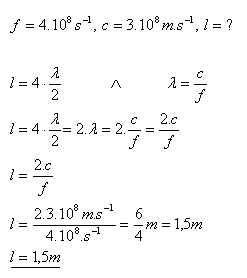
    elektromagneticke-vlnenie-18

    The line must have a length l = 1.5 meters.

    19. An open two-wire transmission line has a length l = 12 m. Determine how many times smaller the voltage and current amplitudes are in a standing wave at a distance x = 5 m from the end of the line compared to the amplitudes at the antinodes. (l = λ/2).

    Solution:

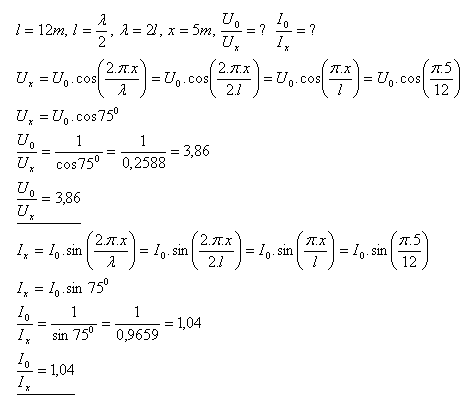
    elektromagneticke-vlnenie-19.gif 

    The amplitude ratios are: U0/Ux = 3.86,   I0/Ix = 1.04

    20. A test transmitter radiates electromagnetic waves with frequency f = 428 MHz. At a distance l = 3.5 m from the transmitter dipole, a reflecting plate is placed. Along the line between the reflector and the transmitter dipole, a technician moves the receiver dipole. How many times does the signal weaken and strengthen again during this movement? (How many times λ/2 fits into l.)

    Solution:

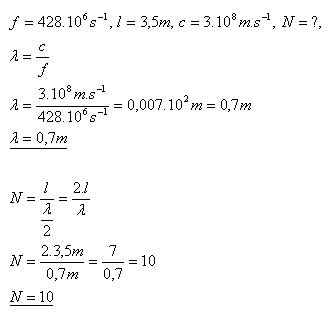
    elektromagneticke-vlnenie-20 

    The signal weakens and strengthens again 10 times.

    21. According to international agreement, ships transmit emergency calls SOS at a wavelength of 600 m. Determine whether an antenna with capacitance C = 400 pF and an inductor with inductance L = 253 μH can be used for this transmission.

    Solution:

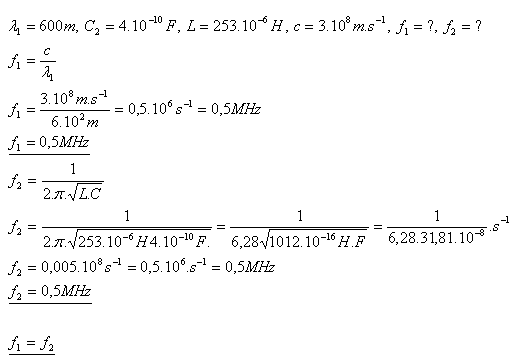
     elektromagneticke-vlnenie-21.gif

    The antenna can be used because f1 = f2 = 0.5 MHz.