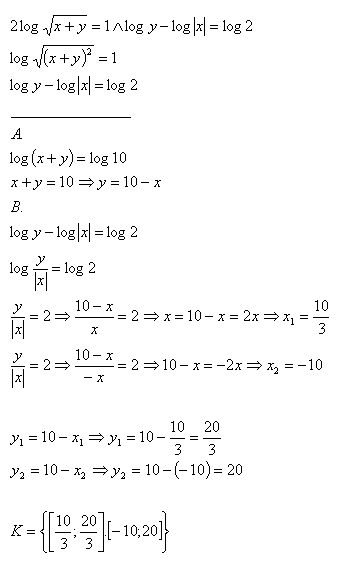Sets of Logarithmic Equations
1. Solve the set of equations:
x + y = 34
log2x + log2y = 6 x,y >0 , x < 34
Solution:
x + y = 34
log2x + log2y = 6 x,y >0 , x < 34
y = 34 -x
log2x + log2(34 – x) = 6
log2 ( x.(34 – x)) = log264
x.(34 –x) = 64
x2 – 34x + 64 = 0
(x- 32)( x-2) = 0
x1 = 32 v x2 = 2
y = 34 – x
y1 = 34 – 32 v y2 = 34 - 2
y1 = 2 v y2 = 32
K = {[32,2][2,32]}
2.Solve the set of equations:
Solution:
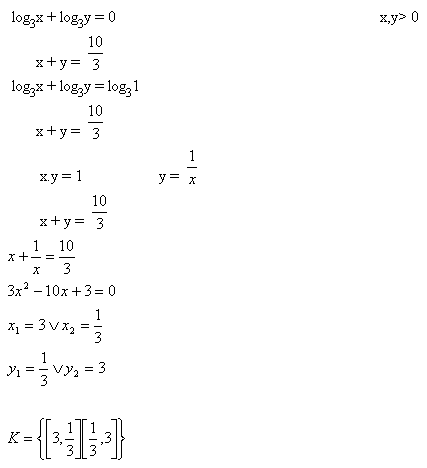
3.Solve the set of equations:
Solution:
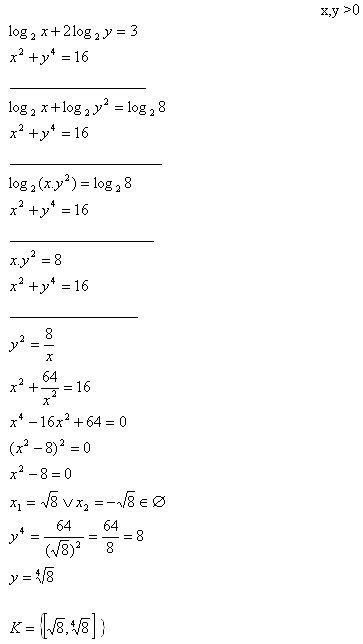
4.Solve the set of equations:
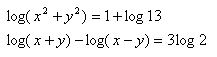
x>0, y>0, x>y
Solution:
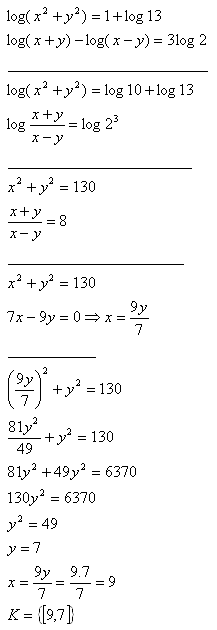
5.Solve the set of equations:
Solution:
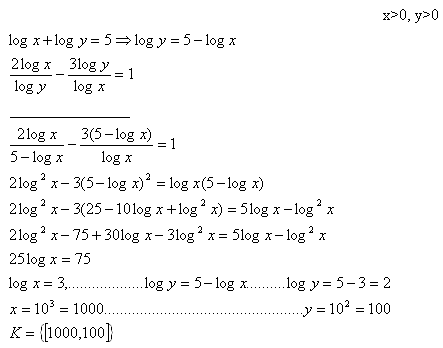
6.Solve the set of equations:
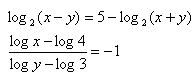
x>0, y>0
Solution:
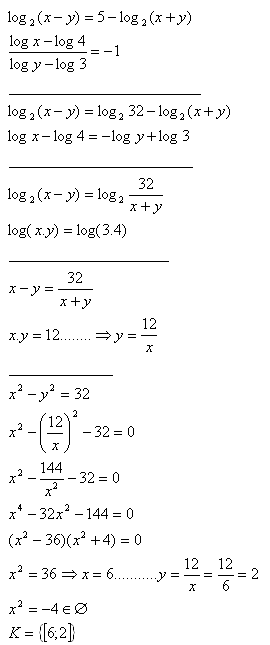
7.Solve the set of equations:
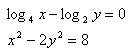
x>0, y>0
Solution:
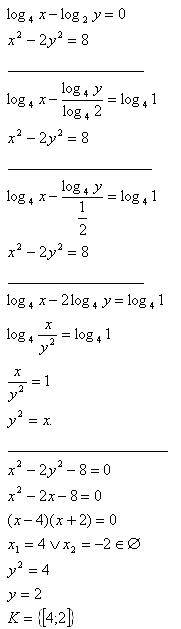
8.Solve the set of equations:
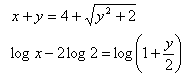
x > 0; y > 0
Solution:
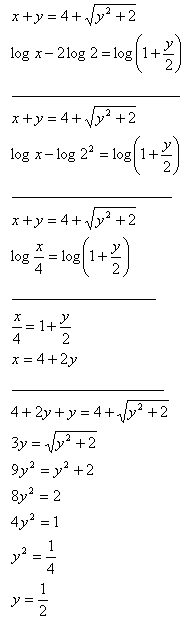
x = 4 + 2y
x = 4 + 2.0,5
x = 4 + 1
x = 5
K = {5;1/2}
9.Solve the set of equations:
Solution:
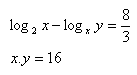
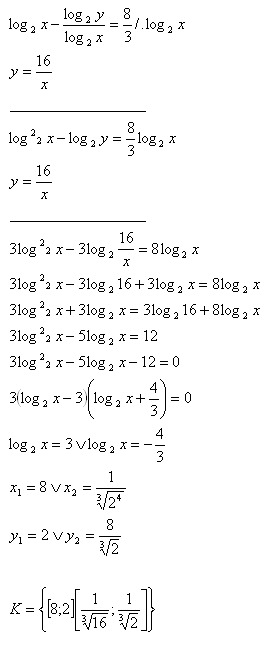
10.Solve the set of equations:
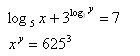
x > 0 ; y> 0
Use the formula: 3
log3y = y
Solution:
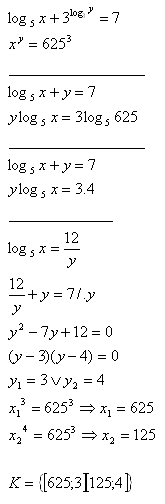
11.Solve the set of equations:
Solution:
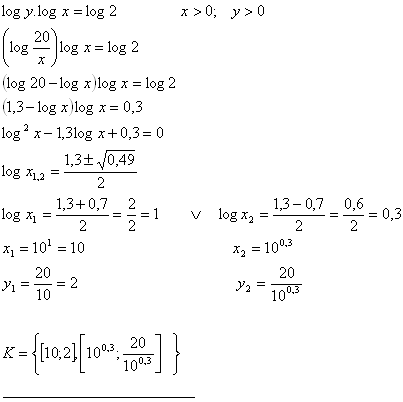
12. Solve the set of equations:
Solution:
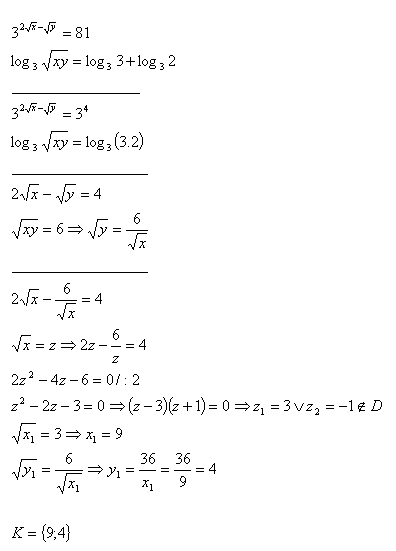
13. Solve the set of equations:
Solution:
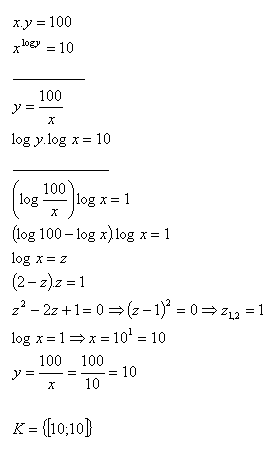
14. Solve the set of equations:
Solution:
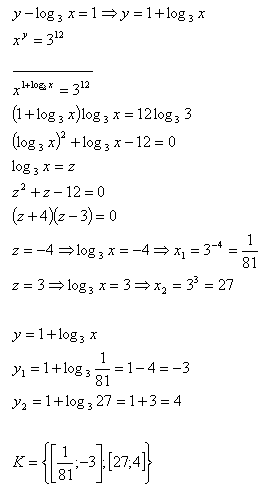
15. Solve the set of equations:
Solution:
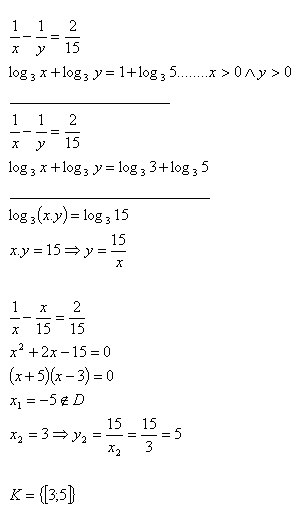
16. Solve the set of equations:
Solution:
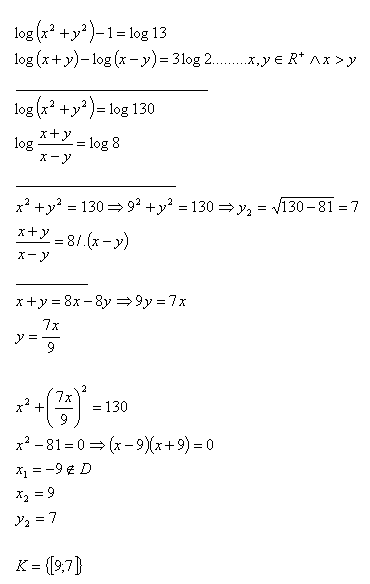
17. Solve the set of equations:
Solution:
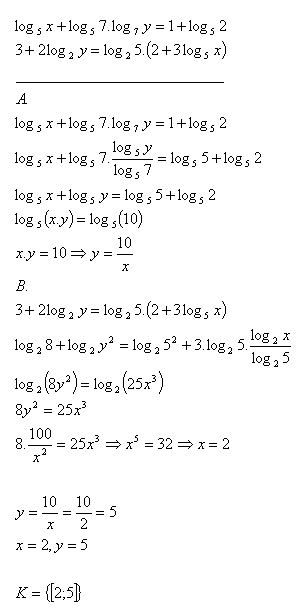
18. Solve the set of equations:
Solution:

19. Solve the set of equations:
Solution:
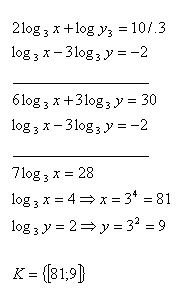
20. Solve the set of equations:
Solution: