Right Triangle

1. Define a right triangle.

Solution:


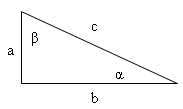
a) Pythagorean theorem:

a² + b² = c²

b) Goniometric functions:



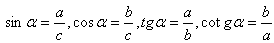
c) Perimeter:

O = a + b + c

d) Area:



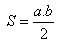
c) Euclid theorems:

a² = c.c_a
b² = c.c_b
v² = c_a.c_b

2. The catheti of a right triangle ΔABC are a =3 cm, b = 4 cm.

Solution:


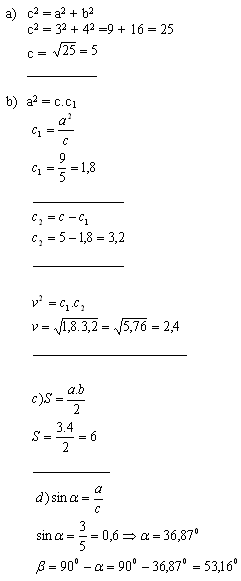
For the triangle ΔABC stands: c = 5cm, v_c = 2,4cm, S = 6cm², α = 36,87°, β = 53,16°.

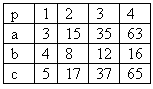
3. Let a, b be a right triangles‘ catheti, c a right triangles‘ hypotenuse, α the angle opposite to a.

Fill the table! (Lengths in cm)

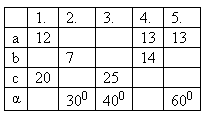
Solution:

4.The sides of a right triangle make an arithmetic progression. Determine:

5.Sum of the lengths of the catheti of a right triangle is 30 cm. The area of the triangle is 110,5 cm². Determine the perimeter of the triangle.

Solution:



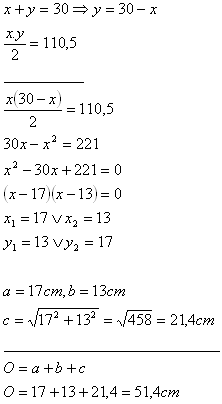
The perimeter of the triangle is 51,4 cm.

6. The leg of an isosceles triangle is 1 cm longer than it‘s base. The altitude is 2 cm shorter than the leg. Determine the size of the leg of the triangle.

Solution:


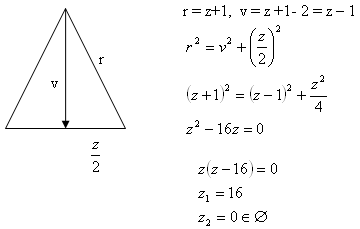
z = 16 cm, r = 17 cm, v = 15cm

7. A triangle‘s sides lengths equal a = 4p2- 1, b = 4p, c = 4p2+1. Prove that it‘s a right triangle and that it‘s a Pythagorean triangle. Write out four Pythagorean triangles.

Solution:

If a Pythagorean theorem stands for a triangle, it‘s a right triangle.

 

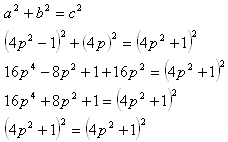
The triangle is a right triangle.

Pythagorean triangles:
 
Proof:
35² + 12² = 37²
1225 + 144 = 1369
1369 = 1369

8. Aké stúpanie má cesta, ak na dopravnej značke, ktorá o tom informuje, je napísané 6,7 %? Auto prešlo 2,3 km po tejto ceste.

Riešenie:


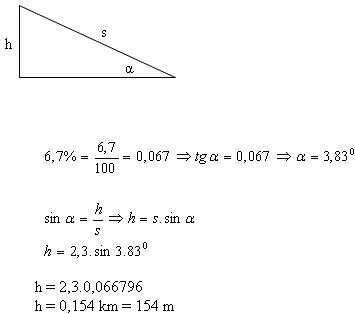
Uhol stúpania cesty je 3,83°.
Auto prekonalo výškový rozdiel asi 154 m.

9. Vypočítajte obsah rovnoramenného pravouhlého trojuholníka, ktorého obvod je 20cm.

Riešenie:

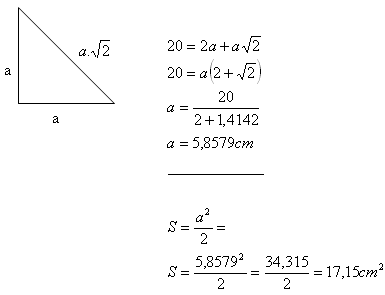
Obsah trojuholníka je 17,15 cm².

10. Pre odvesny pravouhlého trojuholníka platí a:b = 2:3. Prepona má dĺžku 10 cm.

Riešenie:





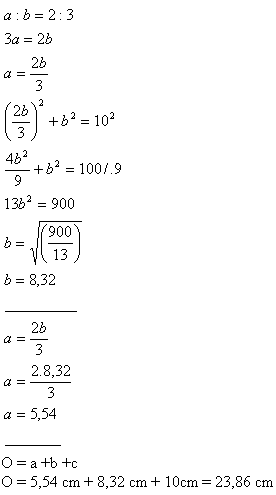
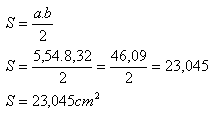
Obvod trojuholníka ΔABC je 23,86 cm a obsah 23,045 cm².