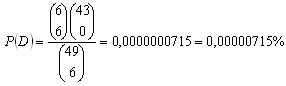Probability
1.Define and characterize probability.
Solution:
a)
Standard probability definition
Let a random event meet following conditions:
- number of the events is finite
- all events have the same chance to occur
- no two events can occur in the same time
Probability of an event A equals 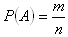 , n = # of all possible events, m = number of cases favorable for the event A
, n = # of all possible events, m = number of cases favorable for the event A
Stands: 0 ≤ P(A) ≤ 1
Probability of an impossible event : P(A) = 0
Probability of a sure event: P(A) = 1
b) Conditional probability of some event A, given the occurrence of some other event B:
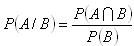
c) Probability of two independent events:
P(A∩B) = P(A)P(B)
d) Probability of two mutually exclusive events:
P(AUB) = P(A) + P(B)
e) Binomial probability expression:
Let an event A occur with probability P. The probability of k occurrances of the event A in n tries equals:
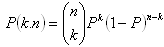
f) Hypergeometric probability expression:
Let V of N elements have a property p; derived from that, N-V elements do not have the property p.
Probability of k of n randomly selected elements having the property p equals::
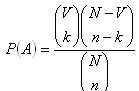
2.There are 18 tickets marked with numbers 1 to 18. What‘s the probability of selecting a ticket having the following property:
a) even number
b) number divisible by 3
c) prime number
d) number divisible by 6
Solution:
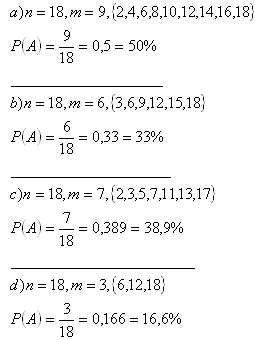
3.Determine the probability of following results when throwing 2 playing cubes (a red one and a blue one):
a) sum equals to 8
b) sum divisible by 5
c) even sum
Solution:
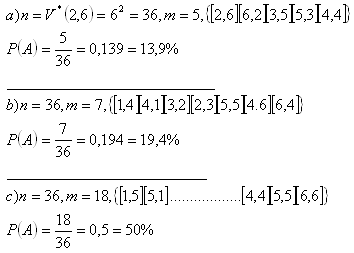
4.A gambler playing with 3 playing cubes wants to know weather to bet on sum 11 or 12. Which of the sums will occur more probably?
Solution:
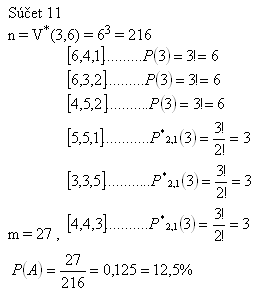
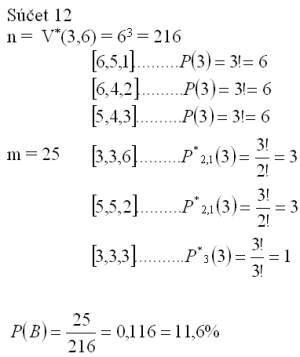
The gambler should bet on 11, as P(11) > P(12).
5.82 170 of 100 000 children live 40 years and 37 930 of 100 000 children live 70 years. Determine the probability of a 40 years old person to live 70 years.
Solution:
(Conditional probability)
A – live 70 years, P(A) = 0,3793
B – live 40 years, P(B) = 0,8217
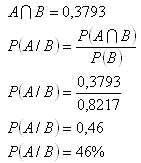
The probability equals 46%.
6.In a town there are 4 crossroads with trafic lights. Each trafic light opens or closes the traffic with the same probability of 0.5. Determine the probability of:
a) a car crossing the first crossroad without stopping
b) a car crossing first two crossroads without stopping
c) a car crossing all the crossroads (4) without stopping
Solution:
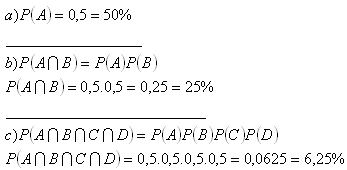
7.32 playing cards include 4 aces and 12 figures. Determine the probability of a randomly selected card to be an ace or a figure.
Solution:
Probability of two mutually exclusive events
A – selected ace 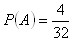
B - selected figure 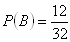
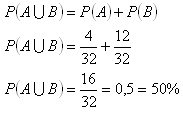
The probability of selecting an ace or a figure equals 50%.
8.Determine the probability of 3 of 5 born children being sons if the probability of a children to be a boy equals P(A) = 0,51.
Solution:
Binomial probability expression.
n = 5, k = 3, P = 0,51
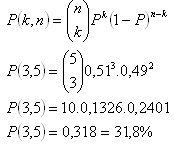
The probability equals 31,8 %.
9. There are 16 cola bottles on the table. 10 of them are filled by Coca Cola and 6 of them are filled by Pepsi. Determine the probability of 4 randomly selected bottles to include 2 Coca Cola and 2 Pepsi bottles.
Solution:
Hypogeometric probability expression.
N = 16 (# all bottles)
V = 10 (# Coca Cola)
N-V = 6 (# Pepsi)
n = 4 (# randomly selected bottles)
k = 2 (# selected Coca Cola)
n – k = 2 (# selected Pepsi)
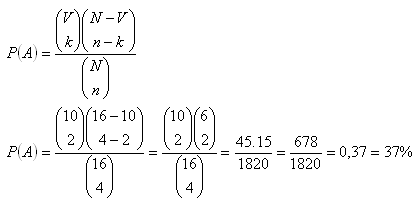
The probability equals P(A) = 37 %.
10.In a game of chance 6 of 49 numbers are the winning numbers. Determine the probability of reaching:
a) matching 3 of 6
b) matching 4 of 6
c) matching 5 of 6
d) matching 6 of 6
Solution:
a) Matching 3 of 6
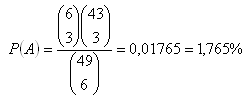
b) Matching 4 of 6
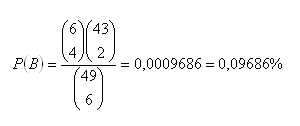
c) Matching 5 of 6
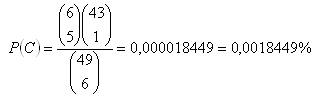
d) Matching 6 of 6