Logarithmic Equations
1. Solve:
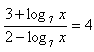
x > 0
Solution:
3+log7x = 8 – 4log7x
5log7x = 5
log7x = 1
x = 71 = 7
K = {7}
2. Solve:
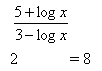
x > 0
Solution:
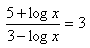
5+logx = 9-3logx
4logx = 4
logx = 1
x = 10
1= 10
K = {10}
3.Solve:
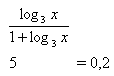
x > 0
Solution:
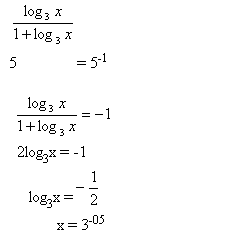
K = {3
-0,5}
4. Solve:
log3(5+4.log2(x-1)) = 2 x > 1
Solution:
log3(5+4.log2(x-1)) = 2
log3(5+4.log2(x-1)) = log39
5+4.log2(x-1) = 9
4.log2(x-1) = 4
log2(x-1) = 1
x-1 = 21
x = 3
K = {3}
5. Solve:
log(x+5) - log(x-1) = 1-log2 x > 1
Solution:
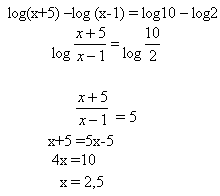
K = {2,5}
6. Solve:
log(x+2) + log(x-7) = 2.log(x-4) x > 7
Solution:
log(x+2) + log(x-7) = 2.log(x-4)
log (x+2)(x-7) = log(x-4)2
(x+2)(x-7) = (x-4)2
x2-5x-14 = x2-8x +16
3x = 30
x = 10
K = {10}
7. Solve:
log5x +log (2x + 3) = 1 + 2.log(3-x) x < 3
Solution:
log5x +log (2x + 3) = 1 + 2.log(3-x)
log5x + log(2x + 3) = log10 + log(3-x)
2
log(5x.(2x +3)) = log (10.(3-x)
2)
5x.(2x +3) = 10.(3-x)
2
10x
2 +15x = 10.(9-6x + x
2)
10x
2 + 15x = 90-60x +10x
2
75x = 90
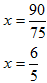
8. Solve:
log(1+x)–log(1-x) = log(x+3)-log(4-x) x < 1
Solution:
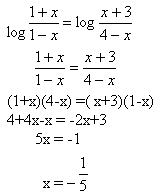
9. Solve:
2log3x2 + 3log4x3 = 4log2x2 +4log6x x > 0
Solution:
2log3x2 + 3log4x3 = 4log2x2 +4log6x
log9x4 + log64x9 = log16x8 + log1296x4
log(576x13) = log(20736x12)
576x13 = 20736x12/:576x12
x = 36
K = {36}
10.
Solve in real numbers:
Solution:
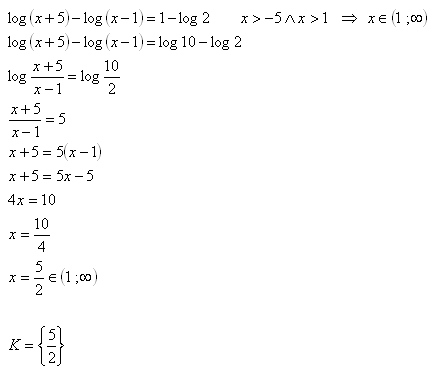
11.Solve in real numbers:
Solution:
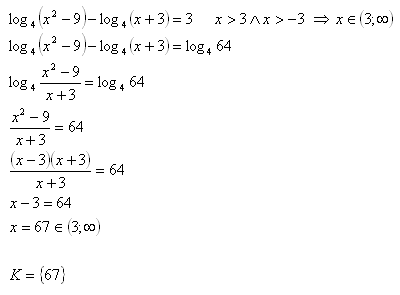
12.Solve in real numbers:
Solution:
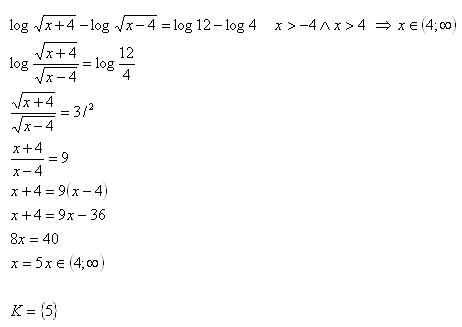
13.Solve in real numbers:
Solution:
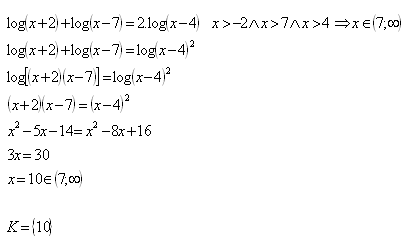
14.Solve in real numbers:
Solution:
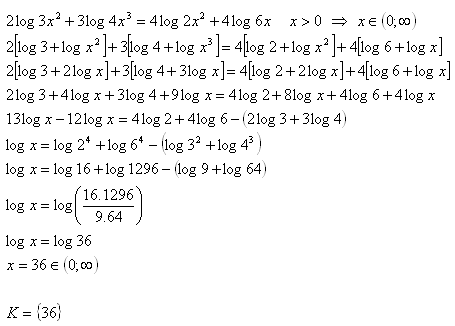
15.Solve in real numbers:
Solution:
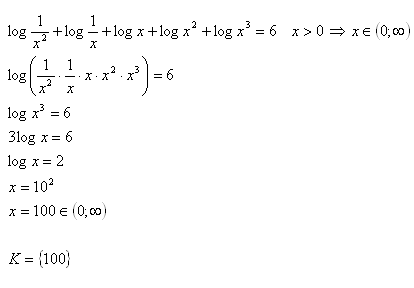
16.Solve in real numbers:
Solution:
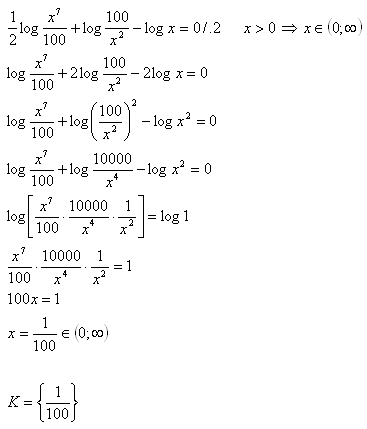
17.Solve in real numbers:
Solution:
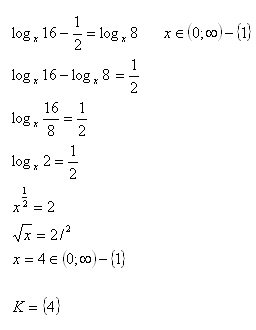
18.Solve in real numbers:
Solution:
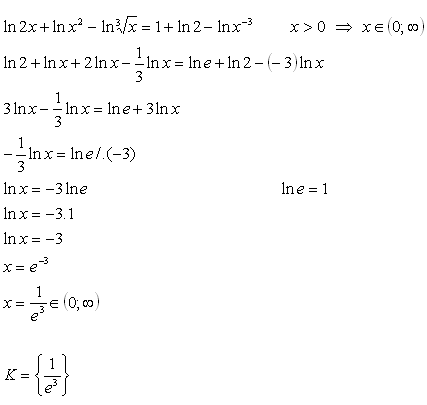
19.Solve in real numbers:
Solution:
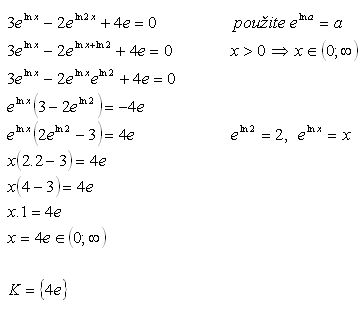
20.Solve in real numbers:
Solution:
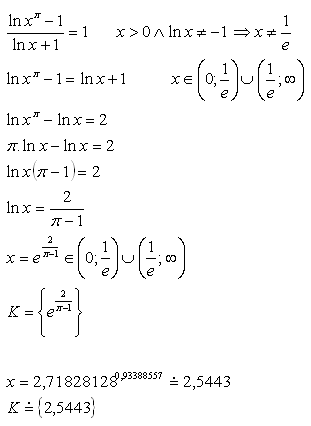
Logarithmic equations – further exercise: