Interesting facts
In this chapter you will find interesting and funny examples. To solve them you only need basic knowledge of chemistry, common sense, a calculator, and the desire to have fun.
1. Your social norm is 0.5 l of wine, which contains on average 12% v/v (9.6% w/v) alcohol. You join a group where only spirits are drunk. What will be the social norm for Whisky (40% v/v; 32% w/v)? Convert the final value into common servings – deci, half-deci, small, large.
Solution:
100 ml of wine contains, according to the task, 9.6 grams of pure alcohol. Therefore, 500 ml of wine will contain five times more, i.e., 9.6 x 5 = 48 grams of ethanol.
In 100 ml whisky...........32 g ethanol
In x ml whisky....….........48 g ethanol
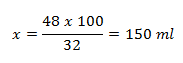
My social norm is therefore 1 large and 1 small Whisky.
2. A pensioner read that a limited amount of alcohol is beneficial to health. So he started drinking daily 0.3 l of Whisky (40% v/v; 32% w/v) and 1 l of beer (10% beer contains on average 3.2% w/v alcohol, resp. 4% v/v), but he started gaining weight...
- a) By how much must he reduce his food intake (calculated for a daily energy intake of 2000 Kcal) so that he does not gain weight?
- b) The daily dose that does not harm the liver in a healthy man is 60 g. In an 80-year-old retiree it can be estimated at 30 g. Is the amount of alcohol consumed safe for the liver? If not, calculate how many times it exceeds the safe dose.
- c) How much 10% beer can this retiree drink so that his liver is not damaged?
Note: Usable energy for ethanol – 7 Kcal per gram of alcohol
Solution:
a) The pensioner drank
300 ml Whisky, thus ingesting (3 x 32) = 96 grams of alcohol, which corresponds to (96 x 7) = 672 Kcal
1000 ml beer, i.e., (10 x 3.2 x 7) = 224 Kcal
Total 672 + 224 = 896 Kcal – that is approximately 1000 Kcal.
The pensioner must reduce food intake by about half.
b) The total amount of alcohol from Whisky and beer is (3 x 32 + 10 x 3.2) = 128 g alcohol.
x = 128/30 = 4.27
The pensioner consumes a dangerous amount of alcohol, which is 4.27 times above the safe dose.
c) The safe dose is 30 g alcohol per day, 100 ml beer contains 3.2 g alcohol. Therefore:
3.2 g ethanol ................100 ml beer
30 g ethanol ......……..........x ml beer
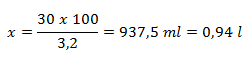
The pensioner can drink less than 2 large beers per day without liver damage.
3. How much 10% beer must a homeless person drink to cover his daily energy needs of 2000 Kcal? 10% beer contains on average 3.2% w/v alcohol (4% v/v) and about 3% residual maltose.
Usable energy for individual nutrients:
- 4 Kcal per gram of protein
- 4 Kcal per gram of carbohydrate
- 9 Kcal per gram of fat
- 7 Kcal per gram of alcohol
Solution:
100 ml beer contains 3.2 grams ethanol and 3 grams maltose. This equals (3.2 x 7 + 3 x 4) = 34.4 Kcal. The daily dose is 2000 Kcal, therefore
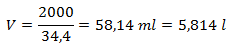
The homeless person must drink almost 12 large beers.
4.Approximately 70% of the human body is accessible to alcohol. Complete resorption of alcohol is achieved about 1 hour after consumption. What will be the blood alcohol concentration in a 70 kg man who drinks 0.5 l of 10% beer (contains 3.2% w/v; 4% v/v alcohol) after one hour?
Note: 1 beer 10% equals 0.33‰ for a 70 kg person
Solution:
1 beer equals 0.33‰, i.e., 3.3% (w/v), which corresponds to 3.3 g per 100 ml
The blood alcohol concentration will therefore be 3.3%.
5. The rate of ethanol breakdown in a healthy person is about 0.15‰ per hour. A drunk politician (80 kg) caused a car accident under the influence of alcohol. However, he claimed that he had drunk three deciliters of Orešanské wine (12% v/v; 9.6% w/v) an hour earlier. His blood alcohol level was measured at 1‰. Was he telling the truth? How much did he actually drink? (any similarity with real events is purely coincidental!)
Note: 1 deci of wine equals 0.2‰ in a 70 kg person
Solution:
After one hour the politician’s blood alcohol level was 1‰. If we add 0.15‰ that had already been metabolized in that hour, then:
100 ml..……..............0.2‰
x ml....................1.15‰
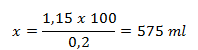
The politician must have drunk at least 6 deciliters of wine.