Molar mass

Solution:

The molar mass of molecular hydrogen (H₂) is 2.016 g·mol^-1. Substituting into the equation for calculating the mass per molecule gives:

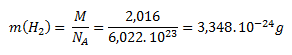
The molar mass of atomic hydrogen (H) is 1.008 g·mol^-1. The mass of a single hydrogen atom is calculated analogously to the molecule:

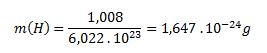
The mass of one hydrogen molecule is 3.348 × 10^-24 g and of one hydrogen atom is 1.647 × 10^-24 g.

Solution:

We start from the relation for molar mass. The molar mass of zinc from tables is 65.38 g·mol^-1.

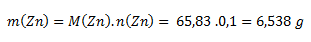
You need to weigh out 6.538 g of zinc.

Solution:

The given relative atomic mass of copper is the weighted average and its value depends on the percentage abundances of the two nuclides in the mixture. If we denote the percentage abundances as x and y, then the following equations apply:

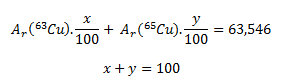
Because the numerical values of the atomic masses expressed in atomic mass units (u) are equal to the relative atomic masses, A_r(⁶³Cu) = 62.929 and A_r(⁶⁵Cu) = 64.928. Substituting these values into the equation gives:

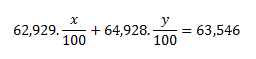
Substitute y = 100 − x

0.62929x + 0.64928(100 − x) = 63.546

Solving the equation gives the percentage abundance of nuclide ⁶³Cu:

x = 69.13%

Abundance of nuclide ⁶⁵Cu:

y = 100 − x = 100 − 69.13 = 30.87%

The mixture contains 69.13% of nuclide ⁶³Cu and 30.87% of nuclide ⁶⁵Cu.

Solution:

We start from the equations for amount of substance and molar mass.

The mother tincture contains in 1 liter salt with mass m₀ = 1 g; after the first dilution m₁ = 0.01m₀; after the second dilution m₂ = 0.01²m₀; and after the i-th dilution m_i = 0.01ⁱm₀. The number of NaCl “molecules” N_i after the i-th dilution is:

 ,

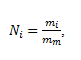where m_m is the mass of a “molecule” of NaCl. The term molecule is not strictly correct here, since due to the ionic nature of the bond between Na and Cl the compound is present in solution as ions.

After substitution:

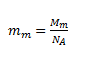
into the first equation we get:

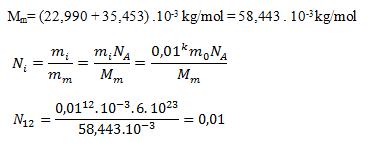
At the dilution level C12 there are 0.01 sodium cations per liter of water. In homeopathic treatment this is common—we are essentially taking a placebo without an active substance; any “effect” is psychological.

Solution:

The chemical equivalent of an element depends on the oxidation number of its atom in the compound. From the mass ratio of copper and oxygen we calculate the amounts of substance:

• copper

• oxygen

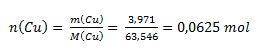
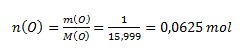
Since n(Cu) : n(O) = 1 : 1, the oxide has the composition CuO—copper(II) oxide. The Cu atom has oxidation number II and could thus bind two hydrogen atoms. One hydrogen atom corresponds to ½ atom of copper; therefore the chemical equivalent of copper in the oxide considered is ½ atom.

Solution:

Procedure as in example 2.

Result:  3.44 × 10^-22 g

Solution:

Procedure similar to example 3.

Result: 7.0142

Solution:

Multiply the atomic mass by Avogadro’s constant to obtain the mass of one mole of atoms, i.e., the molar mass of the element. The result is 190.21; from the periodic table we read that the element is Os (osmium). 

Solution:

The molar mass of water is 18 g/mol; for seven waters it is 7 × 18 = 126 g/mol. The molar mass of iron(II) sulfate heptahydrate is 277.909 g/mol.

In 277.909 g of iron(II) sulfate heptahydrate ................ 126 g of crystallization water

In 50.4 g of heptahydrate ................................................................. x g of water

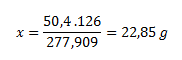
From that we calculate the amount of substance:    

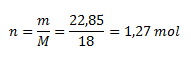
The amount of water in iron(II) sulfate heptahydrate is 1.27 mol.

Solution:

• a) 8.83 mmol
• b) 0.249 mol
• c) 0.581 mol