Atomic nucleus

1. What properties does the atomic nucleus have?

Solution:
The atomic nucleus forms the central part of the atom. It accounts for almost all of its mass. The atomic nucleus contains protons and neutrons—nucleons.

Atomic constant: $m_u, A_r = 1, m = 1.6605 \cdot 10^{-27} \, \text{kg} = 931.5 \, \text{MeV} \cdot c^{-2}$

Proton: $p, A_{r} = 1.0072, m = 1.673 \cdot 10^{- 27} kg = 938.275 MeV \cdot c^{- 2}$
Neutron: $n, A_{r} = 1.0086, m = 1.673 \cdot 10^{- 27} kg = 939.565 MeV \cdot c^{- 2}$

$^A_Z X$ $, Z =$ proton number (number of protons in the nucleus, electrons in the shell, the order of the element in the Mendeleev table)
$N =$ neutron number (number of neutrons in the nucleus)
$A =$ nucleon number $A = N + Z$ (number of nucleons – protons and neutrons in the nucleus)

Isotopes are nuclides of the same element (same $Z$ ) that differ in neutron number $N$ (and thus also in number $A$ ).

The mass of the nucleus $m_j$ is always smaller than the mass of $Z$ protons and $N$ neutrons.

$B_j =$ mass defect of the nucleus:

$m_j < Z \cdot m_p + N \cdot m_n$ $m_j + B_j = Z \cdot m_p + N \cdot m_n$ $B_j = (Z \cdot m_p + N \cdot m_n) - m_j$

$m_j = A_r \cdot m_u$

Binding energy of the nucleus:

E_j = B_j c^2

Binding energy per nucleon:

\varepsilon_j = \frac{E_j}{A}

New unit of mass:

$1 \, \text{MeV} \cdot c^{-2} = 1.7825 \cdot 10^{-30} \, \text{kg}$

$1 \, \text{kg} = 0.561 \cdot 10^{30} \, \text{MeV} \cdot c^{-2}$

2.Lead has four isotopes. Determine the number of protons and neutrons in the nucleus.

Solution:

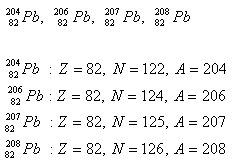
3. Calculate:

a.) the rest mass of the nitrogen nucleus, given A_r(N) = 14,0067
b.) the relative mass of the chlorine nucleus, given m(Cl) = 5,885·10^–26 kg, 1 MeV·c^–2 = 1,7825·10^–30 kg, m_u = 1,6605·10^–27 kg

Solution:

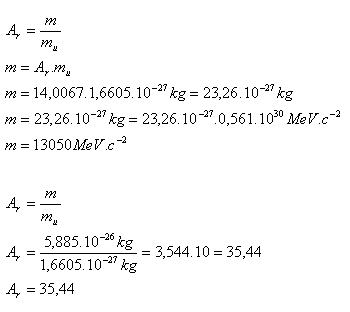
The rest mass of the nitrogen nucleus is m = 13 050 MeV·c^-2.
The relative mass of the chlorine nucleus is A_r = 35.44.

4.Determine the mass defect, the binding energy, and the energy per nucleon for a radium nucleus. Express the energy in MeV.

Solution:

Analysis:

The mass defect is B_j = 1708.9 MeV·c^-2, the binding energy is E_j = 1708.9 MeV, the energy per nucleon is ε_j = 7.56 MeV.

5.Determine the percent composition of chlorine with a relative atomic mass of 35.5, which is a mixture of isotopes

Solution:

Analysis:

x = relative abundance of the first isotope
y = relative abundance of the second isotope

35x + 37y = 35.5

x + y = 1 \quad \Rightarrow \quad y = 1 - x

35x + 37(1 - x) = 35.5

35x + 37 - 37x = 35.5

-2x = -1.5

2x = 1.5

x = 75\% \quad (= 0.75)

y = 25\% \quad (= 0.25)

Chlorine contains 75% of the first isotope and 25% of the second isotope.

6.In the atomic bomb dropped by the Americans on Hiroshima, the charge contained 44.5 kg of uranium. What energy was released?

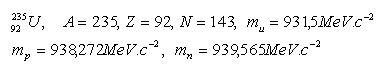
Solution:

$23592 U$ $A = 235, Z = 92, N = 143, m_{u} = 931.5 MeV c^{- 2}$

$m_p = 938.272\,\text{MeV}\,c^{-2},\quad m_n = 939.565\,\text{MeV}\,c^{-2}$

B_j = (Z\,m_p + N\,m_n) - A\,m_u

B_j = (92\cdot 938.272\,\text{MeV}\,c^{-2} + 143\cdot 939.565\,\text{MeV}\,c^{-2}) - 235\cdot 931.5\,\text{MeV}\,c^{-2} = 1776\,\text{MeV}\,c^{-2}

B_j = 1776\,\text{MeV}\,c^{-2}

Energy of one nucleon:

E_j = B_j\,c^2

E_j = 1776\,\text{MeV}\,c^{-2}\cdot c^2 = 1776\,\text{MeV}

E_j = 1776\,\text{MeV} = 2.84\times 10^{-10}\,\text{J}

Mass of the nucleus:

m = A\,m_u = 235\cdot 931.5\,\text{MeV}\,c^{-2} = 218902.5\,\text{MeV}\,c^{-2} = 3.9\times 10^{-25}\,\text{kg}

Number of nuclei in 1 kg:

n = \frac{1\,\text{kg}}{3.9\times 10^{-25}\,\text{kg}} = 2.56\times 10^{24}\ \text{nuclei}

Number of nuclei in 44.5 kg of uranium:

N = 44.5\cdot 2.56\times 10^{24} = 1.14\times 10^{26}\ \text{nuclei}

Total energy:

E = N\,E_j = 1.14\times 10^{26}\cdot 2.84\times 10^{-10}\,\text{J} = 3.24\times 10^{16}\,\text{J}

E = 3.24\times 10^{16}\,\text{J}

Total energy is: $E = 3.24 \times 10^{16}$

7.How long would it take a power plant, whose two blocks have a power output of P = 2,440 MW, to produce the energy from problem no. 6 (E = 3.24·10¹⁶ J)?

Solution:

Analysis:

E = 3.24·10¹⁶ J, P = 2,440 MW = 880·10⁶ J·s^-1, t = ?

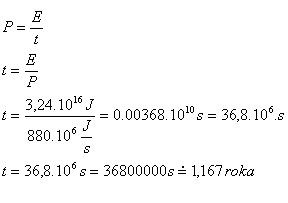
The power plant would produce this energy in 1.167 years.

8.A nucleus with mass number 100 and binding energy ε_j1 = 7.4 MeV splits into two nuclei with binding energy per nucleon ε_j2 = 8.2 MeV. What energy is released in the reaction?

Solution:

Analysis:

A = 100, ε_j1 = 7.4 MeV, ε_j2 = 8.2 MeV, E_j = ?

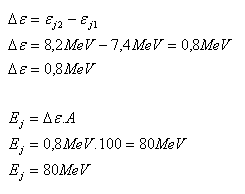
The reaction releases 80 MeV of energy.

9. Determine the energy obtainable by fission of 1 kg of uranium 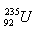if fission of one uranium nucleus releases 200 MeV of energy. What mass of hard coal with a heating value of 3·10⁷ J·kg would be needed to obtain the same energy?

Solution:

The mass of hard coal would need to be M = 2,733 tons.

10.A block of a nuclear power plant that converts nuclear energy into electrical energy with 40% efficiency has an electrical output of 600 MW. Determine the mass of uranium 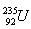consumed in 24 hours if fission of a single nucleus releases energy of 200 MeV.

Solution:

Analysis:

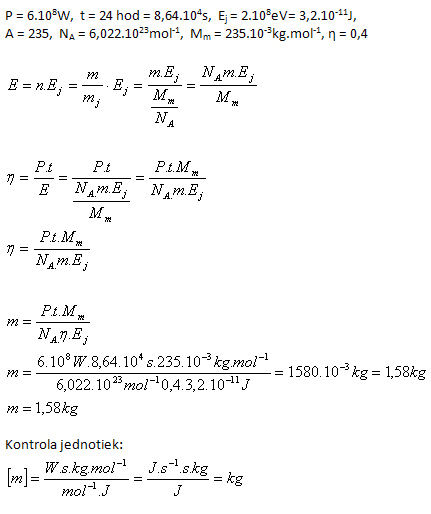
The mass of uranium is 1.58 kg.

11.Show that for the units of mass used in atomic physics, the following holds:

Solution:

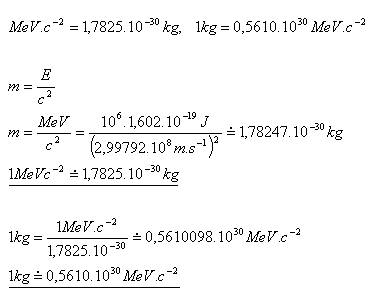
atomove-jadro-11

12.Express, in units of MeV c^–2, the mass of the atomic mass constant m_u, the proton m_p, and the neutron m_n.

Solution:

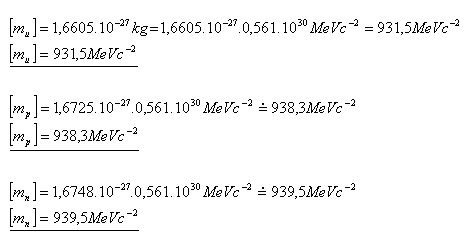
atomove-jadro-12

The mass of the atomic mass constant is m_u = 931.5 MeV c^–2,
the proton m_p = 938.3 MeV c^–2, and the neutron m_n = 939.5 MeV c^–2.

13.Determine the binding energy of the carbon nucleus per nucleon.

Solution:

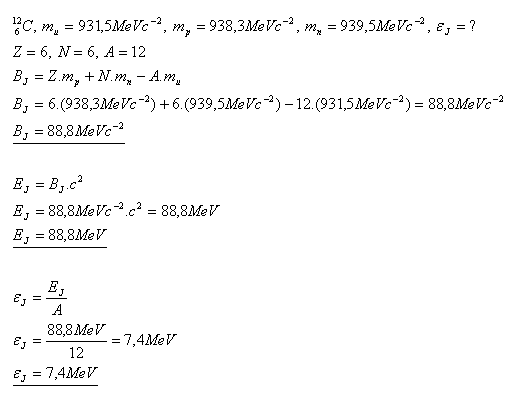
atomove-jadro-13

The binding energy of the carbon nucleus per nucleon is ε = 7.4 MeV.

14.Determine the number of uranium atoms in 1 kg of uranium.

Solution:

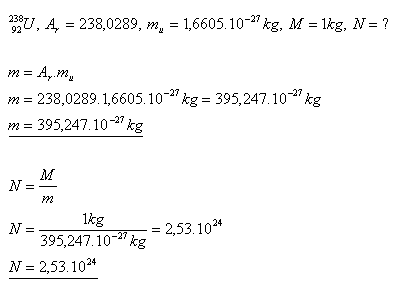
atomove-jadro-14

In 1 kilogram of uranium there are N = 2.53×10²⁴ uranium atoms.

15.Find how many protons and how many neutrons are in 1 kg of neon.

Solution:

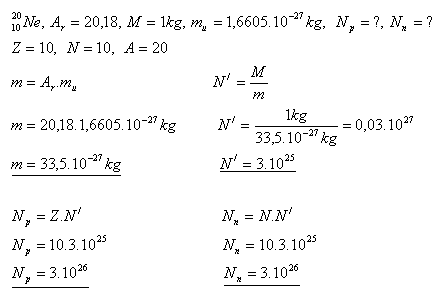
atomove-jadro-15

In one kilogram of neon there are 3×10²⁶ protons and 3×10²⁶ neutrons.

16.Determine the total binding energy of nuclei in one kilogram of uranium. One kilogram of uranium contains 2.53×10²⁴ atoms.

Solution:

atomove-jadro-16

The total binding energy of uranium nuclei is E = 7.3×10¹⁴ J.

17.Calculate the magnitude of the electric force

a.) by which two protons in a nucleus repel each other (r = 10^–15 m)
b.) by which a proton and an electron attract each other (r = 10^–10 m)

Solution:

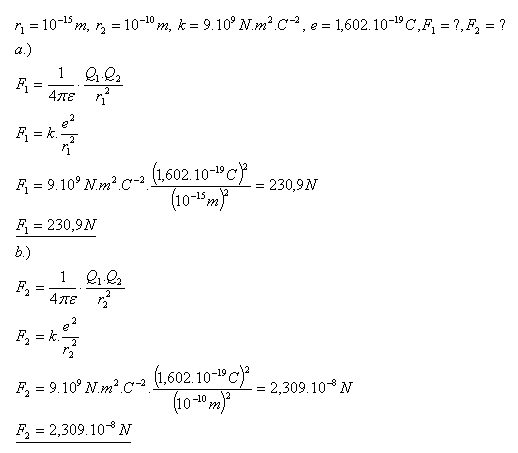
atomove-jadro-17

The forces are F₁ = 230.9 N and F₂ = 2.309×10^–8 N.

18.A nucleus with mass number A = 230 and binding energy per nucleon
ε_j1 = 7.4 MeV splits into two nuclei with binding energy per nucleon ε_j2 = 8.3 MeV. What energy is released during fission?

Solution:

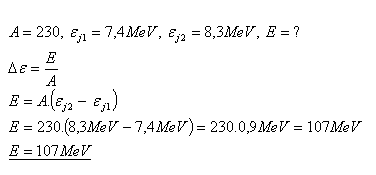
atomove-jadro-18

During fission, energy E = 107 MeV is released.

19.Boron, as it occurs in nature, is a mixture of two isotopes. The average atomic mass of boron is 10.82 m_u. What percentage of each isotope is in natural boron if:

Solution:

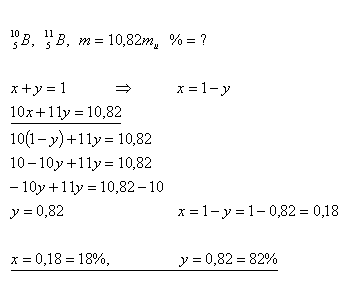
atomove-jadro-19r

Natural boron contains 18% of the first isotope and 82% of the second isotope.

20.Compare the density of the hydrogen nucleus with the density of water.

Solution:

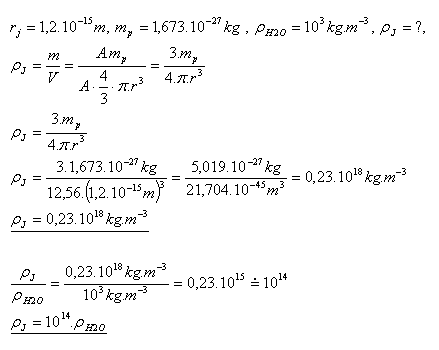
atomove-jadro-20

The density of the hydrogen nucleus is about 10¹⁴ times greater than the density of water.

Physics

Atomic nucleus

Adblock detected