Motions in a radial gravitational field
1. Characterize Earth's radial gravitational field.
Solution:
If the trajectory of a mass point moving in Earth's gravitational field is comparable with the dimensions of Earth, the gravitational field is radial. A radial gravitational field is spatially unbounded. At different places in such a field the gravitational acceleration has different directions, because it always points toward the center of the Earth, and different magnitudes, which depend on the distance of the given place from the Earth's center. Examples of motion in Earth's radial gravitational field are the motions of artificial Earth satellites, the trajectories of intercontinental missiles and rockets, etc.
A body of mass m moving in Earth's gravitational field is acted on by
a) centrifugal force:
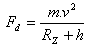
b) gravitational force:
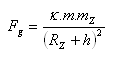
The body has
a) kinetic energy:
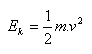
b) potential energy:
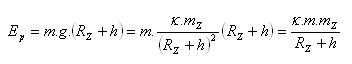
The three Kepler laws apply to the Sun's radial gravitational field:
1.) Planets move around the Sun on ellipses slightly different from circles; the Sun is at one focus.
2.) The areas swept out by the radius vector of a planet in equal times are equal.
3.)
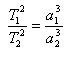
T
1, T
2 are the orbital periods of two planets, and a
1, a
2 are the semi-major axes of their trajectories.
2.Calculate the first and second cosmic velocities.
Solution:
- a.) First cosmic velocity v1
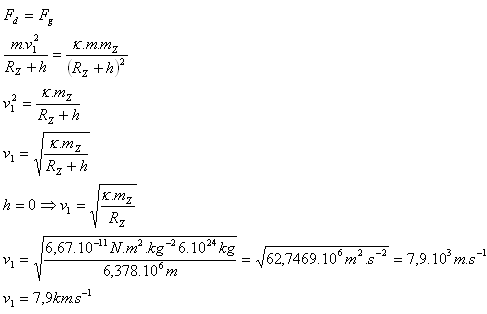
- b.) Second cosmic velocity v2
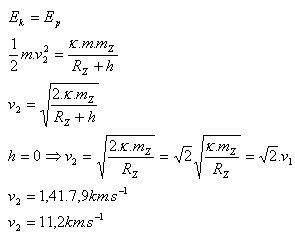
- The first cosmic velocity (circular) is v1 = 7.9 km·s-1.
- The second cosmic velocity (parabolic, escape) is v2 = 11.2 km·s-1. The body permanently moves away from Earth but remains in the Sun's gravitational field.
- The third cosmic velocity is v3 = 16.7 km·s-1. The body leaves the Sun's gravitational field.
3. At a certain time two satellites were observed from Earth at different altitudes (h1 = RZ, h2 = 2RZ), moving on circular trajectories in the same direction. Determine their speeds. v1 = 7.9 km·s-1
Solution:
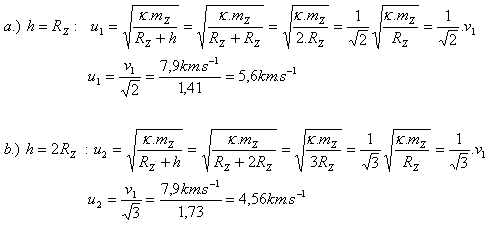
The satellite speeds are u1 = 5.6 km·s-1 and u2 = 4.56 km·s-1.
4.Determine the parabolic (second cosmic) velocity at the surface of the Moon. mM=7.41·1022 kg, RM=1.736·106 m
Solution:
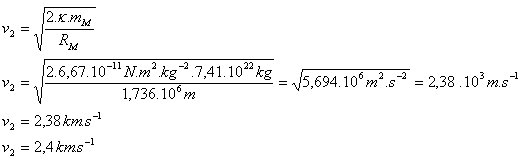
The second cosmic velocity at the Moon's surface is v2 = 2.4 km·s-1.
5. The mass of the Sun is mS = 1.989·1030 kg. The Earth's orbital speed around the Sun is v = 29.82 km·s-1. At what distance does the Earth orbit the Sun?
Solution:
Analysis:
mS = 1.989·1030 kg, v = 29.82 km·s-1 = 29.82·103 m·s-1
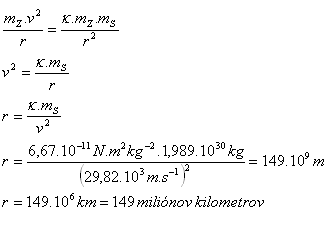
r (exact) = 149 597 900 km
A rounded value AU = 150·106 km may be used. This is the “astronomical unit”.
6.The Moon orbits the Earth at a distance of 384 000 km and has a mass of 7.41·1022 kg. On the line connecting the centers of the two bodies find the point C where a person would be weightless. At this point Earth's gravitational force equals the Moon's gravitational force.
Solution:
Analysis:
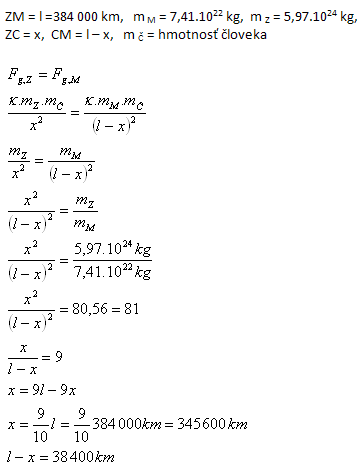
The sought point C (libration, Lagrange point) is at a distance of 345 600 km from Earth and 38 400 km from the Moon.
7.The largest planet in the Solar System, Jupiter, orbits the Sun at a distance of 7.8·108 km. The mass of the Sun is 1.989·1030 kg. What is the mass of Jupiter if the Sun attracts it with a gravitational force Fg= 4.2·1023 N? What acceleration does the Sun give Jupiter? What is Jupiter's orbital period T around the Sun?
Solution:

The mass of Jupiter is 1.9·1027 kg, its acceleration is 2.2·10-4 m·s-2. Jupiter's orbital period around the Sun is 11.8 (Earth) years.
8.At what height h above Earth must a geostationary satellite be placed so that it remains above the same spot on Earth's surface?
Solution:
Analysis:
mZ = 6·1024 kg, RZ = 6.378·106 m, TZ = 23 h 56 min 4 s = 8.6164·104 s
mD = mass of the satellite
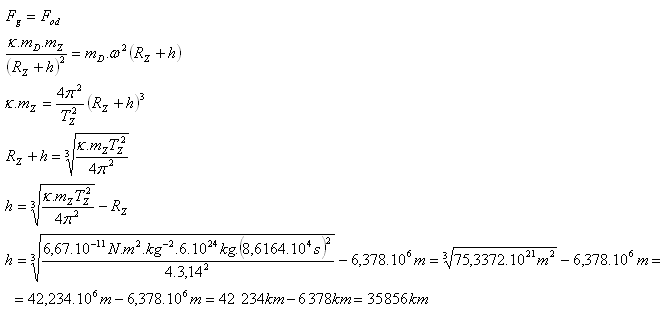
A geostationary satellite must be placed at a height of 35 856 km above Earth.
9. Using Kepler's laws determine:
- a.) What is the mean distance of the planet Venus from the Sun if its orbital period is TV=0.615 year.
- b.) What is the orbital period of Mercury around the Sun if its mean distance from the Sun is aM = 0.387 AU
Solution:

- The distance of Venus from the Sun is approximately 108.5·106 km.
- The orbital period of Mercury around the Sun is approximately 88 days.
10.A spacecraft launches from a geostationary orbital station located at height h = 35 856 km above Earth (see example no. 8) toward the Moon. How long does it take the spacecraft to reach the Moon's vicinity?
Solution:
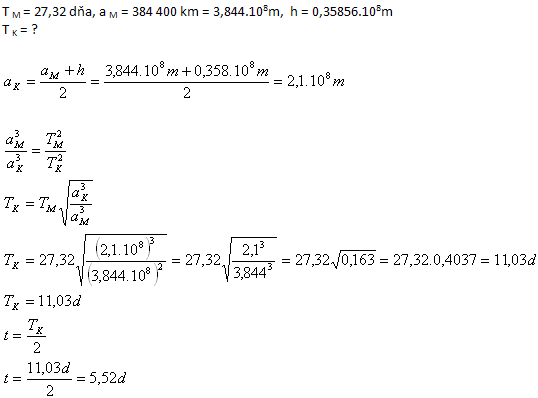
The period of the entire spacecraft trajectory is 11.03 days. The trip from Earth to the Moon takes half of this period, i.e. about 5.52 days.