Energy
1.Briefly characterize the physical quantity energy.
Solution:
Energy is the ability of bodies to do work.
Energy:
- 1.) kinetic (motion) energy Ek
- 2.) potential (position) energy Ep
1.) Kinetic energy. Every body that is in motion has kinetic energy.
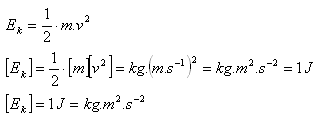
2.) Gravitational potential energy. Every body that is at a certain height above the Earth has potential energy.
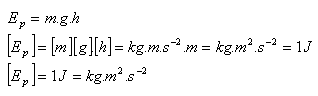
Law of conservation of mechanical energy:
In the isolated system body–Earth, the total mechanical energy is constant. At any moment, the sum of kinetic and potential energy is constant.
E = Ek + Ep = const.
2.A Ford Fusion car with a mass of 1156 kg increased its speed from 18 km·h-1 to 72 km·h-1. By how much did its kinetic energy increase?
Solution:
Given:
m = 1156 kg, v1 = 18 km·h-1 = 5 m·s-1, v2 = 72 km·h-1 = 20 m·s-1
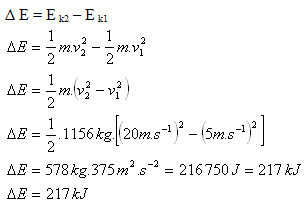
The car’s kinetic energy increased by ΔE = 217 kJ.
3.In what ratio are the kinetic energies of two balls if the second has twice the mass and four times the speed of the first?
Solution:
Given:
m2 = 2·m1, v2 = 4·v1
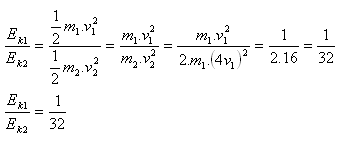
The kinetic energies are in the ratio 1 : 32.
4. A boat moves across a lake at a speed of 36 km·h-1. On deck a sailor of mass 80 kg walks at a speed of 2 m·s-1. Calculate his kinetic energy with respect to the lake if he walks
- a.) in the direction of travel
- b.) against the direction of travel
Solution:
Given:
m = 80 kg, v1 = 36 km·h-1 = 10 m·s-1, v2 = 2 m·s-1
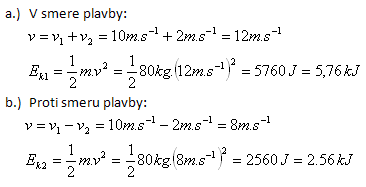
The sailor’s kinetic energy is
- a.) 5.76 kJ,
- b.) 2.56 kJ.
5.A train with a mass of 200 tons moves at a speed of 54 km·h-1. When stopping, the brakes exert a force which, recalculated per each 1000 kg of the train’s mass, is 300 N. Determine:
- a.) the train’s kinetic energy before braking
- b.) the work the brakes must do to stop the train
Solution:
Given:
m = 200 t = 2·105 kg, v = 54 km·h-1 = 15 m·s-1,
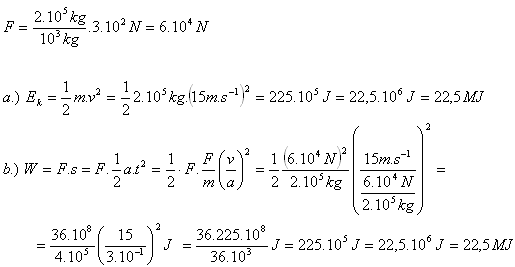
The work the brakes must do to stop the train equals the train’s kinetic energy before braking.
Ek = W = 22.5 MJ.
6.A weight of mass 2 kg is at a height of 50 cm above the surface of a table. The tabletop is 1.5 m above the room floor. Determine the potential energy of the weight
- a.) with respect to the tabletop
- b.) with respect to the room floor
Solution:
- a.) With respect to the tabletop
m = 2 kg, h1 = 0.5 m, g = 10 m·s-2
Ep1 = m·g·h1 = 2 kg·0.5 m·10 m·s-2 = 10 kg·m2·s-2 = 10 J
Ep1 = 10 J
- b.) With respect to the room floor
m = 2 kg, h2 = 0.5 m + 1.5 m = 2 m, g = 10 m·s-2
Ep2 = m·g·h2 = 2 kg·2 m·10 m·s-2 = 40 kg·m2·s-2 = 40 J
Ep2 = 40 J
The potential energy of the weight with respect to the tabletop is 10 J; with respect to the room floor it is 40 J.
7.A ram of mass 400 kg falls from a height of 3 m. On impact it drives a stake to a depth of 60 cm. What is the magnitude of the average force overcoming the resistance of the soil?
Solution:
Given:
m = 400 kg, h = 3 m, s = 60 cm = 0.6 m, g = 10 m·s-2, F = ?
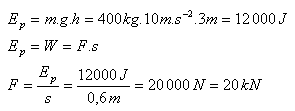
The average force overcoming the soil resistance is F = 20 kN.
8.From a tower 45 m high, a stone of mass 300 g falls freely. Determine the total mechanical energy of the stone with respect to the Earth at the end of the first second of motion.
Solution:
Given:
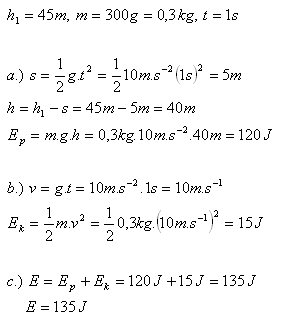
The total mechanical energy of the stone is E = 135 J.
9.Alpha particles are emitted during the radioactive decay of elements. They have a mass of 6.6·10-27 kg and a speed of 2·104 km·s-1. How many alpha particles will perform 1 J of work when braking in so-called “heavy water”?
Solution:
Given:
m = 6.6·10-27 kg, v = 2·104 km·s-1 = 2·107 m·s-1, W = 1 J
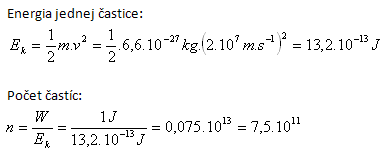
The required work is performed by 7.5·1011 particles.
10. A mountain hut was damaged by a stone of mass 120 kg that originally hung 20 m above the hut. With what speed did the stone hit the hut? What would this speed be if the stone had a mass of 60 kg?
Solution:
Given:
m = 120 kg, h = 20 m
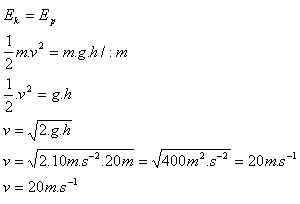
The stone hit the hut with speed v = 20 m·s-1.
The speed of free fall does not depend on the mass of the falling body.
11.A ball of mass 200 g swings on a thin thread. As it passes the lowest position it has a speed of 3 m·s-1. What maximum height will the ball reach when displaced?
Solution:
Given:
m = 200 g = 0.2 kg, v = 3 m·s-1, g = 10 m·s-2
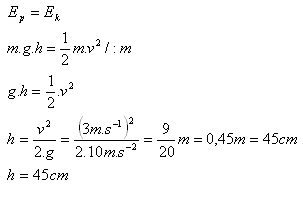
The ball rises to a maximum height h = 45 cm.
12. A body of mass 2 kg is thrown vertically upward. At a height of 15 m it has kinetic energy 450 J. To what maximum height will the body rise?
Solution:
Given:
m = 2 kg, Ek15 = 450 J, h15 = 15 m
a.) Total energy of the body at height h
15 = 15 m:
E15 = Ek15 + Ep15 = Ek15 + m·g·h15 = 450 J + 2 kg·10 m·s-2·15 m = 450 J + 300 J = 750 J
b.) Total energy of the body at the maximum height h:
Emax = 750 J, Ek = 0
Emax = Ek + Ep
Emax = 0 + m·g·h
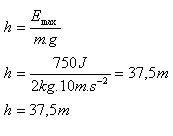
The body will rise to a maximum height h = 37.5 m.
13. A bullet of mass 6 g moving at a speed of 350 m·s-1 pierced a wooden board 20 cm thick and exited it with a speed of 150 m·s-1. Determine the mean value of the force with which the bullet acted on the board.
Solution:
Given:
m = 6 g = 0.006 kg, s = 20 cm = 0.2 m, v1 = 350 m·s-1, v2 = 150 m·s-1
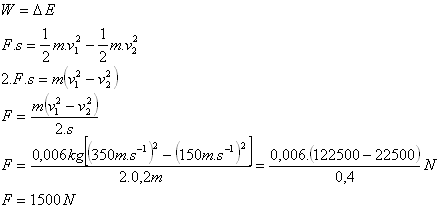
The bullet acted on the board with a force F = 1500 N.
14. A cart of mass 250 kg moves on horizontal rails at 2.4 m·s-1 and collides with an identical cart moving at 1.8 m·s-1. After the collision the carts stick together and continue moving jointly. Calculate what part of the mechanical energy is converted into other forms if the carts before the collision are moving
- a.) one behind the other
- b.) toward each other
Solution:
Given:
m1 = 250 kg, v1 = 2.4 m·s-1, m2 = 250 kg, v2 = 1.8 m·s-1
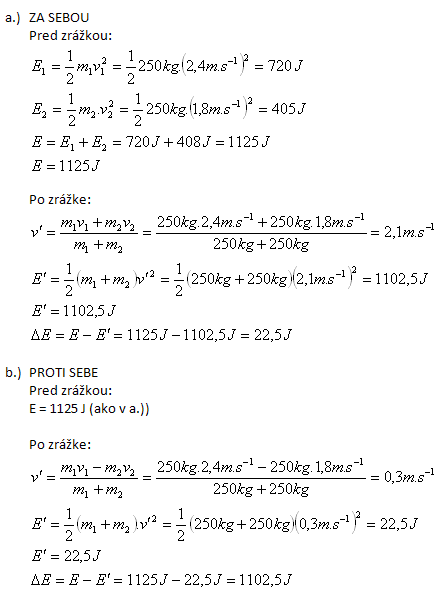
Converted into other forms of energy:
- a.) ΔE = 22.5 J
- b.) ΔE = 1102.5 J
15.A railway wagon with a mass of 10 Mg hit a rigid buffer at a speed of 4 m·s-1. By what length is the wagon’s buffer spring compressed if its stiffness is 4 MN·m-1? (This uses elastic potential energy Ep = 1/2·k·y2, where k = spring stiffness, y = extension or compression of the spring.)
Solution:
Given:
m = 10 Mg = 107 g = 104 kg, k = 4 MN·m-1, v = 4 m·s-1
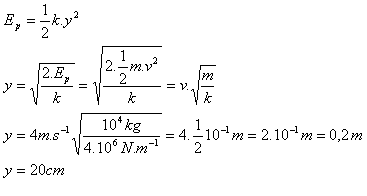
The spring is compressed by 20 cm.