sk|cz|de|

Mathematics

Pyramid and Cone


1. Characterize the calculation of volume and surface area for:

  • pyramid
  • truncated pyramid
  • cone
  • truncated cone

Solution:  

Pyramid (Sₚ = base, v = height, Q = lateral surface area)

V=13Sp⋅v,S=Sp+QV = \frac{1}{3} Sₚ \cdot v, \quad S = Sₚ + Q

Truncated pyramid (Sₚ₁, Sₚ₂ = lower and upper base, v = height, Q = lateral surface area)

V=13v(Sp1+Sp2)2,S=Sp1+Sp2+QV = \frac{1}{3} v ( \sqrt{Sₚ₁} + \sqrt{Sₚ₂})^2, \quad S = Sₚ₁ + Sₚ₂ + Q

Cone (r = base radius, v = height of the solid, s = slant height, Q = lateral surface area)

V=13πr2v,S=πr(r+s),Q=πrsV = \frac{1}{3} \pi r^2 v, \quad S = \pi r (r + s), \quad Q = \pi r s

Truncated cone (r₁, r₂ = radii of the bases, v = height of the solid, s = slant height)

V=13πv(r12+r1r2+r22),S=π(r12+r22)+Q,Q=πs(r1+r2)V = \frac{1}{3} \pi v (r₁^2 + r₁ r₂ + r₂^2), \quad S = \pi (r₁^2 + r₂^2) + Q, \quad Q = \pi s (r₁ + r₂)

2. A regular square pyramid is given (the base is a square with side a).

Fill in the missing values of the table.

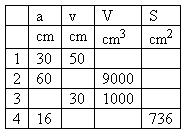
pyramid-cone-2

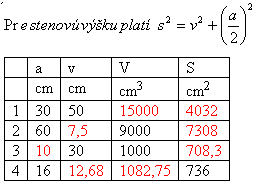
Solution:

For wall height apply:
pyramid-cone-2r

3. Above each face of a cube with edge a = 30 cm, a regular square pyramid with height 15 cm is constructed.

Calculate the volume of the solid formed in this way, if the vertices of the pyramids:
a) lie outside the cube
b) lie inside the cube
Solution:

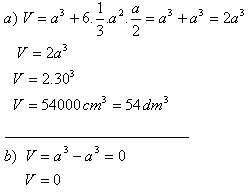
pyramid-cone-3

The volume of the solid in the first case is V = 54 dm3, in the second case it is zero.

4. Calculate the volume of a pyramid whose lateral edge of length 5 cm forms an angle α = 60° with the square base. (Angle α is the angle between the edge and the diagonal of the base.)

Solution:
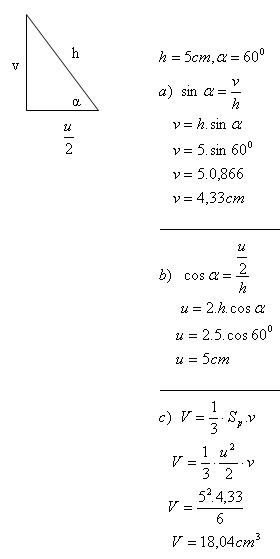
pyramid-cone-4

The volume of the pyramid is V = 18.04 cm3.

5. Determine the mass of a concrete pillar (ρ = 2.2 g.cm-3) in the shape of a regular square frustum of a pyramid, if its square bases have sides a = 45 cm, b = 25 cm, and the height of the pillar is v = 33 cm.

Solution:

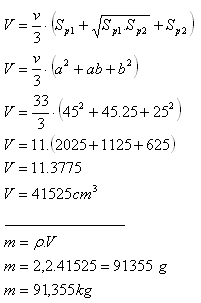
pyramid-cone-5

The mass of the concrete pillar is m = 91.355 kg.

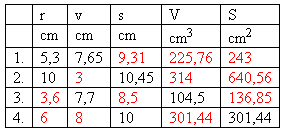
6. A cone with dimensions given in the table is given.

Fill in the table.

pyramid-cone-6
Solution:

pyramid-cone-6r

7. A right triangle with legs a = 3 cm, b = 4 cm rotates around the longer leg.

Calculate the volume and surface area of the cone formed.
Solution:
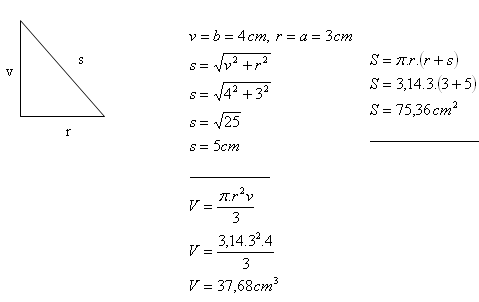
pyramid-cone-7

The cone has volume V = 37.68 cm3 and surface area S = 75.36 cm2.

8. The surface area of a cone is S = 235.5 cm2. The axial section of the cone is an equilateral triangle.

Calculate the volume of the cone.
Solution:

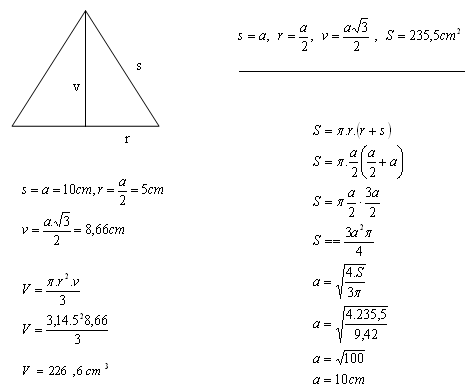
pyramid-cone-8

The volume of the cone is 226.6 cm3.

9. The lateral surface of a cone, developed into the plane, has the shape of a circular sector with central angle α = 150° and area S = 523.4 cm2.

Calculate the dimensions of this cone and its volume.
Solution:

S = 523.4 cm2 – area of the circular sector with radius R – lateral surface area with radius r
o = R · arcα – circular arc corresponding to the sector
O = 2πr – circumference of the base circle of the cone

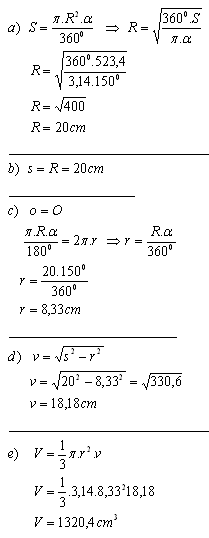
pyramid-cone-9

The dimensions of the cone are r = 8.33 cm, s = 20 cm, v = 18.18 cm and volume V = 1320.4 cm3.

10. The surface area of a frustum of a cone is 7693 cm2, the radii of the bases are 28 cm and 21 cm.

Calculate the height of the cone and its volume.
Solution:

S = 7693 cm2
R = 28 cm
r = 21 cm

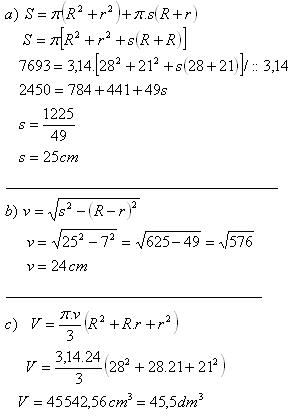
pyramid-cone-10

The height of the cone is v = 24 cm, its volume V = 45.5 dm3.

11. The volume of a frustum of a cone is V = 38 000π cm3. The radius of the lower base is 10 cm larger than the radius of the upper base.

Determine the radii of the bases, if v = 60 cm.
Solution:

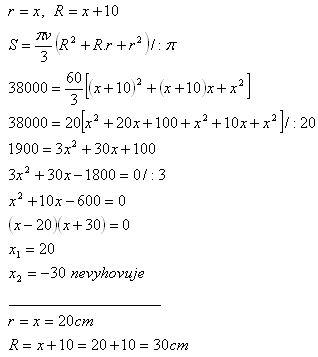
pyramid-cone-11

The radii of the bases of the frustum of the cone are R = 30 cm and r = 20 cm.

12. A frustum of a cone with radii x = 15 cm, y = 13 cm and height v = 9 cm was rolled out into a cylinder with radius r = 7.67 cm.

What is the length of this cylinder?
Solution:

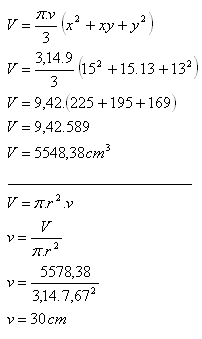
pyramid-cone-12

The length / height of the cylinder is 30 cm.