Quadrilateral

1. Characterize the quadrilaterals:

Solution:

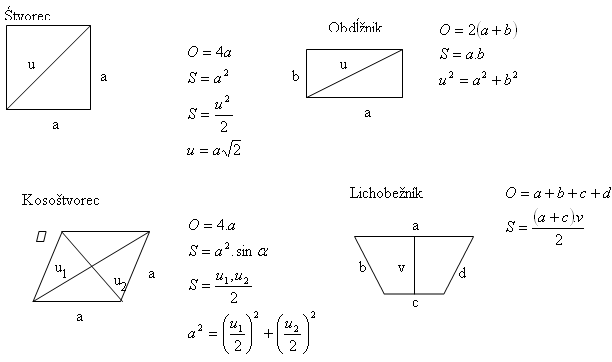
2. In a rhombus with area S = 864 cm², one diagonal is 12 cm shorter than the other.

Solution:


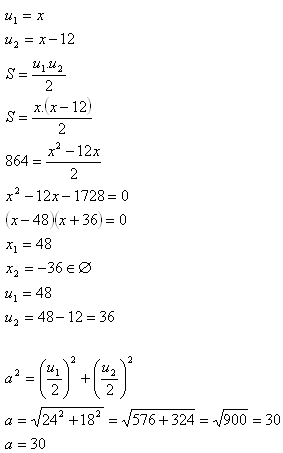
In the rhombus, the diagonals are u₁ = 48 cm, u₂ = 36 cm.
Side a = 30 cm.

3. A rectangle has a perimeter O = 46 cm and a diagonal u = 17 cm.

Solution:

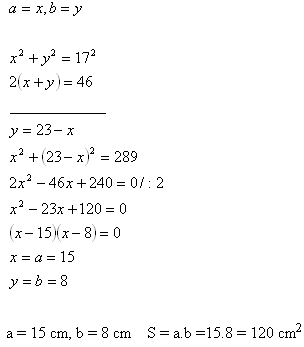
4. A rhombus has diagonals u₁ = 6 cm, u₂ = 8 cm.

Solution:

5. A regular hexagon is inscribed in a circle with radius r.

Solution:



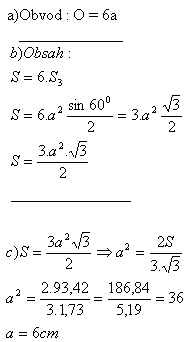
The side of the regular hexagon is a = 6 cm.

6. An isosceles trapezoid has a lower base c = 2.9 cm, height v = 7.5 cm, and angle α = 35°.

Solution:


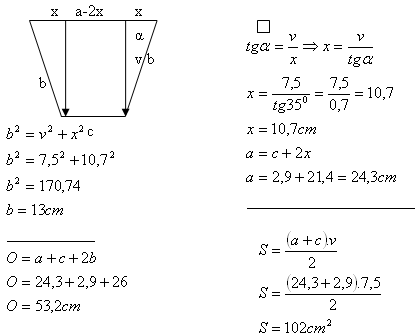
The perimeter of the isosceles trapezoid is 53.2 cm and the area is 102 cm².

7. Trapezoid ABCD has an area S = 7.2 cm², bases AB = 1.4 cm, CD = 0.6 cm.

Solution:


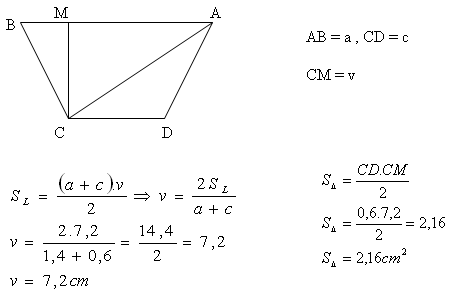
The area of triangle ΔABC is S = 21.6 cm².

8. The height and parallel sides of a trapezoid are in the ratio v:a:c = 2:3:5, and its area is S = 512 cm².

9. A rectangle has a diagonal u = 34 cm. If each of its sides is increased by 4 cm, its area increases by 200 cm².

Solution:



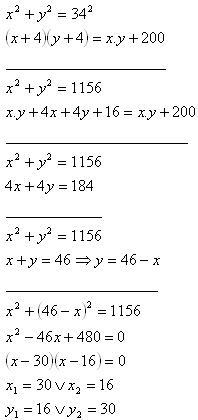
The dimensions of the rectangle are a = 30 cm, b = 16 cm.

10. A trapezoid has a top base c = 33 cm and height v = 15 cm. The other three sides are equal.

Solution:



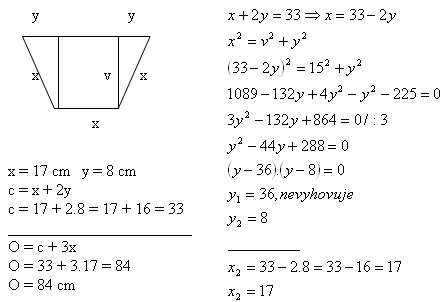
The perimeter of the trapezoid is O = 84 cm.