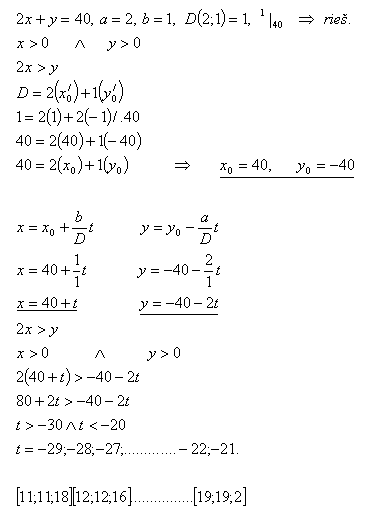Diophantine equations
1. Solve the equations:
ax + by = 0 and ax + by = c
Solution:
The Greek mathematician DIOPHANTUS (about 250 BC) dealt with solving equations of the type ax + by = c, where only integer solutions were accepted. Such equations are called “Diophantine equations”.
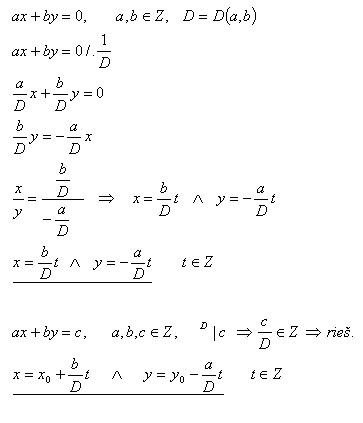
2.In the set Z solve the equation:
6x – 4y = 0
Solution:
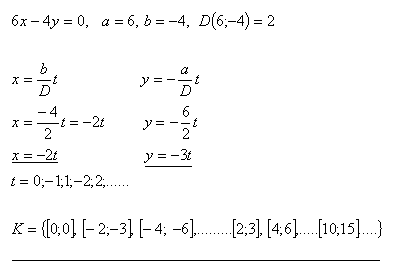
3.In the set Z solve the equation:
3x + 15y = 0
Solution:
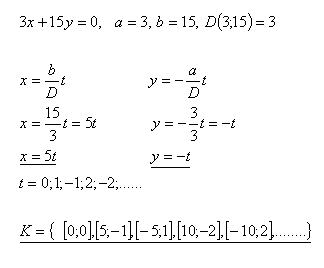
4.Find out which of the following equations are solvable in the set Z:
Solution:
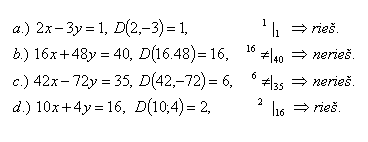
5.In the set Z solve the equation:
10x + 4y = 16
Solution:
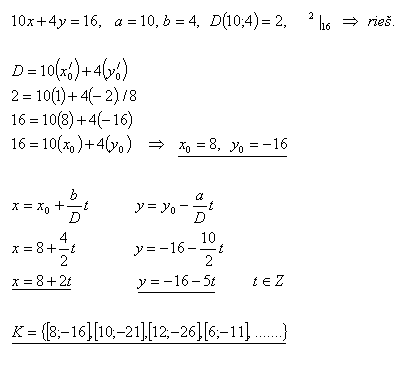
6.In the set Z solve the equation:
21x +15y = 3
Solution:
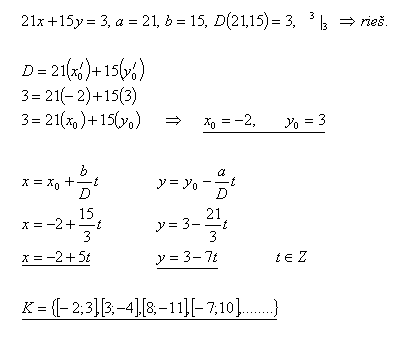
7.What integer dimensions can a rectangle have if its perimeter is 24 cm?
Solution:
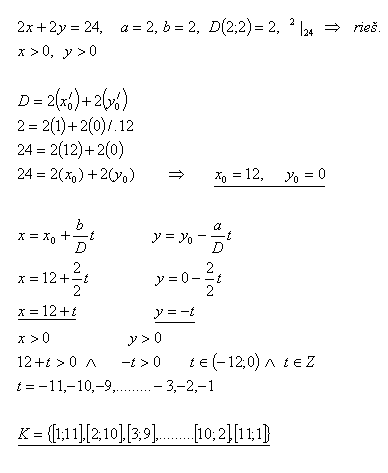
8.In what ways can you pay the sum of 21 euros if you only have 2-euro and 5-euro coins?
Solution:
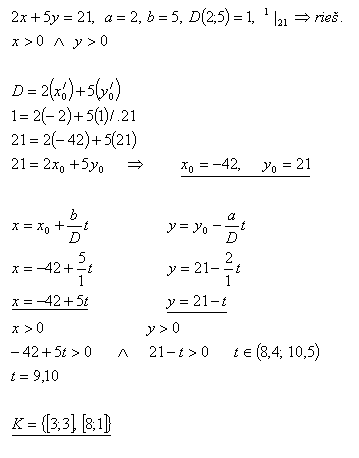
9.Determine how many ways 22 liters of wine can be transferred into 2-liter and 3-liter containers.
Solution:
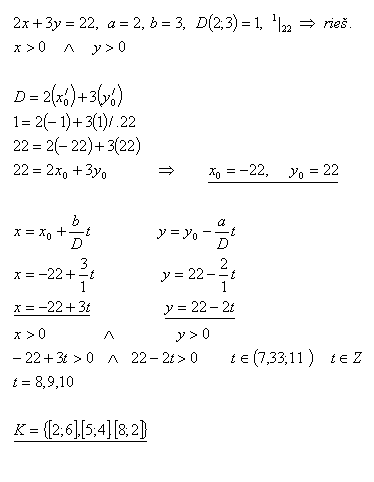
10.A ribbon 50 cm long is to be cut into pieces 6 cm and 4 cm long. In how many ways can this be done?
Solution:
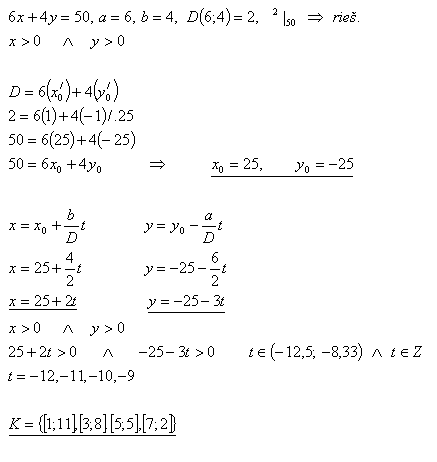
11.Determine all isosceles triangles whose side lengths are integers and whose perimeter equals 40 cm.
Solution: