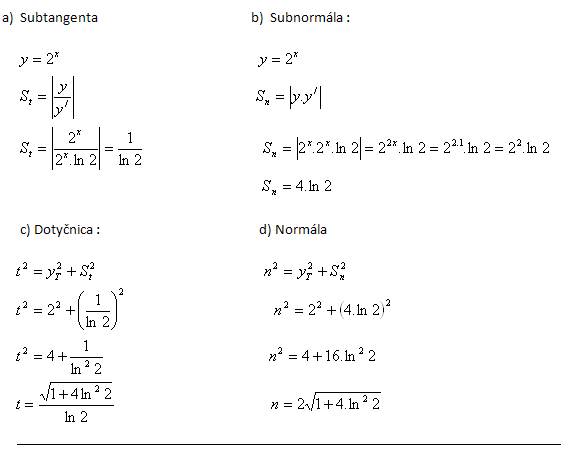Geometric meaning of derivation
1.What is the geometric meaning of the derivative?
Solution:
Using the derivative of the function y = f(x) we can write the equation of the tangent or the equation of the normal to the graph of the function at the point T [xT , yT]
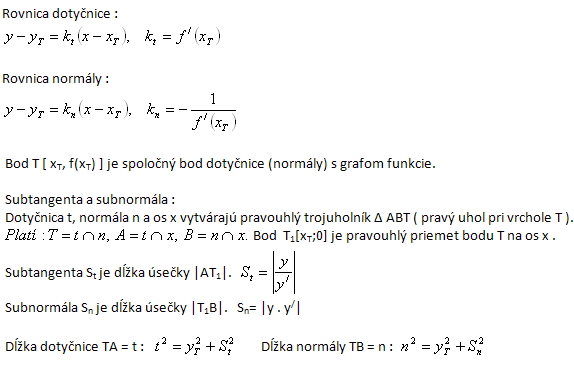
2. Write the equation of the tangent and the equation of the normal to the curve:
Solution:
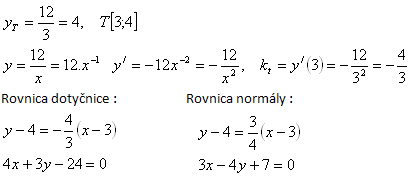
3. Write the equation of the tangent and the equation of the normal to the curve:
Solution:

4. Write the equation of the tangent and the equation of the normal to the curve:
Solution:
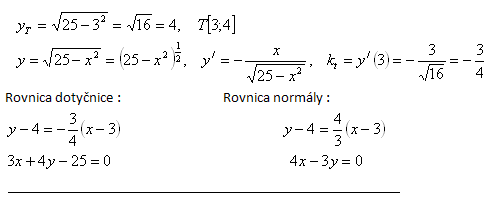
5. Write the equation of the tangent and the equation of the normal to the curve:
Solution:
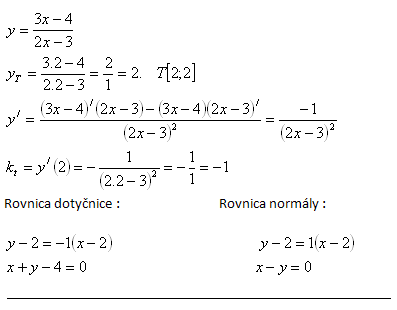
6. Write the equation of the tangent and the equation of the normal to the curve y = ln(x+1) at the point T[0; yT]
Solution:
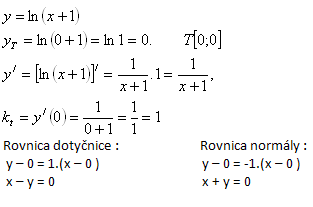
7. Write the equation of the tangent to the curve y = sin 2x at the point T [3π/4 ; yT].
Solution:
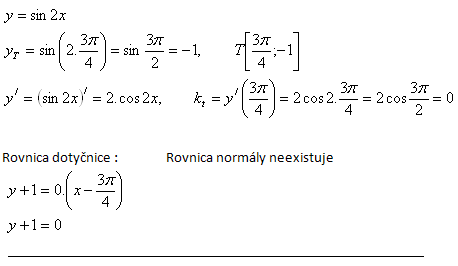
8. Write the equation of the tangent to the curve y = x2 – 4x + 3 , which makes an angle φ = 450 with the x-axis.
Solution:
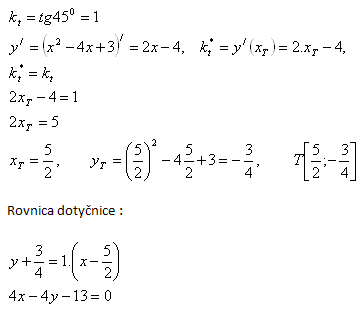
9. Find the equation of the tangent to the curve y = x2 - 2x + 3 , if the tangent is parallel to the line p : 3x - y + 5 = 0.
Solution:
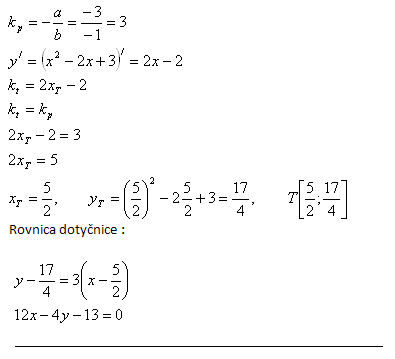
10.The function is given f : y = x3 - 9x2 + 15x + 3. Determine the contact points of the horizontal tangents.
Solution:
For horizontal tangents (parallel to the x-axis) the following holds:
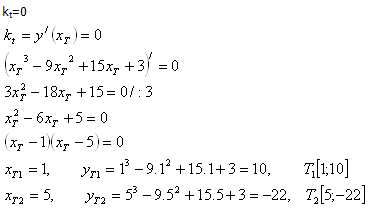
The contact points are T1[1 ; 10] and T2[5; -22]
11. Determine the angle φ between two tangents of the curve if one has contact point T1[3; yT1] and the other T2[-3; yT2]. The equation of the curve:
Solution:
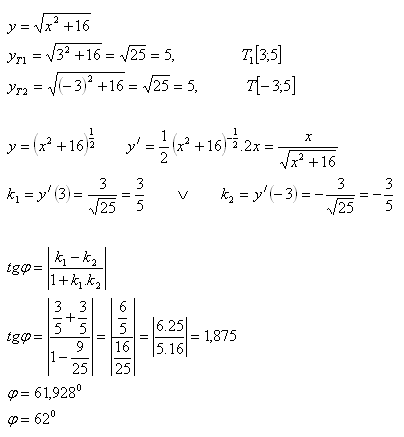
The angle between the tangents is φ = 620
12. Determine the lengths of the subtangent, subnormal, tangent and normal to the graph of the function at the point T[1; yT]. The function has the equation:
Solution:

13. Calculate the lengths of the subtangent, subnormal, tangent and normal to the graph of the function y = 2x at the point T [1; yT].
Solution:
Point T : yT = 21 = 2, T[1 ; 2 ]