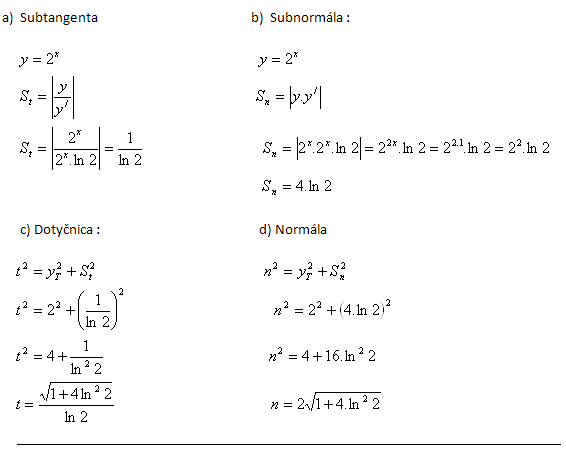Geometrický význam derivace
1.Jaký je geometrický význam derivace?
Řešení:
Pomocí derivace funkce y = f (x) můžeme napsat rovnici tečny/dotyčnice (SK) nebo rovnici normály ke grafu funkce v bodě T [xT, YT]
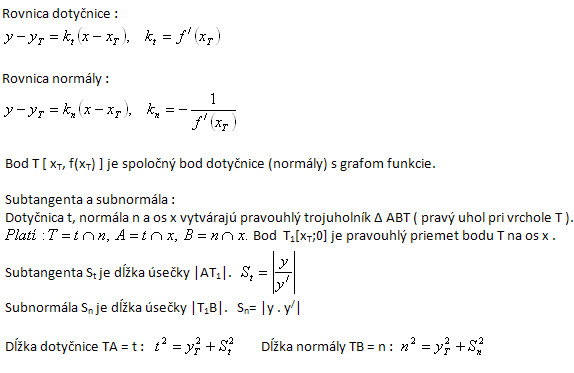
2. Napište rovnici tečny/dotyčnice (SK) a rovnici normály ke křivce:
Řešení:
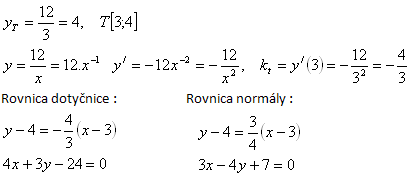
3. Napište rovnici tečny/dotyčnice (SK) a rovnici normály ke křivce:
Řešení:

4. Napište rovnici tečny/dotyčnice (SK) a rovnici normály ke křivce:
Řešení:
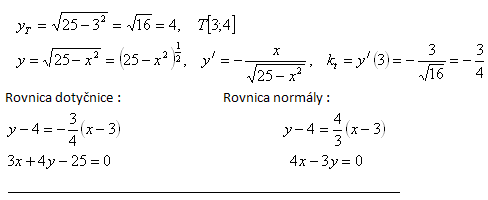
5. Napište rovnici tečny/dotyčnice (SK) a rovnici normály ke křivce:
Řešení:
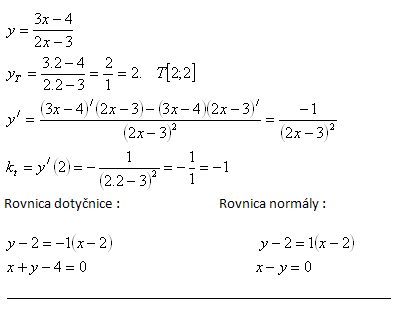
6. Napište rovnici tečny/dotyčnice (SK) a rovnici normály ke křivce y=ln(x+1) v bode T[0; yT]
Řešení:
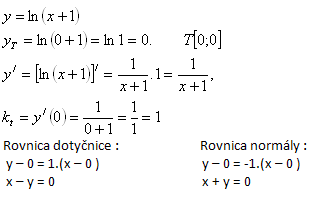
7. Napište rovnici tečny/dotyčnice (SK) ke křivce: y = sin 2x v bode T [3π/4 ;yT].
Řešení:
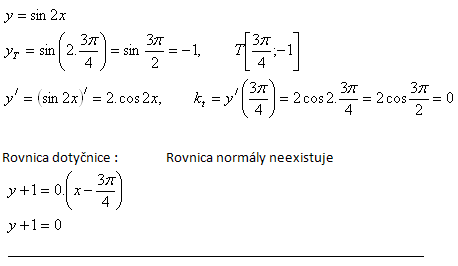
8. Napište rovnici tečny/dotyčnice (SK) ke křivce y = x2 – 4x + 3 , ktorá zviera s osou x uhol φ = 450.
Řešení:
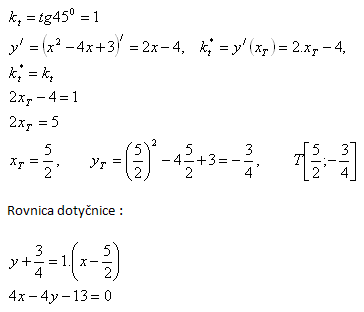
9.Napište rovnici tečny/dotyčnice (SK) ke křivce y = x2 -2x +3 , pokud tečna je rovnoběžná s přímkou p : 3x -y + 5 = 0.
Riešenie:
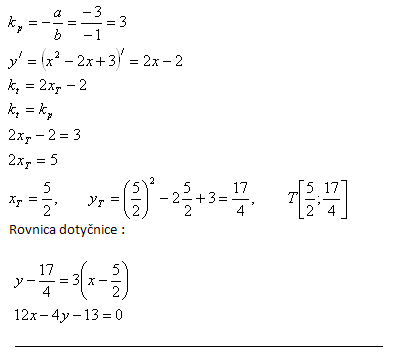
10. Je daná funkce f : y = x3- 9x2 +15x +3 . Určete dotykové body vodorovných tečen.
Řešení:
Pro vodorovné tečny (rovnoběžné s osou x) platí:
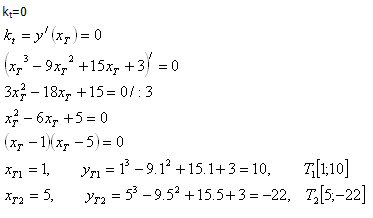
Dotykové body jsou T1[1 ; 10 ] a T2 [ 5; -22 ]
11. Určete úhel φ mezi dvěma tečnami křivky jestliže jedna má bod dotyku T1[ 3;yT1] a druhá T2[-3; yT2]. Rovnice křivky:
Řešení:
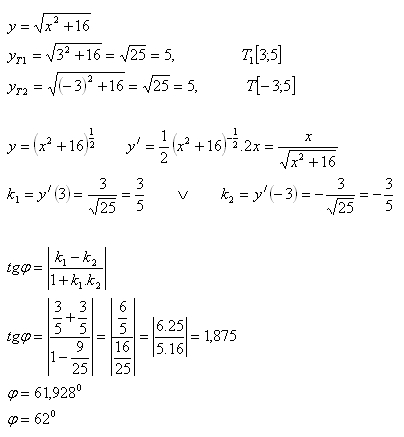
Úhel mezi tečnami je φ = 620
12. Určete délku subtangenty, subnormální, tečny a normály ke grafu funkce v bodě T [1; YT]. Funkce má rovnici:
Řešení:

13. Vypočítejte délku subtangenty, subnormální, tečny a normály ke grafu funkce y = 2x v bode T [1;yT].
Řešení:
Bod T : yT = 21= 2, T[1 ; 2 ]