Matice
1. Jaké jsou základní vlastnosti matic.
Řešení:
Obdélníková schéma m, n reálných čísel uspořádaných do m řádků an sloupců se nazývá matice (typu m, n). Pokud m = n je to čtvercová matice n - tého stupně. Čísla a11, A32, ... AMN se nazývají prvky matice.
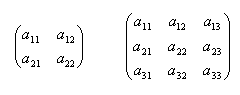
Nulová matice: Jednotková matice:
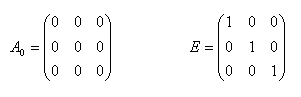
Inverzní matice A-1:
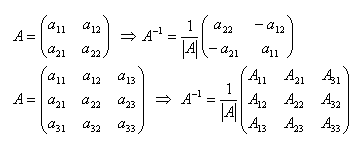
Součet matic A + B
2. Vysvětlete postup při násobení dvou matic.
Řešení:
Součin dvou matic má jen tehdy smysl, když levá matice má tolik sloupců, jak má pravá matice řádků. Takové matice se nazývají "komformabilné".
Součin matic není komutatívny!
Násobení matice číslem:
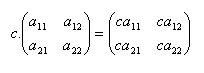
Součin matic A.B
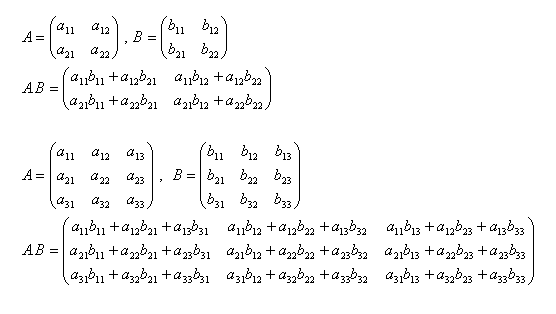
3.Sečtěte matice A + B a M + N jestliže platí
Řešení:
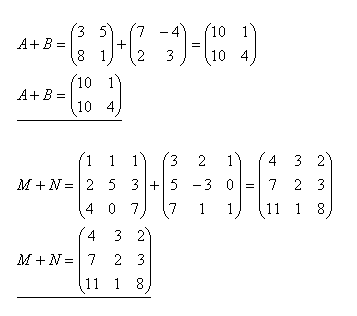
4.Vynásobte matice A.B a C.D jestliže platí:
Řešení:
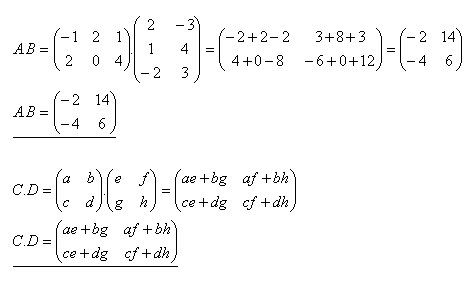
5.Ukažte, že součin matic není komutatívny.
Řešení:
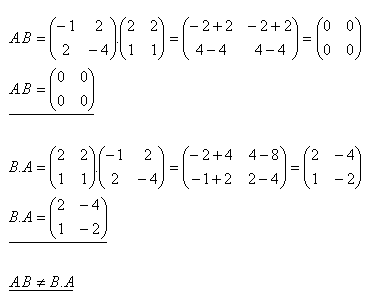
6.Daná je matice A. Zjistěte matici A2 jestliže platí:
Řešení:
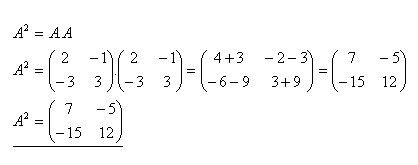
7.Daná je matice B. Zjistěte matici B2 jestliže platí :
Řešení:
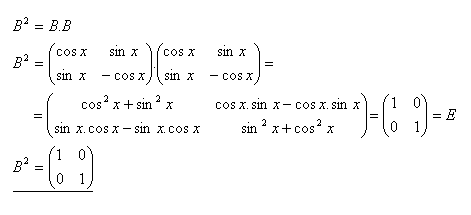
8.Zjistěte součin matic A.B jestliže platí:
Řešení:
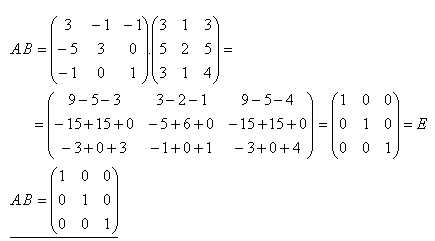
9.Vysvětlete postup při výpočtu inverzní matice A-1 z matice A.
Řešení:
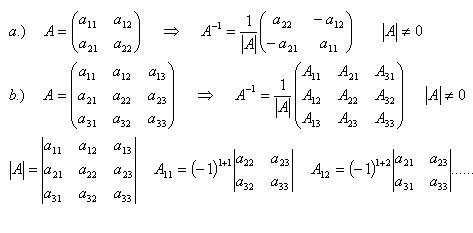
Při zkoušce musí být inverzní matice v součinu sleva.
Pro součin matic neplatí komutatívny zákon.
10.K matici A zjistěte inverzní matici A-1 a proveďte zkoušku jestliže platí:
Řešení:
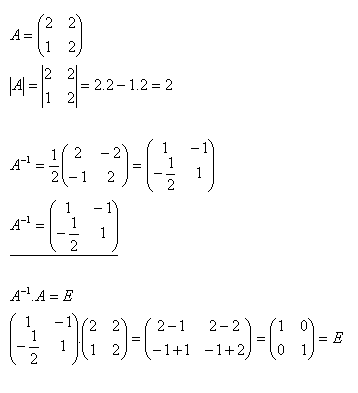
11.K matici A zjistěte inverzní matici A-1 a proveďte zkoušku pokud platí:
Řešení:
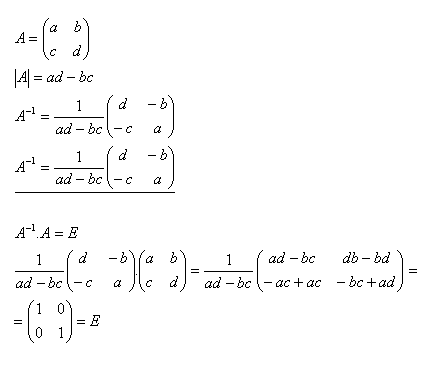
12.Vypočítejte inverzní matici A-1 k matici A, jestliže platí
Řešení:
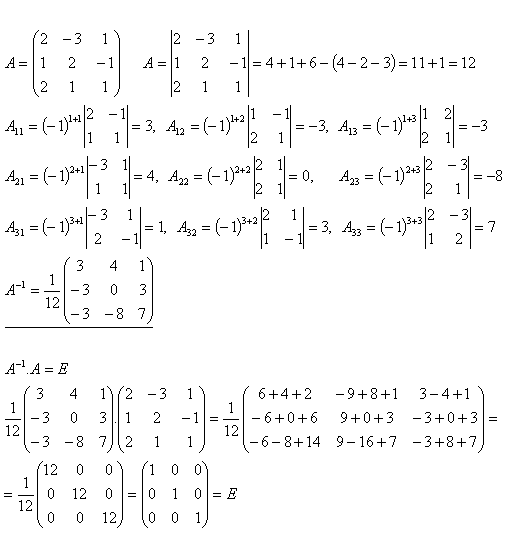
13.Vypočítejte inverzní matici A-1 k matici A a proveďte zkoušku (Viz příklad 12), jestliže platí:
Řešení:
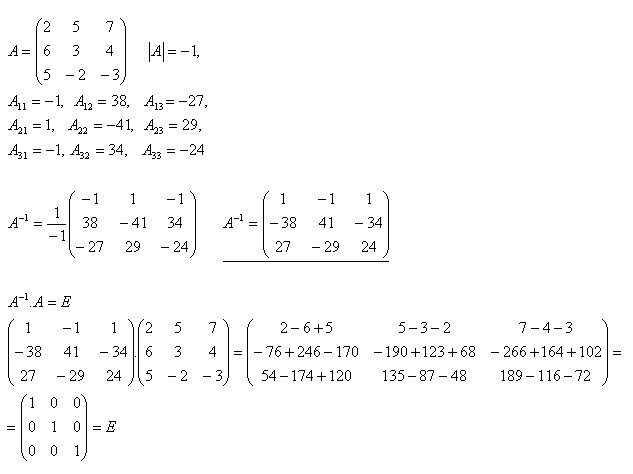
14.Řešte maticovou rovnici A + X = B pokud platí:
Řešení:
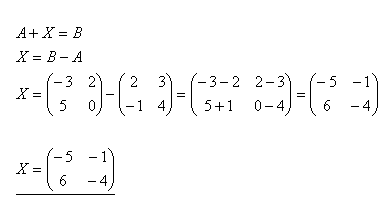
15.Vypočítejte matici X z rovnice 2A + 3X = B pokud platí:
Řešení:
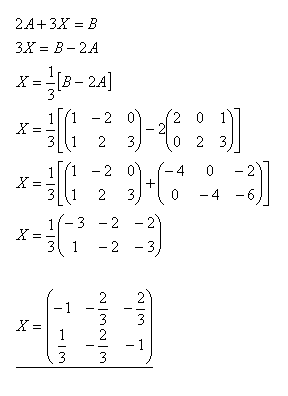
16.Řešte maticovou rovnici AX = B a proveďte zkoušku jestliže platí:
Řešení:
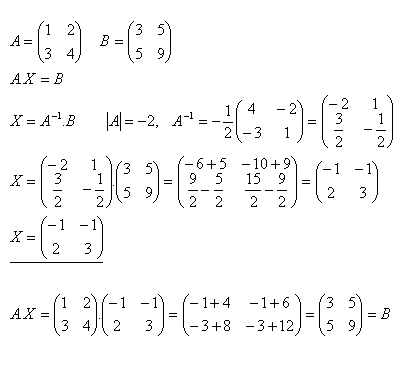
17.Řešte rovnici AX = B a proveďte zkoušku jestliže platí:
Řešení:
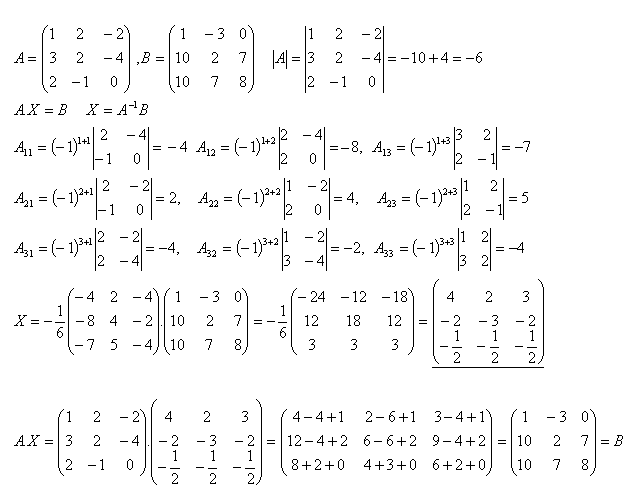
18.Vysvětlete postup při řešení soustavy lineárních rovnic pomocí inverzní matice.
Řešení:
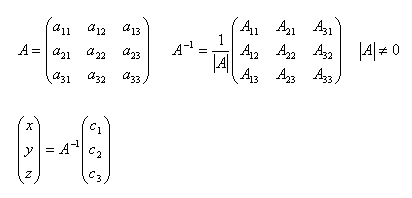
19.Pomocí inverzní matice řešte soustavu rovnic:
Řešení:
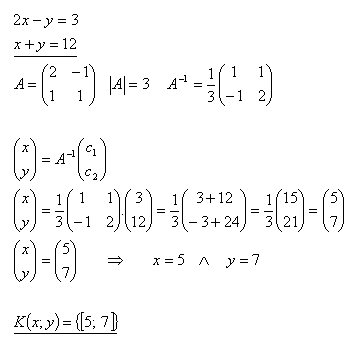
20.Pomocí inverzní matice řešte soustavu rovnic:
Řešení:
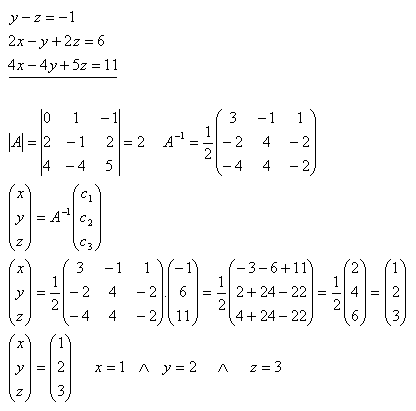
21.Pomocí inverzní matice řešte soustavu rovnic:
Řešení:
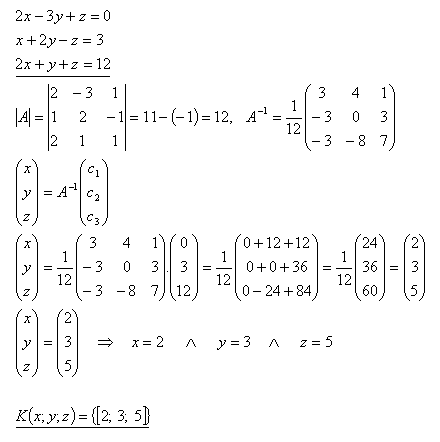
22.Pomocou inverznej matice riešte sústavu rovníc:
Řešení:
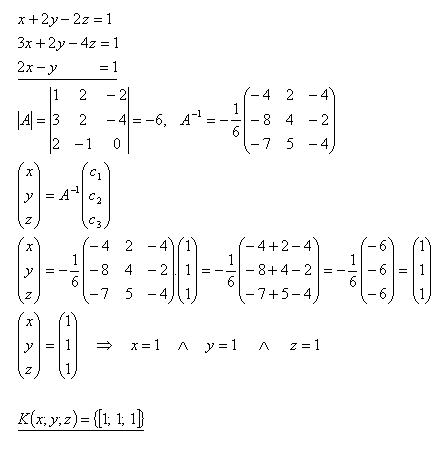
23.Vysvětlete pojem "hodnost matice" a podmínky řešení soustavy lineárních rovnic Gaussovu metodou
Řešení:
Hodnost matice h je číslo, které udává maximální počet lineárně nezávislých řádků matice. Hodnost matice se nezmění pokud:
- a.) zaměníme pořadí její řádků
- b.) libovolný řádek vynásobíme číslem různým od nuly
- c.) k libovolnému řádku přičteme jiný řádek
- d.) k libovolnému řádku přičteme lineární kombinaci jiných řádků
- e.) vynecháme řádek, který je lineární kombinací jiných řádků
- f.) vynecháme nulový řádek
- g.) vyměníme řádky za sloupce (vznikne "transponována matice")
Uvedené vlastnosti hodnosti matice platia aj pre stĺpce.
Frobeniova věta:
Soustava lineárních rovnic má pouze tehdy řešení, pokud hodnost matice soustavy h se rovná hodnosti její rozšířené matici h/.
h = h/
a.) h = h/ a h = n jediné řešení
b.) h = h/ a h<n nekonečně mnoho řešení (n je počet neznámých v soustavě)
24.Gaussovu metodou řešte soustavu rovnic:
Řešení:
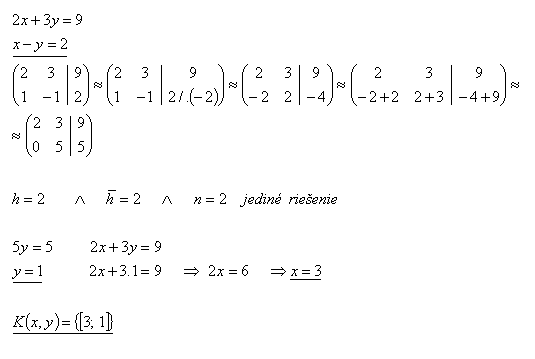
25.Řešte soustavu rovnic Gaussovu metodou:
Řešení:
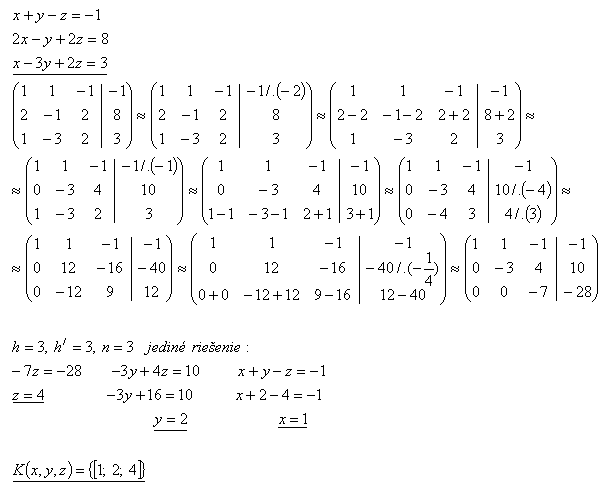
26.Řešte soustavu rovnic Gaussovu metodou:
x + 2y + 3z =0
2x – y + z = 3
3x + y – z = 5
Řešení:
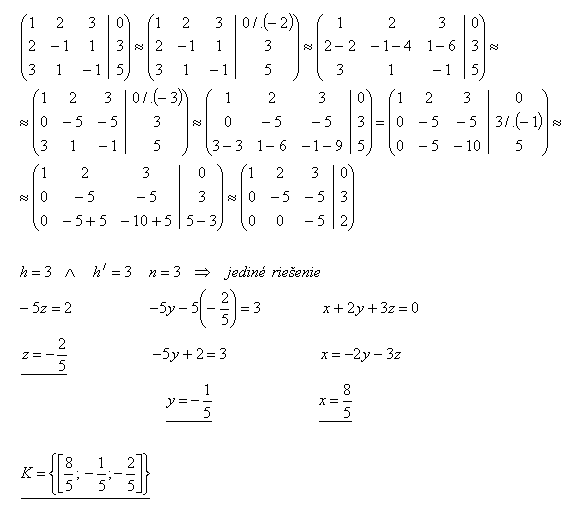
27.Řešte soustavu rovnic Gaussovu metodou:
Řešení:

Videoprezentace jsou sdílené z portálu NAUČ SA MATIKU.
⁞