Eratostenove sito
Z množiny N prirodzených čísiel možno vybrať podmnožinu, ktorá už niekoľko storočí robí matematikom starosti. Je to množina prvočísiel. Podľa definície prvočíslo je také prirodzené číslo, ktoré je deliteľné len jednotkou a sebou samým. Jednotka medzi prvočísla nepatrí. Prvým problémom je problém, ako z množiny N vybrať množinu prvočísiel. Túto otázku úspešne vyriešil ERATOSTENES z Kyrény (275 – 195 p.n.l), grécky matematik. Vypracoval metódu postupného vyraďovania zložených čísiel. Táto metóda dostala názov Eratostenove sito.
Metóda spočíva v nasledovnom:
Napíšeme si niekoľko prirodzených čísiel, napríklad 1 – 20. Jednotku vynecháme, dvojku zakrúžkujeme a každé druhé číslo od dvojky podčiarkneme. Trojku zakrúžkujeme a každé tretie číslo od trojky podčiarkneme Päťku zakrúžkujeme a každé piate číslo od päťky podčiarkneme a tak pokračujeme ďalej. Niektoré čísla budú podčiarknuté viackrát. Zakrúžkované čísla sú prvočísla.
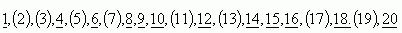
V prvej dvadsiatke prirodzených čísiel je 8 prvočísiel: 2,3,5,7,11,13,17,19. Touto metódou boli zistené prvočísla ležiace medzi 1 a 10 000 000.Usilovní počtári vypočítali všetky prvočísla z tohto intervalu a zistili, že tam je presne 664 579 prvočísiel. Prvočísla sú usporiadané v rôznych tabuľkách. Existujú tabuľky ,v ktorých na mikrofilmoch je uložených 6 miliónov prvočísiel s najväčším 104 395 301.
Literatúra: Opava, Z.: Matematika kolem nás, Praha, Albatros 1989