Rovnice roviny
1. Jakým způsobem je v prostoru určena rovina?
Řešení:
Rovina v prostoru je určena třemi různými body A, B, C, které neleží na jedné přímce.

2.Napište obecnou rovnici roviny, ve které leží bod A [-1; 5; 0]. Prochází rovina ρ počátkem souřadnic? Normálové vektor roviny je:
Řešení:
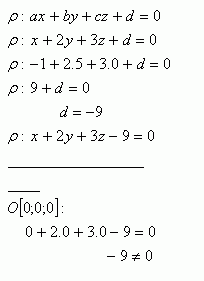
Rovina x +2y +3z -9 = 0 neprochází počátkem souřadnic.
3. V rovině ρ leží tři body A [2; -4; 5], B [3; -1; 4], C [0; -10; 7]. Napište parametrické vyjádření této roviny.
Řešení:
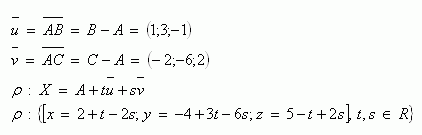
4.Rovina ρ je dána parametrickými rovnicemi. Přepište jejich do obecné rovnice roviny.
Řešení:
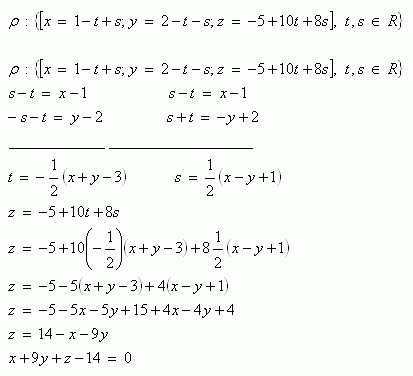
Rovnice roviny v obecném tvaru je ρ: x + 9y +z -14 = 0
5. Napište rovnici roviny σ, která prochází bodem A [3, 4, -5] a je rovnoběžná s vektory
Řešení:

6.Napište rovnici roviny, která prochází body A [2;-4;5], B [3;-1;4], C [0;1;6]
Řešení:

Rovnica roviny je 8x + y + 11z – 67 = 0
7. Napište rovnici roviny, která je dána dvěma rovnoběžnými přímkami:
Řešení:

Rovnice roviny je ρ: 2x + y -1 = 0
8.Napište obecnou rovnici roviny τ, která je rovnoběžná s osou x a prochází body A[-2;-1;-3],
B [2;3;0]
Řešení:

Rovnice roviny je τ: 3y – 4z -9 =0
9. Napište rovnici roviny π, která prochází bodem M [-4; 0; 4] a vytíná na souřadnicových osách úseky
p = 4, q = 3.
Řešení:
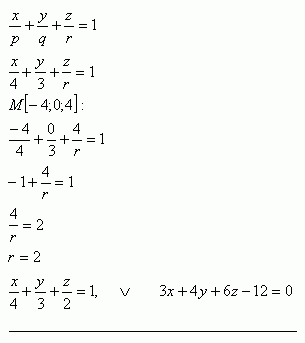
Rovnice roviny π: 3x +4y +6z -12 =0
10. Máme rovinu ρ : 2x -2y +z -6 = 0. Vypočítejte úhly její normály se souřadnicovými osami x, y, z.
Řešení:
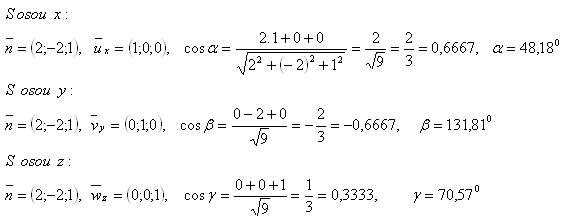
Úhly normály se souřadnicovými osami jsou: α = 48,180,β= 131,810,γ= 70,570
11.Zjistěte zda bod A [22; 2; -5] leží v rovině:
Řešení:

Bod A leží v rovině ρ.
12.Určete souřadnici "x" bodu M [x; 1,2], aby bod M ležel v rovině:
Řešení:
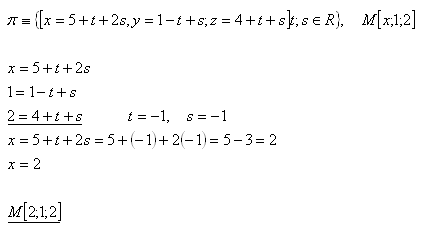
Hledaná souřadnice bodu M je x = 2. Bod M [2;1;2].
13.Napište obecnou rovnici roviny, která prochází bodem A a je kolmá na úsečku AB, jestliže platí:
Řešení:
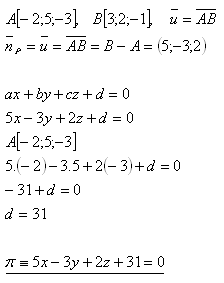
Rovnice roviny je π : 5x - 3y + 2z + 31 = 0
14.Napište obecnou rovnici roviny τ, která vytíná na souřadnicových osách úseky p = 2, q = 1, r = 5.
Řešení:
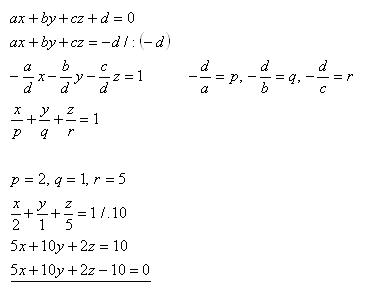
Rovnice roviny je τ : 5x + 10y +2z – 10 = 0
15.Napište rovnici roviny π, která prochází bodem M a je kolmá na přímku p. Řešte pro zadání:
Řešení:
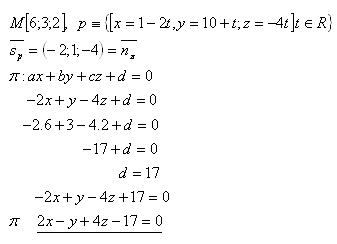
Rovnice roviny je π : 2x – y + 4z – 17=0
16.Ukažte, že body A, B, C, D leží v jedné rovině. Řešte pro:
Řešení:
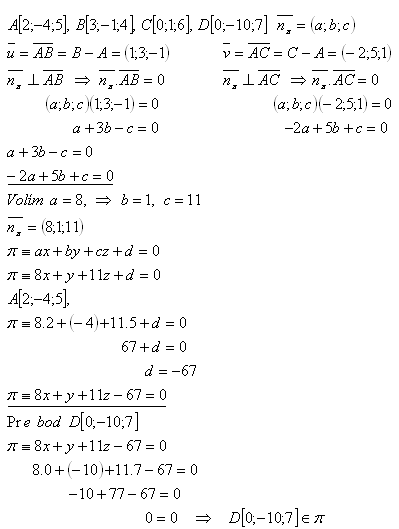
Bod D[0;-10;7] leží v rovině π. Všechny body A, B, C, D leží v rovině π.
17.Dané jsou tři kulové plochy π, τ, ρ. Napište obecnou rovnici roviny χ, která prochází středy těchto kulových ploch. platí:
Řešení:
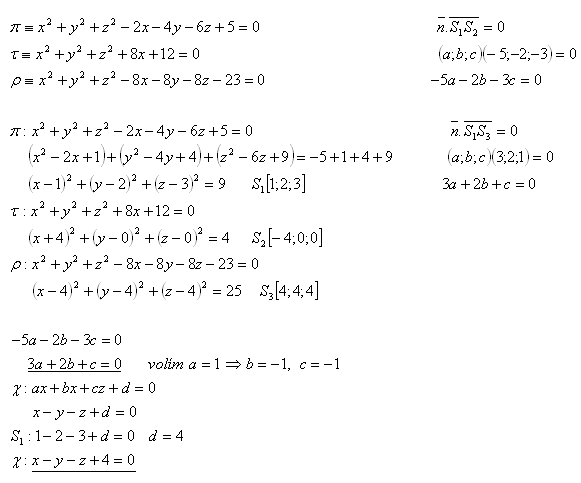
Rovnice roviny je: x – y – z +4 = 0
18.Napište obecnou rovnici roviny π, která prochází body:
Řešení:
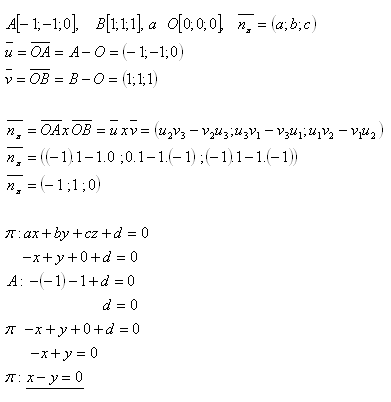
Rovnice roviny je π : x – y = 0
19.Přepište parametrický tvar roviny μ souhrnném, pokud platí:
Řešení:
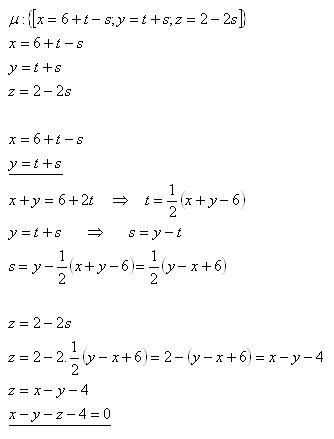
Rovnice roviny μ v obecném tvaru je μ: x – y –z – 4 = 0
20.Pro kterou hodnotu parametru "m" z množiny R leží bod M [0; 6; m] v rovině:
Řešení:
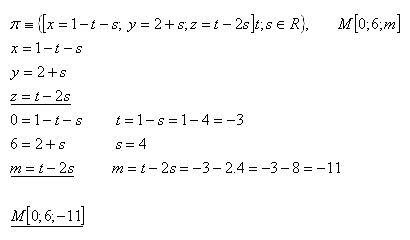
Parametr „m“ je m = –11. Bod M [0;6;-11].